ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 343
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
2) В соответствии с нашей моделью одному респонденту отвечает, вообще говоря, не одна точка, а определенное распределение точек — тех, которые отвечают суждениям, с которыми этот респондент согласен. Ведь эти суждения, вообще говоря, занимают разные места на числовой оси. "Истинная" точка, отвечающая респонденту (число, которое мы ему приписываем), это соответствующее среднее.
Заметим, что только что сформулированное положение является принципиальным: мнение любого человека о чем бы то ни было, как правило, не является точечным. Соответствующая проблема давно известна в науке. Описанное явление иногда называют плюралистичностью мнения одного респондента. Именно такой термин используется, например, в работе [Моин, 1991]. Поясним на примере более подробно, что это означает.
Пусть в качестве оцениваемого респондентами объекта выступает некоторый политический лидер. Представим себе также, что у нас имеется некий "градусник", позволяющий мгновенно измерять отношение к этому лидеру любого человека и что мы многократно "приставляем" "градусник" к некоему респонденту. Если мы будем опрашивать респондента при разных условиях, то, наверное, вообще говоря, будем получать разные результаты. При хорошем весеннем настроении и симпатичной ин-тервьюерше наш "градусник" вполне может показать завышенную оценку. Напротив, если респондента разбудит среди ночи неприятный ему интервьюер, то на "градуснике" появится показатель неоправданно низкого уровня установки. С утра респондент может весьма плохо думать о рассматриваемом политическом лидере, поскольку под руководством этого лидера в стране произошло много негативных явлений. Но, по дороге на работу почитав газету и увидев, что этот лидер, вопреки ожиданию, совершил нечто положительное с точки зрения респондента, последний приедет к месту работы с повысившимся уровнем установки. А к вечеру, поговорив с сотрудниками, респондент вполне может прийти к выводу, что радоваться нечему, и уровень его установки снова двинется вниз и т.д. Таким образом, мнение нашего респондента не будет точечным, а будет представлять собой некоторое распределение.
О плюралистичное™ мнения любого человека о чем бы то ни было нередко говорится в литературе. Но лишь в тех случаях, когда это предположение формулируется на математическом языке, на его базе удается построить конструктивные рекомендации для реализации соответствующего этапа социологического исследования.
В качестве подтверждения сказанного можно привести следующие примеры. В упомянутой выше работе [Моин, 1991] предлагается учитывать плюралистичность мнения каждого респондента. Но отсутствие строгого определения этой плюралистичное™ делает этот совет лишь благим пожеланием, не содержащим никаких элементов конструктивности. Совсем другой характер имеют рекомендации, опирающиеся на более тщательный анализ сути плюралистичное™ мнения респондента, анализ, приводящий к математическим моделям такой плюралистичное™. Примером может служить ставшая классической модель Рашевского подражательного поведения [Моделирование социальных..., 1993, с. 48—56; Рашевский, 1966], использование которой позволяет учесть влияние на установку одного респондента совокупности мнений других людей.
Тот же совет вкупе со строгим математико-статистическим определением плюралистичное™ лежит, например, в основе рекомендаций по определению выбора числа градаций, на которое следует делить диапазон изменения непрерывного признака [Орлов, 1977]). Рекомендации конструктивны, ими может воспользоваться любой социолог. Еще одним примером конструктивного подхода к определению интересующей нас плюралистичное™ и формированию на его основе практических рекомендаций является модель Терстоуна парных сравнений, рассматриваемая в п. 6.2.1.
3) Каждому суждению также соответствует не одна точка на
оси, а распределение точек — совокупность рангов, которые
приписывали суждениям эксперты. "Истинное" положение суж-
дения на оси (число, которое мы ему приписываем, вес сужде-
ния) определяется соответствующим средним.
То же распределение можно интерпретировать и по-другому, а именно можно считать, что соответствующие точки мы получаем, отмечая места тех респондентов, которые с этим суждением согласны. Чтобы оправдать такую подмену, напомним, что экспертам мы предлагали дать каждому суждению оценку, отвечающую выраженности установки у гипотетического респондента, согласного с этим суждением. Кроме того, мы предполагали, что эксперты представляют собой репрезентативную выборку из общей совокупности потенциальных респондентов.
4) Из двух предыдущих пунктов следует, что между респон-
дентами и суждениями в нашей модели имеется определенная
симметрия. Соответствующая геометрическая картина отражена на рис.
5.3. Упомянутые распределения обозначены нами горизонталь-
ными фигурными скобками.
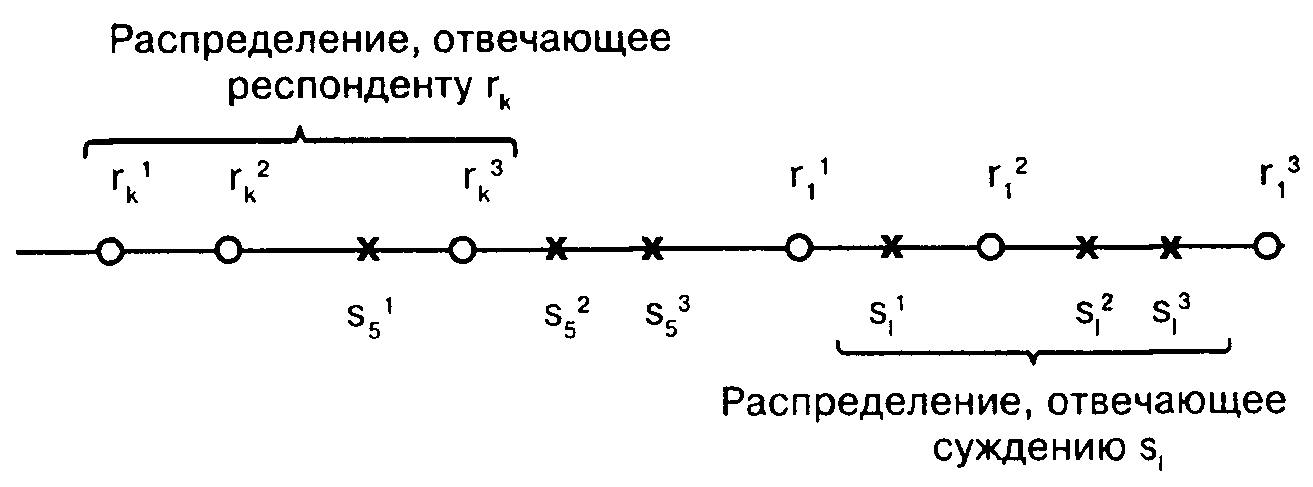
Рис. 5.3. Распределения, отвечающиеотдельнымреспондентам (о) исуждениям (х)
Итак, приписываемые респонденту гккоординаты гк', гк2, ... — это места на нашей оси тех суждений, с которыми этот респондент согласен. Приписываемые же суждению stкоординаты s/, sj1, ... означают места на оси тех респондентов, которые с этим суждением согласны. Поэтому можно сказать, что респондент представлен распределением суждений, суждение представлено распределением респондентов. Эта симметрия не случайна, так же как не было случайным то, что респонденты и суждения оказались помещенными на одну ось.
5) Поскольку место на оси каждого респондента мы находим с помощью расчета среднего значения отвечающих этому респонденту суждений, а место каждого суждения — с помощью расчета среднего значения отвечающих этому суждению (т.е. согласных с этим суждением) респондентов, то встает вопрос об обеспечении определенной однородности тех множеств, для которых упомянутые средние рассчитываются (как мы уже говорили, для неоднородных множеств вычисление среднего значения является бессмысленным). Описанная выше традиционная техника построения терстоу-новской шкалы предусматривает обеспечение однородности только для второго случая: мы отбрасываем суждения, относительно которых мнения наших экспертов (т.е. мнения согласных с этими суждениями респондентов) сильно расходятся. Но для первого случая это почему-то не делается. Представляется, что результатом может явиться неадекватность шкалы. Поясним это.
Когда респондент отмечает номера тех суждений, с которыми он согласен, разброс цен этих суждений может оказаться очень большим. Другими словами, респондент может согласиться одновременно и с суждением, имеющим цену, отвечающую резко положительной установке, и с суждением, имеющим цену, отвечающую резко отрицательной установке. В соответствии с традицией мы, не обращая на это внимания, должны рассчитывать среднее цен отмеченных респондентом суждений. Хорошо ли это? Представляется, что не очень.
Что с содержательной точки зрения может означать описанная ситуация? Очевидно, либо то, что респондент нам попался какой-то "странный", сам себе противоречащий, либо то, что наши суждения, несмотря на все наши старания, все же не отвечают тем уровням установки, которые мы для них определили. Ситуация требует глубокого социально-психологического изучения. "Странность" респондента может быть результатом того, что он не входит в ту совокупность, которую отражают отобранные нами на втором этапе эксперты. Скажем, он по-другому воспринимает какие-то суждения вследствие принадлежности к другой субкультуре. В таком случае мы должны этого респондента (вместе с такими, как он) изучать отдельно.
Ошибка в оценке суждений могла произойти, например, вследствие плохого подбора экспертов, вследствие того, что кто-то из них оказался в том же смысле "странным". В таком случае мы должны повторить процедуру, более тщательно отобрать экспертов. Может оказаться, что мы не заметили каких-то дефектов в формулировке суждений (следствием чего явилось, скажем, различие в их восприятии экспертами и нашим респондентом). Тогда мы тоже должны повторить процедуру, теперь уже переформулировав суждения, и т.д.
Но в любом случае, опросив респондента, мы должны проверить, не слишком ли сильно отличаются друг от друга по своим ценам отмеченные им суждения, т.е. должны обеспечить однородность совокупности последних.
Отметим, однако, что при определенном взгляде на природу установки большой разброс цен суждений, отмечаемых одним респондентом, может быть допустим. Имеется в виду ситуация, когда мы полагаем, что установка определяется "потенциалом напряжения", различием положительных и отрицательных эмоций респондента по отношению к объекту установки. И вполне можно допустить, что в каких-то сторонах объекта респондент видит соответствующий негатив и отмечает отрицательные суждения, а в каких-то — позитив и отмечает положительные суждения. Соответствующая медиана как бы отвечает искомому потенциалу.
5.2.3. Свойствашкалы
Возможность рассматривать оценки, полученные от разных экспертов, отвечающими одной и той же шкале
Взглянем на проблему однородности совокупности экспертов с несколько иной точки зрения. Задумаемся о том, всегда ли можно считать числа (номера ячеек), указанные разными экспертами, полученными по одной и той же шкале.
Представим себе, что один эксперт приписал какому-то суждению балл 3, а другой — балл 2. Используя в качестве способа усреднения подобных оценок соответствующую медиану, мы тем самым предполагали, что эти оценки получены по одной и той же порядковой шкале. Другими словами, мы предполагали, что, во-первых, в эмпирии существует некоторое отношение порядка, т.е. что с точки зрения одних экспертов суждение отражает больше положительных эмоций по отношению к предмету установки, чем с точки зрения других; во-вторых, это отношение адекватно отображается в числовое в процессе экспертного опроса. Применительно к указанным выше баллам это означает, ч/о второй эксперт считает наше суждение "нагруженным" более положительным отношением, чем первый. Чтобы убедиться в том, что это отнюдь не всегда отвечает истине, вспомним пример с претендентами на должность,рассмотренный нами в п. 1.2. Взглянем на рис. 1.1 и 1.2. Допустим, что они отвечают нашим первому и второму респонденту соответственно, а вместо абстрактного суждения в качестве оцениваемого объекта фигурирует претендент Ж. Несмотря на то что в первом случае Кж= 3, а во втором случае Уж= 2, совершенно ясно, что для первого респондента объект Ж более значим, чем для второго.
Нетрудно так же показать, что когда разные эксперты приписывают некоторому суждению один и тот же балл, это не обязательно означает, что они одинаково оценивают это суждение. А это значит, что наша шкала даже не номинальная. С такой шкалой вообще невозможно работать. Ситуацию можно интерпретировать как случай, когда разные эксперты оценивают суждения по разным шкалам. Естественно, для чисел, полученных по разным шкалам, мы не имеем права рассчитывать ни медиану, ни какие-либо другие параметры распределения, поскольку распределения-то как раз у нас и нет. Можно ли в таком случае сделать какое-либо модельное предположение, позволяющее "узаконить" те действия, которые предлагает Терстоун?
Подобное предположение действительно может быть сделано, и говорит оно о более глубоком понимании однородности нашей совокупности экспертов. Это предположение (явно или неявно) делается при использовании очень многих методов математической статистики. Итак, рассмотрим произвольное суждение. Вспомним, что мнение каждого человека, в том числе и эксперта, об этом суждении плюралистично, представляет собой распределение, и будем считать, что это распределение (а его у нас нет) совпадает с тем, которое мы фактически получили в результате опроса всех наших экспертов. Другими словами, будем считать, что распределение, получающееся в результате многократного опроса одного респондента, совпадает с тем распределением, которое получается в результате однократного опроса многих респондентов. Это и есть наше предположение. Нетрудно видеть, что оно действительно говорит о некоторой однородности совокупности респондентов (экспертов).