Добавлен: 26.10.2023
Просмотров: 133
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
надо перемножить и ответ сверить с дробью, записанной на листочке, на стебле. Если ответы совпадут, то цветок целебный, если нет – ядовитый. На лепестках одного цветка записаны 2/3; 0,5; 1 целая ½ (1/2);
далее 1 целая ¼; 4/5; 1,25/6 (1/4);
3,5; 1,5; 2/3 (3 целая ½)
3/5; 1 целая 2/3; 5/4; 4/5 (0,5)
0,8; 1,1; 10/11; 1 целая ¼ (1) и т.п.
У каждого ученика на парте лежат красная и зеленая карточки. Если цветок ядовитый, то поднимают красную карточку, если целебный – зеленую. Вслух ничего не произносят. Среди дробей в задании встречаются взаимно обратные. Так закрепляются правило умножения взаимно обратных чисел.
Задание 4
После цветочной поляны мы попали на перепутье. По какой дороге идти? каждый ряд должен выполнить по одному заданию, которые записаны на доске. Обязательное условие: ответ записать в виде десятичной дроби и округлить до единицы.
Ребята делают расчеты на своих местах, а трое учеников - у доски. Получаются ответы: 0,64, 0, 0,04. Ноль в ответе означает, что это тупик. Значит, надо идти по дороге№1.
Задание 5
Мы подошли к озеру. Наловим рыбки для ухи. На доске написаны пять заданий, которые закрыты листами бумаги. На учительском столе разложены пять крупных рыб, вырезанных из бумаги. На каждой рыбе проставлен номер (это номер задания). Голова рыбы унизана скрепками. Берем удочку (обычная палочка с леской, на конце лески прикреплен магнит). Магнит цепляет скрепки - и рыбка поймана. По ее номеру становится ясно, какое задание открывать для решения:
а) На какое число надо разделить 2, чтобы получить 4?
б) Меньше или больше половины литровой банки наполнился водой, если в нее
2 2
влить: — л; 0,7; — л ?
5 4
в) Вычислите:
( 5 1/5 : 3 + 0,83 * 2,16 + 7 ¼ ) 8 ( 0,5 – ½ )
г) Найдите сумму четырех десятых числа 40 и двух третей числа 36.
д) «Поудив» рыбу и сварив воображаемую уху, мы подходим к мельнице. Мельница перемалывает все написанные числа начиная с середины ( это число 4,5). Числа записаны кружочками. Пойдем и мы вслед за стрелками по спирали от одного кружка с дробью к другому, выполняя по пути то действие, которое записано на стрелке ( прибавить, перемножить и т.д. в виде значка). Например:
4,5 – 3 2/3 = 5/6 →5/6 +4 1/6 = 5 →5 – 2,7 = 2,3 …
Получив конечный ответ, отправляемся дальше. По аналогии можно подобрать множество заданий, усложнив или упростив их содержание.
Задание 6. Но тут начинается буря(учитель
включает магнитофон, и раздаются звуки сильного ветра и потоков дождя). Мы вымокли, озябли. С надеждой смотрим на карту и с радостью замечаем, что можем укрыться в пещере. А погода испортилась надолго. Сколько же мы сможем продержаться здесь? Ответ на этот вопрос мы найдем, решив задачу про пещеру, воду и проценты.
Задача. В пещере обнаружено 750 л пресной воды. На сколько дней хватит этого запаса воды для 30 человек, если один человек расходует 0,2 % от всего количества воды? Сначала разбираем решение всем классом, а затем один ученик делает записи на доске:
А) 0,2 % = 2/1000;
Б) 750:1000*2=1,5л воды расходует один человек в день;
В)1,5 *30 = 45 л воды расходуют 30 человек в день;
Г) 750:45 = 16 целых 2/3 дней будет расходоваться запас воды в пещере.
Интересно обсудить с ребятами вопрос об округлении результата. Нужно ли округлять число 16 целых 2/3? Нужно, поскольку в задаче требуется узнать целое число дней. Как округлять? Лучше рассуждать неформально. Так, если нам хватило воды на 16 полных дней и еще на две трети дня, то это значит, что в последний неполный день мы все же без воды не остались. Тогда ответ должен быть таким: воды хватит на 17 дней, то есть 2/3>1/2, тогда 16 целых 2/3 (бесконечная дробь 16,6) =17
Задание 7. Отдохнув, мы двигаемся далее. Наконец, дошли до места, где зарыт клад. Но нам преграждает путь дракон.
Плакат с нарисованным цветным драконом укреплен на обратной стороне подвижной створки доски. Каждая голова дракона держит с зашифрованным словом, где известны только первая и последняя буквы «дробь», «сложение» и «вычитание».Вот теперь наступает самая волнующая минута - можно взять клад!
И тут учитель из «тайника» достает ларец (хорошо, если это будет шкатулка, стилизованная под старину) и медленно его открывает. Напряжение растет: все видят много – много старинных монет. На самом деле это просто круглые шоколадки в золотой фольге. Дети честно делят «клад» и весело поедают свою долю.
Подведение итогов. Выставляются оценки.
Приложение 3
5 класс. Урок-путешествие "Действия с десятичными дробями"
ХОД УРОКА
1. Организационный момент.
Проконтролировать, чтобы за каждой партой сидело по одному сильному ученику. Объявить тему урока и его задачи.
Учитель: Сегодня у нас урок – путешествия в страну десятичной дроби и мы с вами отправимся в полет, и у нас будет много приключений.
2. Устная работа.
Учитель: Сначала проверим готовность к полету. Мы проверим это умение в устном счете. Вам нужно стараться отвечать правильно и быстро, от этого зависит, полетим мы в путешествие или нет.
Вопросы учащимся
1) Сформулируйте правила сложения, умножения, деления десятичных дробей?
2) Повторить распределительное свойство.
1. Прочитайте
1,1; 5,678;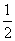
; 6,7 ;
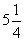; 0,001;
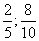; 12,003.
2. Вычислите
0,2 • 43 0,54 + 3,06 3,5 • 0,2
+ 0,4 : 0,2 +1,1
: 0,3 : 9 : 2
• 0,2 =6 -1,99 =0,01 + 0,1 = 1
3. Упрости 4,5a + 5,6a 4.
Представьте в виде десятичной дроби 2,4y – 0,2y 20%; 40%; 56%: x + 1,1x + 6,4x
Учитель: Теперь мы к полету готовы. Но нам надо узнать, на каком самолете мы должны совершить полет (По таблице нужно ответить на вопросы)
ТУ -354
4. Назовите, дробь больше 2,4 ,но меньше 3,1.
5. Округлите дробь 2,567 до сотых.
3) Самую маленькую дробь, находящуюся в промежутке от 1 до 5.
4) Дробь, в которой одна цифра повторяется несколько раз.
5) Найдите произведение чисел 0,08 и 0,5.
Т -3,05; У- 2,57; 3- 0,32; 5 – 4,8888 ; 4 – 0,4.
Учитель: Теперь мы с вами летим в самолете ТУ-354.
В самолетах обычно слушают музыку, читают газеты, разгадывают кроссворды. Итак, мы будем лететь, играть в “математическое лото”. Кто быстрее решит и зачеркнет все числа в лото тот победит? Можно решать устно.
3. Работа в тетрадях.
Учитель: Ужасно, но наш самолет терпит крушение. Пилот у нас очень хороший, поэтому он с трудом, но сажает самолет на остров. На этом острове встречаются аборигены и путешественники. Аборигены - это ребята первого варианта, а путешественники – это ребята второго варианта. Внимание кризисная ситуация, аборигены ходят уничтожить наших путешественников. Чтобы этого не произошло, путешественникам надо доказать, что они умеют выполнять действия с дробями.
Работа в парах. Ребята первого варианта контролируют выполнения заданий второго варианта.
Вычислите
(2,36 • 1,5 +24,9) • 45
(61,5 – 5,16) : 30 +5,05
4. Самостоятельная работа (10 мин).
Учитель: Аборигенам путешественники понравились. И они не только стали враждовать с ними, но и рассказали о своей цивилизации.
Путешественники и аборигены познакомились, обменялись знаниями и подружились. Для закрепления своего союза они решили сыграть в дружеский футбольный матч. Гол – это правильно решенное уравнение
1) (x – 5,6): 12 =3,7
2) 12x + 14x + 4,2 =12
3) ( x + 2,1) • 4 = 15,2
4) (9,1 – x ) – 2,8 = 2,9
5) 4,6x + 3,8x – 1,6 = 0,5
5. Физминутка.
Учитель: Потом были танцы у костра. (Под музыку повторяют движения за учителем)
6. Работа у доски.
Учитель: После матча, чтобы еще более закрепить дружбу, проводится банкет. Но чтобы устроить банкет, чтобы всем всего хватило, местные жители должны решить задачу.
Задача
Запас мяса - 42 килограмма; на стол приготовили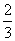
этого количества. Женщины собрали 9,2 килограммов абрикосов, а дети насобирали бананов в 1,5 раза больше. Сколько мяса и сколько фруктов на столе?
Условие задачи записываем на доске и решаем с комментированием.
7. Задачи на смекалку.
Учитель: На стол накрыли. Хорошо поужинали, при этом никого не обидели. Особо смелые перепрыгивали через костер. Для того, чтобы перепрыгнуть надо решить задание на смекалку.
Кирпич весит 2 кг и еще полкирпича. Сколько весит кирпич? (3 кг)
Пара лошадей пробежала 40 км. Сколько километров пробежала каждая лошадь? (40 км)
У семи братьев по одной сестре. Сколько всего детей? (8)
К Айболиту на прием пришли звери. Все, кроме 2, собаки. Все, кроме 2, кошки. Все, кроме 2, зайцы. Сколько животных пришло к Айболиту? (3)
Зайцы пилят бревно. Они сделали 12 распилов. Сколько получилось чурбаков? (13)
8. Решение задачи.
Учитель: Поели, поплясали, даже через костер попрыгали, пора бы и спать ложиться. Но у аборигенов свои обычаи. Пустят путешественников спать в хижину только после того, как они найдут объем жилища и площадь его потолка. Размеры у хижины такие: высота –2,5 м; длина - 6,25 м; а ширина – 5 м.
9. Подведение итогов.
Учитель: Ну, вот и наступило утро. За путешественниками прилетел вертолёт. Но в аэропорту их ждали журналисты, которые стали спрашивать, что же произошло за время полета и что повторили за время этого путешествия?
Учитель комментирует оценки за урок.
10. Домашняя работа нарисовать путешествие в страну “Дроби”.
Приложение 4
7 класс. Виды треугольников. Построение треугольников
ХОД УРОКА
I. Организационный момент.
- Ребята, встали. Здравствуйте! Садитесь. Какое сегодня число? Какой день недели? Посмотрите, все ли вы готовы к уроку?
- Хорошо. Начинаем работать. Проверим осанку.
II. Первичная актуализация имеющихся знаний.
Есть в математике молва,
Что она в порядок ум приводит,
Потому хорошие слова
Часто говорят о ней в народе.
Ты нам, математика, даёшь
Для победы важную закалку.
Учится с тобою молодёжь
Развивать и волю, и смекалку.
- Вот и сегодня продолжим развивать волю, смекалку и накапливать знания, отрабатывать умения.
Какой сейчас урок? (Геометрия)
Чем занимается наука геометрия?
Когда и где возникла эта наука?
Для чего нужны знания по геометрии? (Геометрия очень интересная и увлекательная наука)
Геометрия – это часть математики и возникла она очень давно, в древние времена. Эта наука возникла из практических потребностей человека измерить землю. Слово “геометрия” греческого происхождение, в переводе с греческого “геометрия” означает “землемерие” (гео – земля, метрео – измерять). Как наука геометрия зародилась в Древнем Египте около 2 000 лет до нашей эры, получается 4 000 лет назад. Египетский фараон разделил землю, выделил простому египнянину участок земли, за это они фараону платили налог за землю. Река Нил выходя из берегов, заливала участки, и фараон посылал землемеров (“гарпедонавтов”) установить, на сколько уменьшился участок и какой теперь брать налог. Так возникла геометрия в Египте, а оттуда перешла в другие страны.
Геометрические знания были необходимы людям во все времена для того, чтобы измерять землю, строить дома, путешествовать на кораблях. Эти знания и сейчас нужны рабочим, строителям, инженерам, лётчикам, людям других профессий. (Геометрия – это наука о различных фигурах и их расположении в пространстве)
далее 1 целая ¼; 4/5; 1,25/6 (1/4);
3,5; 1,5; 2/3 (3 целая ½)
3/5; 1 целая 2/3; 5/4; 4/5 (0,5)
0,8; 1,1; 10/11; 1 целая ¼ (1) и т.п.
У каждого ученика на парте лежат красная и зеленая карточки. Если цветок ядовитый, то поднимают красную карточку, если целебный – зеленую. Вслух ничего не произносят. Среди дробей в задании встречаются взаимно обратные. Так закрепляются правило умножения взаимно обратных чисел.
Задание 4
После цветочной поляны мы попали на перепутье. По какой дороге идти? каждый ряд должен выполнить по одному заданию, которые записаны на доске. Обязательное условие: ответ записать в виде десятичной дроби и округлить до единицы.
Ребята делают расчеты на своих местах, а трое учеников - у доски. Получаются ответы: 0,64, 0, 0,04. Ноль в ответе означает, что это тупик. Значит, надо идти по дороге№1.
Задание 5
Мы подошли к озеру. Наловим рыбки для ухи. На доске написаны пять заданий, которые закрыты листами бумаги. На учительском столе разложены пять крупных рыб, вырезанных из бумаги. На каждой рыбе проставлен номер (это номер задания). Голова рыбы унизана скрепками. Берем удочку (обычная палочка с леской, на конце лески прикреплен магнит). Магнит цепляет скрепки - и рыбка поймана. По ее номеру становится ясно, какое задание открывать для решения:
а) На какое число надо разделить 2, чтобы получить 4?
б) Меньше или больше половины литровой банки наполнился водой, если в нее
2 2
влить: — л; 0,7; — л ?
5 4
в) Вычислите:
( 5 1/5 : 3 + 0,83 * 2,16 + 7 ¼ ) 8 ( 0,5 – ½ )
г) Найдите сумму четырех десятых числа 40 и двух третей числа 36.
д) «Поудив» рыбу и сварив воображаемую уху, мы подходим к мельнице. Мельница перемалывает все написанные числа начиная с середины ( это число 4,5). Числа записаны кружочками. Пойдем и мы вслед за стрелками по спирали от одного кружка с дробью к другому, выполняя по пути то действие, которое записано на стрелке ( прибавить, перемножить и т.д. в виде значка). Например:
4,5 – 3 2/3 = 5/6 →5/6 +4 1/6 = 5 →5 – 2,7 = 2,3 …
Получив конечный ответ, отправляемся дальше. По аналогии можно подобрать множество заданий, усложнив или упростив их содержание.
Задание 6. Но тут начинается буря(учитель
включает магнитофон, и раздаются звуки сильного ветра и потоков дождя). Мы вымокли, озябли. С надеждой смотрим на карту и с радостью замечаем, что можем укрыться в пещере. А погода испортилась надолго. Сколько же мы сможем продержаться здесь? Ответ на этот вопрос мы найдем, решив задачу про пещеру, воду и проценты.
Задача. В пещере обнаружено 750 л пресной воды. На сколько дней хватит этого запаса воды для 30 человек, если один человек расходует 0,2 % от всего количества воды? Сначала разбираем решение всем классом, а затем один ученик делает записи на доске:
А) 0,2 % = 2/1000;
Б) 750:1000*2=1,5л воды расходует один человек в день;
В)1,5 *30 = 45 л воды расходуют 30 человек в день;
Г) 750:45 = 16 целых 2/3 дней будет расходоваться запас воды в пещере.
Интересно обсудить с ребятами вопрос об округлении результата. Нужно ли округлять число 16 целых 2/3? Нужно, поскольку в задаче требуется узнать целое число дней. Как округлять? Лучше рассуждать неформально. Так, если нам хватило воды на 16 полных дней и еще на две трети дня, то это значит, что в последний неполный день мы все же без воды не остались. Тогда ответ должен быть таким: воды хватит на 17 дней, то есть 2/3>1/2, тогда 16 целых 2/3 (бесконечная дробь 16,6) =17
Задание 7. Отдохнув, мы двигаемся далее. Наконец, дошли до места, где зарыт клад. Но нам преграждает путь дракон.
Плакат с нарисованным цветным драконом укреплен на обратной стороне подвижной створки доски. Каждая голова дракона держит с зашифрованным словом, где известны только первая и последняя буквы «дробь», «сложение» и «вычитание».Вот теперь наступает самая волнующая минута - можно взять клад!
И тут учитель из «тайника» достает ларец (хорошо, если это будет шкатулка, стилизованная под старину) и медленно его открывает. Напряжение растет: все видят много – много старинных монет. На самом деле это просто круглые шоколадки в золотой фольге. Дети честно делят «клад» и весело поедают свою долю.
Подведение итогов. Выставляются оценки.
Приложение 3
5 класс. Урок-путешествие "Действия с десятичными дробями"
ХОД УРОКА
1. Организационный момент.
Проконтролировать, чтобы за каждой партой сидело по одному сильному ученику. Объявить тему урока и его задачи.
Учитель: Сегодня у нас урок – путешествия в страну десятичной дроби и мы с вами отправимся в полет, и у нас будет много приключений.
2. Устная работа.
Учитель: Сначала проверим готовность к полету. Мы проверим это умение в устном счете. Вам нужно стараться отвечать правильно и быстро, от этого зависит, полетим мы в путешествие или нет.
Вопросы учащимся
1) Сформулируйте правила сложения, умножения, деления десятичных дробей?
2) Повторить распределительное свойство.
1. Прочитайте
1,1; 5,678;
; 6,7 ; ; 0,001; ; 12,003.2. Вычислите
0,2 • 43 0,54 + 3,06 3,5 • 0,2
+ 0,4 : 0,2 +1,1
: 0,3 : 9 : 2
• 0,2 =6 -1,99 =0,01 + 0,1 = 1
3. Упрости 4,5a + 5,6a 4.
Представьте в виде десятичной дроби 2,4y – 0,2y 20%; 40%; 56%: x + 1,1x + 6,4x
Учитель: Теперь мы к полету готовы. Но нам надо узнать, на каком самолете мы должны совершить полет (По таблице нужно ответить на вопросы)
ТУ -354
| 2,4 | 2,567 | 2,44 | 4,6 | 0,4 |
| 3,05 | 1,99 | 5 | 5,8 | 0,0001 |
| 1,51 | 1,36 | 3,03 | 4,8888 | 0,08 |
| 3,1 | 0,75 | 0,32 | 2,3456 | 2,4 |
| 2,001 | 2,57 | 3,7 | 5,67 | 0,5 |
4. Назовите, дробь больше 2,4 ,но меньше 3,1.
5. Округлите дробь 2,567 до сотых.
3) Самую маленькую дробь, находящуюся в промежутке от 1 до 5.
4) Дробь, в которой одна цифра повторяется несколько раз.
5) Найдите произведение чисел 0,08 и 0,5.
Т -3,05; У- 2,57; 3- 0,32; 5 – 4,8888 ; 4 – 0,4.
Учитель: Теперь мы с вами летим в самолете ТУ-354.
В самолетах обычно слушают музыку, читают газеты, разгадывают кроссворды. Итак, мы будем лететь, играть в “математическое лото”. Кто быстрее решит и зачеркнет все числа в лото тот победит? Можно решать устно.
| 50% от 2,2 |  | 7,86x – 2,86x, если x = 0,4 | 28,53 • 0,8+1,47• 0,8 | 0,8•5,6•5 |
| 1,1 | 0,1 | 2 | 24 | 22,4 |
3. Работа в тетрадях.
Учитель: Ужасно, но наш самолет терпит крушение. Пилот у нас очень хороший, поэтому он с трудом, но сажает самолет на остров. На этом острове встречаются аборигены и путешественники. Аборигены - это ребята первого варианта, а путешественники – это ребята второго варианта. Внимание кризисная ситуация, аборигены ходят уничтожить наших путешественников. Чтобы этого не произошло, путешественникам надо доказать, что они умеют выполнять действия с дробями.
Работа в парах. Ребята первого варианта контролируют выполнения заданий второго варианта.
Вычислите
(2,36 • 1,5 +24,9) • 45
(61,5 – 5,16) : 30 +5,05
4. Самостоятельная работа (10 мин).
Учитель: Аборигенам путешественники понравились. И они не только стали враждовать с ними, но и рассказали о своей цивилизации.
Путешественники и аборигены познакомились, обменялись знаниями и подружились. Для закрепления своего союза они решили сыграть в дружеский футбольный матч. Гол – это правильно решенное уравнение
1) (x – 5,6): 12 =3,7
2) 12x + 14x + 4,2 =12
3) ( x + 2,1) • 4 = 15,2
4) (9,1 – x ) – 2,8 = 2,9
5) 4,6x + 3,8x – 1,6 = 0,5
5. Физминутка.
Учитель: Потом были танцы у костра. (Под музыку повторяют движения за учителем)
6. Работа у доски.
Учитель: После матча, чтобы еще более закрепить дружбу, проводится банкет. Но чтобы устроить банкет, чтобы всем всего хватило, местные жители должны решить задачу.
Задача
Запас мяса - 42 килограмма; на стол приготовили
этого количества. Женщины собрали 9,2 килограммов абрикосов, а дети насобирали бананов в 1,5 раза больше. Сколько мяса и сколько фруктов на столе?Условие задачи записываем на доске и решаем с комментированием.
7. Задачи на смекалку.
Учитель: На стол накрыли. Хорошо поужинали, при этом никого не обидели. Особо смелые перепрыгивали через костер. Для того, чтобы перепрыгнуть надо решить задание на смекалку.
Кирпич весит 2 кг и еще полкирпича. Сколько весит кирпич? (3 кг)
Пара лошадей пробежала 40 км. Сколько километров пробежала каждая лошадь? (40 км)
У семи братьев по одной сестре. Сколько всего детей? (8)
К Айболиту на прием пришли звери. Все, кроме 2, собаки. Все, кроме 2, кошки. Все, кроме 2, зайцы. Сколько животных пришло к Айболиту? (3)
Зайцы пилят бревно. Они сделали 12 распилов. Сколько получилось чурбаков? (13)
8. Решение задачи.
Учитель: Поели, поплясали, даже через костер попрыгали, пора бы и спать ложиться. Но у аборигенов свои обычаи. Пустят путешественников спать в хижину только после того, как они найдут объем жилища и площадь его потолка. Размеры у хижины такие: высота –2,5 м; длина - 6,25 м; а ширина – 5 м.
9. Подведение итогов.
Учитель: Ну, вот и наступило утро. За путешественниками прилетел вертолёт. Но в аэропорту их ждали журналисты, которые стали спрашивать, что же произошло за время полета и что повторили за время этого путешествия?
Учитель комментирует оценки за урок.
10. Домашняя работа нарисовать путешествие в страну “Дроби”.
Приложение 4
7 класс. Виды треугольников. Построение треугольников
ХОД УРОКА
I. Организационный момент.
- Ребята, встали. Здравствуйте! Садитесь. Какое сегодня число? Какой день недели? Посмотрите, все ли вы готовы к уроку?
- Хорошо. Начинаем работать. Проверим осанку.
II. Первичная актуализация имеющихся знаний.
Есть в математике молва,
Что она в порядок ум приводит,
Потому хорошие слова
Часто говорят о ней в народе.
Ты нам, математика, даёшь
Для победы важную закалку.
Учится с тобою молодёжь
Развивать и волю, и смекалку.
- Вот и сегодня продолжим развивать волю, смекалку и накапливать знания, отрабатывать умения.
Какой сейчас урок? (Геометрия)
Чем занимается наука геометрия?
Когда и где возникла эта наука?
Для чего нужны знания по геометрии? (Геометрия очень интересная и увлекательная наука)
Геометрия – это часть математики и возникла она очень давно, в древние времена. Эта наука возникла из практических потребностей человека измерить землю. Слово “геометрия” греческого происхождение, в переводе с греческого “геометрия” означает “землемерие” (гео – земля, метрео – измерять). Как наука геометрия зародилась в Древнем Египте около 2 000 лет до нашей эры, получается 4 000 лет назад. Египетский фараон разделил землю, выделил простому египнянину участок земли, за это они фараону платили налог за землю. Река Нил выходя из берегов, заливала участки, и фараон посылал землемеров (“гарпедонавтов”) установить, на сколько уменьшился участок и какой теперь брать налог. Так возникла геометрия в Египте, а оттуда перешла в другие страны.
Геометрические знания были необходимы людям во все времена для того, чтобы измерять землю, строить дома, путешествовать на кораблях. Эти знания и сейчас нужны рабочим, строителям, инженерам, лётчикам, людям других профессий. (Геометрия – это наука о различных фигурах и их расположении в пространстве)