Файл: Для заданной схемы электропередачи определить запас статической.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 27.10.2023

Просмотров: 391

Скачиваний: 6

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

  1. Для заданной схемы электропередачи определить запас статической
устойчивости по идеальному пределу передаваемой мощности припередаче от генератора в систему мощности, равной 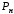,для следующих случаев:1.1. Генератор не имеет автоматических регуляторов возбуждения (АРВ) без учета явнополюсности ( 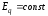–ТГ).1.2. Генератор снабжен АРВ пропорционального типа ( 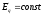). 1.3. Генератор снабжен АРВ сильного действия ( ).

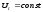  1. Построить векторную диаграмму генератора в исходном режиме.

  2. Выполнить расчет динамической устойчивости системы при трехфазном КЗ в заданной точке К при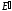 =const в следующей последовательности:
3.1. Рассчитать и построить угловые характеристики мощности нормального режима, аварийного режима и режима после ликвидации аварии.3.2. Определить угол отключения трехфазного КЗ и критический угол выбега ротора генератора.3.3. Определить коэффициент запаса динамической устойчивости.3.4. В случае нарушения устойчивости определить предельные угол и время отключения трехфазного КЗ, необходимые для сохранения устойчивости.4. Определить предельную передаваемую мощность для сохранения динамической устойчивости при отключении одной цепи двухцепной линии.5. Проверить, будет ли статически устойчива типовая нагрузка после отключениявыключателяВ схемы и определить коэффициент запаса устойчивости по напряжению в случаях отсутствия АРВ у генератора и наличии АРВ пропорционального типа и АРВ сильного действия .

  1. Определить допустимое время перерыва электроснабжения по условиям динамичской устойчивости (самозапуска)эквивалентной асинхронной нагрузки.
Примечание:

  1. Расчеты производить в относительных единицах при приближенном
приведении.Таблица 2.1Характеристики элементов электропередачи

Вариант
Генератор
Линия
Трансформаторы
Асинхронная нагрузка

SН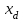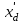




Tj
l
Uн,
Т1
Т2
РН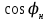


Скольжение
Tjн




(МВּА)
о.е.
о.е.
с
км
кВ
SН

(МВּА)
Uк

%
SН

(МВּА)
Uк%
МВт
о.е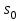


c

7
235
1,88
0,27
8,0
60
220
250
11,0
2х125
10,5
150
0,87
0,018
4

Вариант
8

Длительность КЗ
0,2
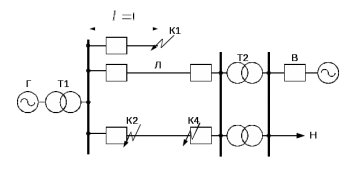
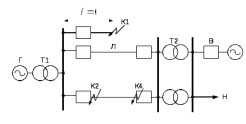
Рис. 2.1 – Схема электропередачиГ– генератор (тип, , , , ,);

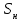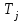Т1, Т2– трансформаторы ( , ,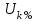 схема соединения);

Л– линия электропередачи, двухцепная со стальным тросом (l–длина, индуктивное сопротивление линии прямой и обратной последовательности 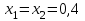Ом/км, нулевой последовательности 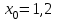Ом/км);Н–нагрузка (вид, 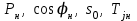); С – система бесконечной мощности; К1 – К4 – точки короткого замыкания (КЗ).Вариант -7(8)-К2.

  1. Для заданной схемы электропередачи определить запас статической
устойчивости по идеальному пределу передаваемой мощности припередаче от генератора в систему мощности, равной ,для следующих случаев:1.1. Генератор не имеет автоматических регуляторов возбуждения (АРВ) без учета явнополюсности ( –ТГ).1.2. Генератор снабжен АРВ пропорционального типа ( ). 1.3. Генератор снабжен АРВ сильного действия ( ).Составление схемы замещения и расчет параметровПри ориентировочных расчетах параметры всех схем представляются индуктивными сопротивлениями, т.е. 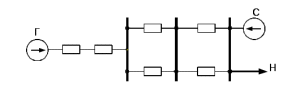простейшими однороднымисхемами замещения.Рис. 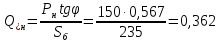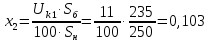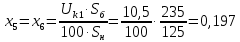3.2 – Схема замещения вариантаSб = Sн = 235 МАВ, Uб = Uн = 220 кВ, Uн* = 1, L= 60 кмР*н = Рн/Sб = 150/235 = 0,64, Х3= Х4 = ХЛ = Худ*L*Sб/Uн2 = 0,4*60*235/2202 = 0,117Iн = Рн/(Sб*cosφ) = 150/(235*0,87) = 0,734Сворачиваем расчетную схему и получаем сопротивление системы.Хс = Х2 + Х3//Х4 + Х5//Х6 = 0,103+0,117/2+0,197/2 = 0,263.3 Расчет исходного установившегося режима
При расчетах, в зависимости от типа генератора, отсутствия или наличия автоматического регулирования возбуждения (АРВ), а также способа регулирования, генератор представляется в схеме замещения индуктивным сопротивлением 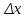и приложенной за ним электродвижущей силой (эдс) 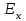. Величина сопротивления и эдс тем меньше, чем «сильнее» регулирование. Так, при отсутствии АРВ:– 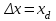; 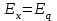– синхронные сопротивление и эдс по продольной оси;При регуляторах пропорционального типа:– 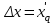; 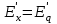– переходные сопротивление и эдс.При регуляторах сильного действия:- 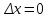; 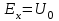– напряжение генератора.Эти величины считаются постоянными и не зависящими от режима. Положение указанныхэдс на векторной диаграмме приведено на рис. 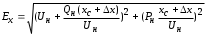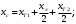3.3.Определение величины ЭДС может производиться по формуле , (3.5)где: 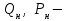значения реактивной и активной мощностей нагрузки в исходном режиме. Внутренние углы, характеризующие сдвиг вектора соответствующей ЭДС 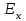относительно вектора напряжения 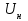( 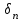,,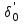 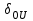), определяются по формуле 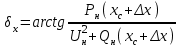. (3.6) Продольная составляющая переходнойэдс– 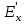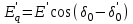. (3.7)Для построения векторной диаграммы необходимо определить все характеризующие ее величины и положение этих величин на плоскости в координатах d, q. Векторная диаграмма строится в масштабе.
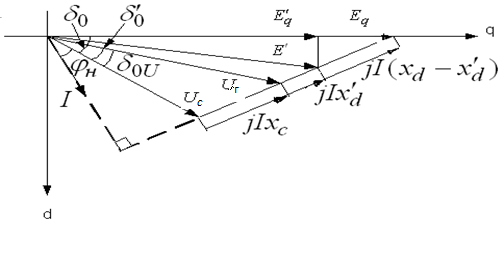
3.3.Векторная диаграмма неявнополюсного генератора (турбогенератор)Пример 2–Расчет исходного режима вариантаПо формуле (3.5) рассчитываем эдс, а внутренние углы, характеризующие сдвиг вектора соответствующей эдс относительно вектора напряжения –( ,, ) определяется согласно формуле (3.6).

  1. Без АРВ– ; .
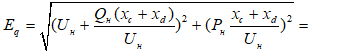
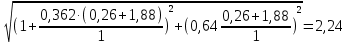
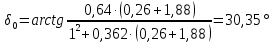
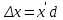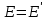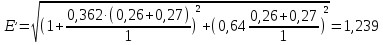
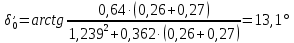
= При АРВ пропорционального действия; ; :Продольная составляющая переходной эдс: = 1,239*cos(30,35⁰-13,1⁰) = 1,183

  1. При наличии АРВ сильного действия– ; :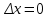
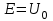U0 = 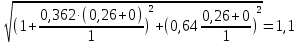1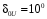 .Результаты расчетов эдс и внутренних углов( 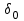,, ) между

Смотрите также файлы