Файл: Для заданной схемы электропередачи определить запас статической.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 27.10.2023
Просмотров: 128
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
и напряжением 
векторной диаграммы приведены в табл. 3.1.
Для построения векторной диаграммы определяются падения напряжения:
JXc Iн = 0,26*0,734 = 0,191
JXd/ Iн = 0,27*0,734 = 0,198
J(Xd-Xd)/ Iн = (1,88-0,27)*0,734 = 1,182
По данным расчета в масштабе строится векторная диаграмма, как представлено на рис. 3.3.
Таблица 3.1
Результаты расчетов
4РАСЧЕТ СТАТИЧЕСКОЙ УСТОЙЧИВОСТИ СИСТЕМЫ
4.1 Устойчивость простейшей электрической системы
иидеальный предел мощности
При ориентировочных расчетах (п. 1.1–1.3задания) предполагается, что устройства АРВ безынерционны и обеспечивают отсутствие самораскачивания. Предел передаваемой мощности определяется по максимуму статической угловой характеристики мощности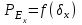
. Действие регуляторов возбуждения отражается введением соответствующих эдс
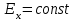, приложенных за индуктивным сопротивлением
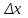. Устойчивая часть угловой характеристики мощности определяется прямым критерием статической устойчивости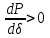
[1-3].Коэффициент запаса статической устойчивости по мощности
(
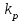)определяется как 
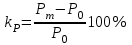. (4.1)
При определении запаса статической устойчивости нерегулируемой системы без учета явнополюсностигенератор представляется в схеме замещения синхронным индуктивным сопротивлением по продольной оси
и приложенной за ним синхронной эдс
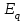Угловая характеристика мощности имеет вид
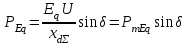, (4.2)
где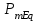
–идеальный предел мощности нерегулируемой передачи,
.
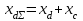Идеальный предел передаваемой мощности при наличии АРВ пропорционального действия определяется приближенно [2] без учета явнополюсности для обоих типов генераторов пр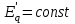и
и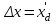
:
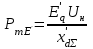. (4.3)
При АРВ сильного действия (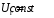
,
)
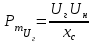. (4.4)
По результатам проведенных расчетов необходимо сделать выводы о влиянии различных факторов на запас статической устойчивости. Величина запаса статической устойчивости в нормальном режиме должна быть не меньше 20%.
Пример 3–Расчет запаса статической устойчивости
=
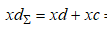=1,88 + 0,26 = 2,14
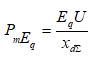
= 2,24*1/2,14 = 1,047
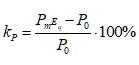
= (1,047-0,64)/0,64*100 = 63,59%
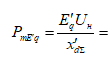
= 1,183*1/(0,26+0,27) = 2,232
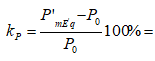
= (2,232-0,64)/0,64*100 = 249%
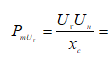
= (1,11*1)/0,26 =4,27
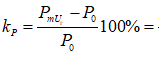
= (4,26-0,64)/0,64*100 = 566%
Результаты расчетов сведены в таблицу 4.1
Таблица 4.1
Результаты расчетов коэффициентазапаса статической устойчивости по мощности
5.РАСЧЕТ ДИНАМИЧЕСКОЙ УСТОЙЧИВОСТИ СИСТЕМЫ
5.1 Общие положения
Анализ динамической устойчивости основан на решении дифференциального уравнения относительного движения ротора и применении правила площадей. При упрощенных расчетах динамической устойчивости делаются следующие основные допущения [1, 2]:
– активная мощность первичного двигателя (турбины) остается неизменной
В течение всего переходного процесса;
– электрическая мощность, вырабатываемая генератором, изменяется мгно-
венно при изменении схемы передачи вследствие КЗ или коммутации;
– не учитываются апериодические моменты, обусловленные потерями
мощности.
Дифференциальное уравнение относительного движения ротора с учетом допущений для простейшей схемы передачи может быть записано в виде [1, 2]
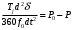
, (5.1)
где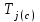
–постоянная инерции; t(c) – время;f0 – 50 Гц; (эл. градус);
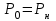– мощность турбины (нагрузки).
Электрическая мощность генератора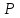
без учета явнополюсности определяется по динамической угловой характеристике мощности
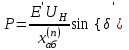. (5.2) Здесь 
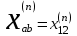– взаимное сопротивление между точкой приложения эдс
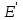и шинами системы с
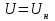для состояния (n) схемы.В дальнейшем принимаем 
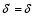. Вторая производная углового пути по времени 
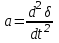является ускорением.
Текущее состояние (n) схемы включает нормальное, аварийное состояние,
определяемое видом аварии, и послеаварийное.
Критерием динамической устойчивости синхронных машин является правило (способ) площадей.м Устойчивость сохраняется в случае, если энергия возможного торможения больше энергии ускорения. Геометрическим аналогом энергии являются соответствующие площадки, построенные на основе угловых характеристик мощности (рис. 5.1) при этом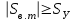
.
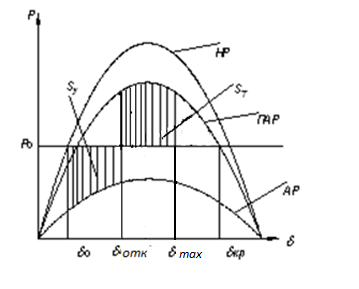
Рис. 5.1 – Применение правила площадей
На рис. 5.1
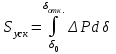
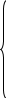; – площадка ускорения;
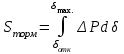–площадка торможения (5.3)
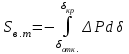–площадка возможного торможения,
где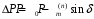
.
При трехфазном коротком замыкании на сквозной передаче электромагнитная мощность падает до нуля (Рис.5.2).
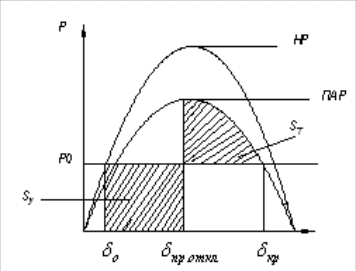
Рис.5.2 –Угловые характеристики мощности при трехфазном КЗ
При этом должны быть равны между собой площадки, соответствующие избыточным кинетическим энергиям ускорения и торможенияДля критического случая предельный угол отключениятрехфазного КЗ[1]
при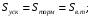
В выражении (5.4) углы выражаются в радианах (1радиан
).
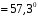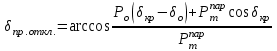. (5.4)
Здесь:
,
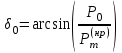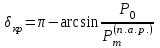
начальный и критический, с точки зрения сохранения устойчивости угол.
, 
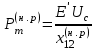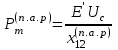
амплитуды угловых характеристик мощности исходного (нормального) и послеаварийного режимов соответственно.
, 
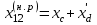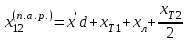
взаимные сопротивления нормального и послеаварийного режимов соответственно.
Трехфазное КЗ в точкахК1, К2 и К4 эквивалентно разрыву передачи, и на время КЗ можно получить аналитическое решение дифференциального уравнения 5.1 дающее выражение для закона изменения угла
во времени
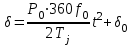. (5.5)
Возрастание угла происходит по квадратичной параболе, а предельное
время, отвечающее предельному значению угла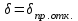
или tпр.отк, находится из уравнения 5.5
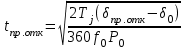с. (5.6)
В выражениях (5.5)-(5.6) углы выражаются в градусах, а постоянная времени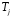
и время 
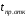в секундах, 
.
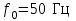Анализ динамической устойчивости методом площадей в СРС используется для вычисления коэффициента запаса динамической устойчивости, определения предельного угла отключения короткого замыкания и определения предельной передаваемой мощности при отключении одной цепи двухцепной линии электропередачи.
векторной диаграммы приведены в табл. 3.1. Для построения векторной диаграммы определяются падения напряжения:
JXc Iн = 0,26*0,734 = 0,191
JXd/ Iн = 0,27*0,734 = 0,198
J(Xd-Xd)/ Iн = (1,88-0,27)*0,734 = 1,182
По данным расчета в масштабе строится векторная диаграмма, как представлено на рис. 3.3.
Таблица 3.1
Результаты расчетов
| Вид регулирования |  |  |  |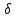
| Без АРВ | Δx = 1,88 | Eq = 2,24 | δ0 =30,35 |
| с АРВ ПД | Δx =0,27 | Eq/= 1,183 | δ0 =13,1 |
| с АРВ СД | 0 |  |  |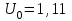
4РАСЧЕТ СТАТИЧЕСКОЙ УСТОЙЧИВОСТИ СИСТЕМЫ
4.1 Устойчивость простейшей электрической системы
иидеальный предел мощности
При ориентировочных расчетах (п. 1.1–1.3задания) предполагается, что устройства АРВ безынерционны и обеспечивают отсутствие самораскачивания. Предел передаваемой мощности определяется по максимуму статической угловой характеристики мощности
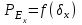. Действие регуляторов возбуждения отражается введением соответствующих эдс 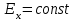, приложенных за индуктивным сопротивлением 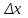. Устойчивая часть угловой характеристики мощности определяется прямым критерием статической устойчивости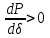
[1-3].Коэффициент запаса статической устойчивости по мощности
(
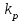)определяется как 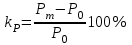. (4.1)При определении запаса статической устойчивости нерегулируемой системы без учета явнополюсностигенератор представляется в схеме замещения синхронным индуктивным сопротивлением по продольной оси
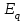и приложенной за ним синхронной эдс Угловая характеристика мощности имеет вид 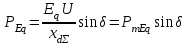, (4.2) где
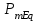–идеальный предел мощности нерегулируемой передачи, 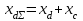.Идеальный предел передаваемой мощности при наличии АРВ пропорционального действия определяется приближенно [2] без учета явнополюсности для обоих типов генераторов пр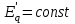и
и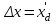 : 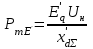. (4.3)При АРВ сильного действия (
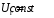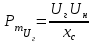, ) . (4.4)По результатам проведенных расчетов необходимо сделать выводы о влиянии различных факторов на запас статической устойчивости. Величина запаса статической устойчивости в нормальном режиме должна быть не меньше 20%.
Пример 3–Расчет запаса статической устойчивости
-
Без АРВ–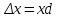
; расчет без учета явнополюсности:
==1,88 + 0,26 = 2,14
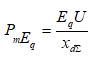
= 2,24*1/2,14 = 1,047
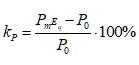
= (1,047-0,64)/0,64*100 = 63,59%
-
Расчет с АРВ пропорционального действия:
;
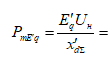
= 1,183*1/(0,26+0,27) = 2,232
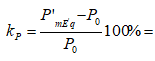
= (2,232-0,64)/0,64*100 = 249%
-
При наличии АРВ сильного действия
;
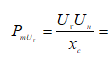
= (1,11*1)/0,26 =4,27
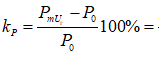
= (4,26-0,64)/0,64*100 = 566%
Результаты расчетов сведены в таблицу 4.1
Таблица 4.1
Результаты расчетов коэффициентазапаса статической устойчивости по мощности
| Вид регулирования | Pm | kp % |
| Генератор без АРВ (без учета явнополюсности) | 1,047 | 63,59 % |
| Генератор с АРВ ПД | 2,232 | 249 % |
| Генератор с АРВ СД | 4,27 | 566 % |
5.РАСЧЕТ ДИНАМИЧЕСКОЙ УСТОЙЧИВОСТИ СИСТЕМЫ
5.1 Общие положения
Анализ динамической устойчивости основан на решении дифференциального уравнения относительного движения ротора и применении правила площадей. При упрощенных расчетах динамической устойчивости делаются следующие основные допущения [1, 2]:
– активная мощность первичного двигателя (турбины) остается неизменной
В течение всего переходного процесса;
– электрическая мощность, вырабатываемая генератором, изменяется мгно-
венно при изменении схемы передачи вследствие КЗ или коммутации;
– не учитываются апериодические моменты, обусловленные потерями
мощности.
Дифференциальное уравнение относительного движения ротора с учетом допущений для простейшей схемы передачи может быть записано в виде [1, 2]
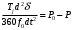
, (5.1)
где
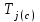–постоянная инерции; t(c) – время;f0 – 50 Гц; (эл. градус); 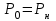– мощность турбины (нагрузки).Электрическая мощность генератора
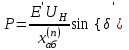без учета явнополюсности определяется по динамической угловой характеристике мощности . (5.2) Здесь 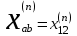– взаимное сопротивление между точкой приложения эдс 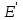и шинами системы с 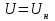для состояния (n) схемы.В дальнейшем принимаем 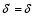. Вторая производная углового пути по времени 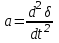является ускорением.Текущее состояние (n) схемы включает нормальное, аварийное состояние,
определяемое видом аварии, и послеаварийное.
Критерием динамической устойчивости синхронных машин является правило (способ) площадей.м Устойчивость сохраняется в случае, если энергия возможного торможения больше энергии ускорения. Геометрическим аналогом энергии являются соответствующие площадки, построенные на основе угловых характеристик мощности (рис. 5.1) при этом
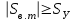. Рис. 5.1 – Применение правила площадей
На рис. 5.1
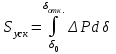
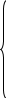; – площадка ускорения; 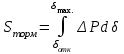–площадка торможения (5.3) 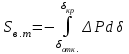–площадка возможного торможения,где
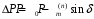.При трехфазном коротком замыкании на сквозной передаче электромагнитная мощность падает до нуля (Рис.5.2).
Рис.5.2 –Угловые характеристики мощности при трехфазном КЗ
При этом должны быть равны между собой площадки, соответствующие избыточным кинетическим энергиям ускорения и торможенияДля критического случая предельный угол отключениятрехфазного КЗ[1]
при
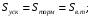В выражении (5.4) углы выражаются в радианах (1радиан 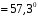). .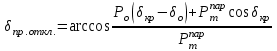 (5.4)Здесь:
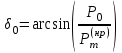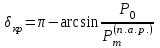
, начальный и критический, с точки зрения сохранения устойчивости угол.
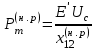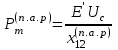
, амплитуды угловых характеристик мощности исходного (нормального) и послеаварийного режимов соответственно.
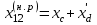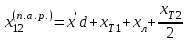
, взаимные сопротивления нормального и послеаварийного режимов соответственно.
Трехфазное КЗ в точкахК1, К2 и К4 эквивалентно разрыву передачи, и на время КЗ можно получить аналитическое решение дифференциального уравнения 5.1 дающее выражение для закона изменения угла
во времени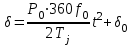 . (5.5)Возрастание угла происходит по квадратичной параболе, а предельное
время, отвечающее предельному значению угла
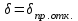или tпр.отк, находится из уравнения 5.5 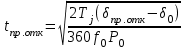с. (5.6)В выражениях (5.5)-(5.6) углы выражаются в градусах, а постоянная времени
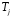и время 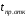в секундах, 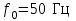.Анализ динамической устойчивости методом площадей в СРС используется для вычисления коэффициента запаса динамической устойчивости, определения предельного угла отключения короткого замыкания и определения предельной передаваемой мощности при отключении одной цепи двухцепной линии электропередачи.