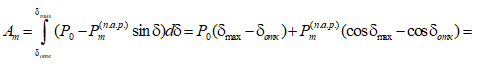Для применения метода площадей необходимо построить угловые характеристики мощности нормального, аварийного и послеаварийного режимов. Характер относительного движения ротора при определении предельной передаваемой мощности при отключении одной цепи двухцепной линии будет рассмотрен в разделе 5.2.

Запас динамической устойчивости оценивается по модулю отношения площади площадки возможного торможения к площадке фактического ускорения. Так, для рис. 5.2

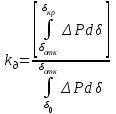, (5.7)

При этом

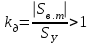
В случае нарушения динамической устойчивости

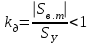
Для определения предельного угол отключения КЗ– 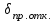и предельного времени отключения КЗ используются формулы (5.4) и (5.6).

Пример 4–Расчет угловых характеристик мощности

Нормальный (исходный) режим:


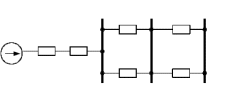
Рис. 5.3 – Схема замещения исходного режима

E^/ = 1,183;



= 0,26+0,27 = 0,53



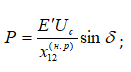
₌ 2,232

Аварийный режим – короткое замыкание в точке К2 вид КЗ– трехфазное. Взаимное сопротивление при трехфазном КЗ на сквозной передаче 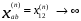. Электрическая мощность генератора =0.

Послеаварийный режим (отключение одной цепи).



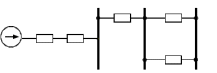
Рис. 5.4– Схема замещения послеаварийного режима



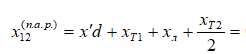
= 0,53 + 0,103 + 0,117 + 0,197/2 = 0,85

;

---

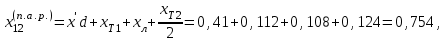
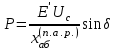= 1,39

Данные для построения угловых характеристик приведены в табл. 5.1.

Таблица 5.1

---

Результаты расчетов угловых характеристик мощности

δ	0	10	20	30	40	50	60	70	80	90
Р(н.р)	0	0,387596	0,763414	1,116037	1,434749	1,709868	1,933033	2,097464	2,198165	2,232075
Р(3)	0	0	0	0	0	0	0	0	0	0
Р(n.a.p)	0	0,241677	0,476011	0,695882	0,894608	1,066153	1,205303	1,307831	1,37062	1,391765
P0	0,64	0,64	0,64	0,64	0,64	0,64	0,64	0,64	0,64	0,64

По данным табл. 5.1 строятся угловые характеристики мощности режимов. Отметим, что при КЗ в точке К1 послеаварийный режим совпадает с нормальным.

---

Пример 5–Расчет динамической устойчивости системы

при трехфазном КЗ
Исходные данные: Частота 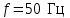, Р₀ = 0,64, Т _J(C) = 4с

Амплитуды угловых характеристик мощности исходного (нормального) и послеаварийного режимов соответственно:

Рm(н.р.) = 2,232, Рm(n.a.p) = 1,39



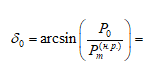
= arcsin(0,64/2,232) =16,67⁰

начальный угол,



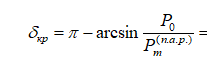
= 180 -16,67 = 163,33⁰ = 2,85 рад – критический угол

Угол выбега ротора генератора в градусах (угол отключения КЗ) при длительности трехфазного КЗ t = 0,4c


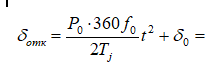
_{= (0,64*360*50)/(2*4)*0,4^2 +16,67 = 67,07⁰ = 1,17 рад}

Предельный угол отключения КЗ в радианах, необходимый для сохранения устойчивости.



= arccos((0,64*(2,85-0,29)+1,39cos(2,85))/1,39) =1,35=77,24⁰
Предельное время отключения КЗ



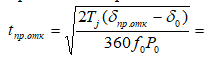
= (2*4*(77,24-16,67)/(360*50*0,64))^0,5 = 0,205 c
При 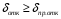динамическая устойчивость не сохраняется и время КЗ

не может быть больше .

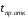Работа (энергия) ускорения пропорциональная площади площадки ускорения



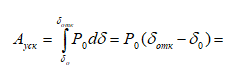
= 0,64 *(77,24-16,67) = 0,677

Максимальный угол выбега ротора 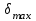может быть найден итерационным методом, например методом простой итерации (методом последовательных приближений)из условия равенства площадок ускорения и торможения решением интегрального уравнения: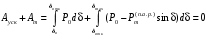



Решение уравнения подготовленное к использованию метода простой итерации имеет вид:

---

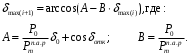
В настоящем примере



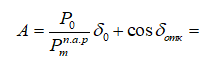
=0,64/1,39*0,29+cos(1,17) = 0,5237

B= 0,64/1,39 = 0,46

δmax(1) = δотк = 1,17

Таблица 5.2

Расчет максимального угла выбега ротора

δmax(i+1)	δmax(i)
1,17	1,585297
1,585297	1,777808
1,777808	1,869301
1,869301	1,913653
1,913653	1,935401
1,935401	1,946132
1,946132	1,951443
1,951443	1,954075
1,954075	1,955382
1,955382	1,95603
1,95603	1,956352
1,956352	1,956511
1,956511	1,956591
1,956591	1,95663
1,95663	1,95665
1,95665	1,956659
1,956659	1,956664

<sub>Окончательно:

δmax = 1,956 рад

Все углы в расчетных формулах в радианах. Процесс может сходиться достаточно медленно и потребовать до 10 итераций. По полученным результатам на угловые характеристики мощности (Рис 5.5) наносятся площадки ускорения и торможения.

Площадь площадки торможения при этом должна равняться по модулю площади площадки ускорения</sub>

---

Смотрите также файлы

• Коби Бин Брайант Детство Брайант родился в Филадельфии 2 августа 1978 года.pptx

• Инв. подл. Подп и дата.docx

• Статья 13, п. 3 Федерального закона 273фз Об образовании в Российской Федерации.docx

• 1 подчиняться командиру звена гдзс, знать поставленную боевую задачу своего звена гдзс и выполнять ее 2.docx

• Программа среднего профессионального образования 44. 02. 02 Преподавание в начальных классах Дисциплина Безопасность жизнедеятельности Практическое занятие 2 (Для юношей).docx