Файл: Для заданной схемы электропередачи определить запас статической.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 27.10.2023
Просмотров: 129
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
,  (рис. 6.2).
(рис. 6.2).
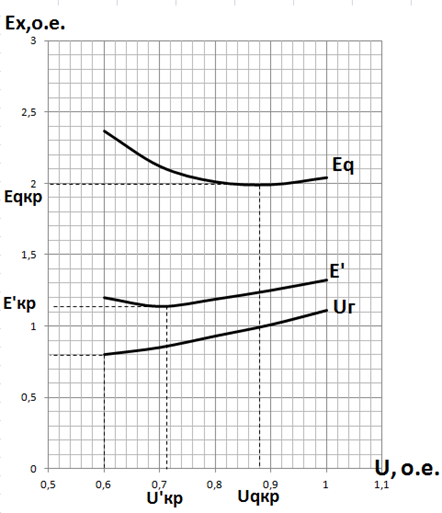
Рис. 6.2 – Зависимость эдс от вида регулирования
Коэффициенты запаса статической устойчивости по напряжению определяются по выражению (6.3) и приведены в таблице 6.2.
Критические напряжения и коэффициенты запаса статической устойчивости по напряжению представлены в табл. 6.3.
Таблица 6.2
Результаты расчетов эдс ( )в зависимости от вида регулирования
)в зависимости от вида регулирования
Таблица 6.3
Результаты расчетов коэффициентов запаса устойчивости типовой нагрузки
Анализ расчета, показывает, что статическая устойчивость сохраняется как при отсутствии АРВ, так и при всех видах регулирования, однако при отсутствии АРВ коэффициент запаса недостаточный. Чем сильнее регулирование возбуждения, тем больше коэффициент запаса статической устойчивости по напряжению и тем статически устойчивее нагрузка (больший коэффициент запаса).
7. РАСЧЕТ ДИНАМИЧЕСКОЙ УСТОЙЧИВОСТИ
АСИНХРОННОЙ НАГРУЗКИ
Критерием динамической устойчивости асинхронных двигателей является преобладание электромагнитного вращающего момента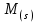 над механическим моментом сопротивления
над механическим моментом сопротивления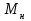 [1-3].
[1-3].
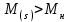 (7.1)
(7.1)
Предельное время АВР или время выбега при отключении(допустимое время перерыва электроснабжения)может быть найдено как время, за которое электродвигатель от начального скольжения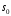 доходит под воздействием либо только механического момента (рис.7.1а), либо разности механического и остаточного электромагнитного до скольжения
доходит под воздействием либо только механического момента (рис.7.1а), либо разности механического и остаточного электромагнитного до скольжения
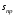 (рис.7.1б).
(рис.7.1б).
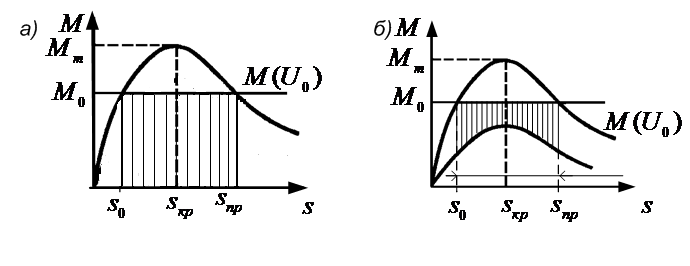 Рис. 7.1– Характеристики моментов
Рис. 7.1– Характеристики моментов
Расчет динамической устойчивости производится упрощенно и без учета электромагнитных переходных процессов в обмотках двигателя[1,4]. Изменение скольжения при изменении режима находится в общем случае численным интегрированием нелинейного уравнения движения асинхронного двигателя:
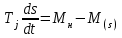 . (7.2)
. (7.2)
Здесь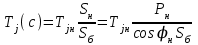 –постоянная инерции движения, приведен-
–постоянная инерции движения, приведен-
ная к базисной мощности, с;
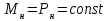 (для рассматриваемого случая) номинальныймеханичский
(для рассматриваемого случая) номинальныймеханичский
момент сопротивленияо.е.;
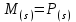 –электромагнитный момент двигателяо.е., определяемый
–электромагнитный момент двигателяо.е., определяемый
выражением
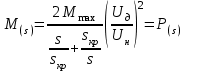 ,(7.3)
,(7.3)
где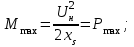
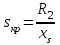 .
.
В выражениях (7.2), (7.3) все величины, кроме постоянной инерции, определяются в относительных единицах при базисных условиях.
Для наиболее тяжелого случая – постоянства механического момента и отсутствия остаточного электромагнитного (рис. 7.1а) задача определения предельного времени АВР АД может быть решена аналитическипри начальных условиях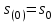 .
.
Для определения предельного времени перерыва электроснабжения (допускаемое время из условий успешного самозапуска) необходимо определить время достижения предельного скольжения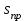 , которое при
, которое при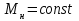 определяется при
определяется при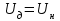 и
и 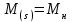 , то есть
, то есть
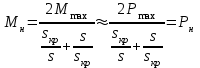 ,(7.4)
,(7.4)
Корни уравнения (7.4) дают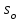 и
и 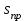 .
.
Решение дифференциального уравнения (7.2) при этом упрощается (так как М
(s)=0) и сводится к виду
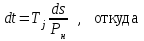
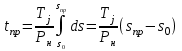 . (7.5)
. (7.5)
Пример 8 – Определение допустимого времени перерыва
электроснабжения по условиям самозапуска
Для оценки возможности самозапуска [7] при заданном времени и месте трехфазного КЗ необходимо определить изменение скольжения за заданное время перерыва электроснабжения.
Приведенная к базисным условиям электромеханическая постоянная времени эквивалентного асинхронного электродвигателя:
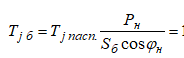
= 10*150/(235*0,87) = 7,34 с
Активное сопротивление схемы замещения эквивалентного асинхронного двигателя определяется как составляющая полного сопротивления в номинальном режиме:
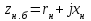 ;
; 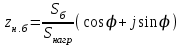 ;
;
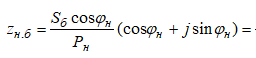
= 235*0,87/150 *(0.87 + j*0,49) = 1,186+J 0,668
Xн = Xs = 0,668, Rн = r2 = 1,186, S0 = 0,018, R2 = r2*S0 = 1,186*0,018 =
= 0,0213
Уравнение (7.4) приводим к виду квадратного уравнения и находим его корни:
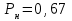 ,
, 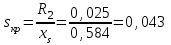 ,
, 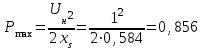 ,
,
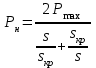 ,
, 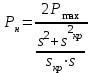 ,
, 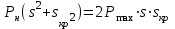 ,
,
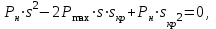
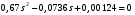 ,
,
Решение дает два значения, одно из которых
– исходное значение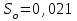 , второе–
, второе–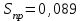 .
.
Предельное время перерыва электроснабжения
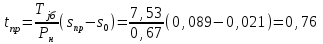 (с).
(с).
При заданном времени перерыва электроснабжения (времени АВР–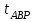 ) должно выполняться условие
) должно выполняться условие
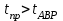 .
.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
пособие/ Ю.А. Куликов.- Новосибирск: Изд-во НГТУ; М:Мир:АСТ, 2003.-
Омск: Изд-во ОмГТУ, 2006. 48 с.
ПриложениеА
 (рис. 6.2).
(рис. 6.2).
Рис. 6.2 – Зависимость эдс от вида регулирования
Коэффициенты запаса статической устойчивости по напряжению определяются по выражению (6.3) и приведены в таблице 6.2.
Критические напряжения и коэффициенты запаса статической устойчивости по напряжению представлены в табл. 6.3.
Таблица 6.2
Результаты расчетов эдс (
 )в зависимости от вида регулирования
)в зависимости от вида регулирования| U | 1,0 | 0,9 | 0,8 | 0,7 | 0,6 |
| P | 1,00 | 0,94 | 0,89 | 0,86 | 0,83 |
| Q | 1,00 | 0,89 | 0,84 | 0,88 | 0,98 |
| P* | 0,67 | 0,63 | 0,60 | 0,57 | 0,56 |
| Q* | 0,33 | 0,29 | 0,28 | 0,29 | 0,32 |
| Eq | 2,04 | 1,99 | 2,01 | 2,12 | 2,37 |
 | 1,32 | 1,25 | 1,2 | 1,14 | 1,2 |
| Uг | 1,11 | 1,01 | 0,93 | 0,85 | 0,8 |
Таблица 6.3
Результаты расчетов коэффициентов запаса устойчивости типовой нагрузки
| Вид регулирования | 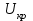 | 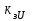 % % |
| Генератор без АРВ (без учета явнополюсности) | 0,88 | 12 % |
| Генератор с АРВ ПД | 0,72 | 28 % |
| Генератор с АРВ СД |  0,6 0,6 |  40 % 40 % |
Анализ расчета, показывает, что статическая устойчивость сохраняется как при отсутствии АРВ, так и при всех видах регулирования, однако при отсутствии АРВ коэффициент запаса недостаточный. Чем сильнее регулирование возбуждения, тем больше коэффициент запаса статической устойчивости по напряжению и тем статически устойчивее нагрузка (больший коэффициент запаса).
7. РАСЧЕТ ДИНАМИЧЕСКОЙ УСТОЙЧИВОСТИ
АСИНХРОННОЙ НАГРУЗКИ
Критерием динамической устойчивости асинхронных двигателей является преобладание электромагнитного вращающего момента
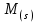 над механическим моментом сопротивления
над механическим моментом сопротивления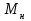 [1-3].
[1-3].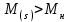 (7.1)
(7.1)Предельное время АВР или время выбега при отключении(допустимое время перерыва электроснабжения)может быть найдено как время, за которое электродвигатель от начального скольжения
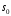 доходит под воздействием либо только механического момента (рис.7.1а), либо разности механического и остаточного электромагнитного до скольжения
доходит под воздействием либо только механического момента (рис.7.1а), либо разности механического и остаточного электромагнитного до скольжения
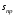 (рис.7.1б).
(рис.7.1б). Рис. 7.1– Характеристики моментов
Рис. 7.1– Характеристики моментов Расчет динамической устойчивости производится упрощенно и без учета электромагнитных переходных процессов в обмотках двигателя[1,4]. Изменение скольжения при изменении режима находится в общем случае численным интегрированием нелинейного уравнения движения асинхронного двигателя:
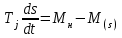 . (7.2)
. (7.2)Здесь
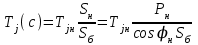 –постоянная инерции движения, приведен-
–постоянная инерции движения, приведен-ная к базисной мощности, с;
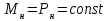 (для рассматриваемого случая) номинальныймеханичский
(для рассматриваемого случая) номинальныймеханичскиймомент сопротивленияо.е.;
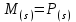 –электромагнитный момент двигателяо.е., определяемый
–электромагнитный момент двигателяо.е., определяемыйвыражением
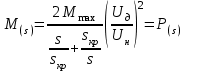 ,(7.3)
,(7.3)где
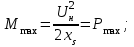
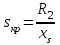 .
.В выражениях (7.2), (7.3) все величины, кроме постоянной инерции, определяются в относительных единицах при базисных условиях.
Для наиболее тяжелого случая – постоянства механического момента и отсутствия остаточного электромагнитного (рис. 7.1а) задача определения предельного времени АВР АД может быть решена аналитическипри начальных условиях
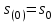 .
.Для определения предельного времени перерыва электроснабжения (допускаемое время из условий успешного самозапуска) необходимо определить время достижения предельного скольжения
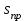 , которое при
, которое при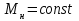 определяется при
определяется при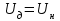 и
и 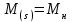 , то есть
, то есть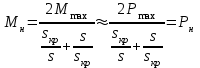 ,(7.4)
,(7.4)Корни уравнения (7.4) дают
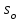 и
и 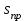 .
.Решение дифференциального уравнения (7.2) при этом упрощается (так как М
(s)=0) и сводится к виду
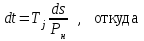
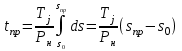 . (7.5)
. (7.5)Пример 8 – Определение допустимого времени перерыва
электроснабжения по условиям самозапуска
Для оценки возможности самозапуска [7] при заданном времени и месте трехфазного КЗ необходимо определить изменение скольжения за заданное время перерыва электроснабжения.
Приведенная к базисным условиям электромеханическая постоянная времени эквивалентного асинхронного электродвигателя:
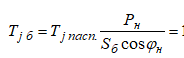
= 10*150/(235*0,87) = 7,34 с
Активное сопротивление схемы замещения эквивалентного асинхронного двигателя определяется как составляющая полного сопротивления в номинальном режиме:
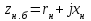 ;
; 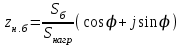 ;
;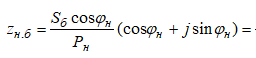
= 235*0,87/150 *(0.87 + j*0,49) = 1,186+J 0,668
Xн = Xs = 0,668, Rн = r2 = 1,186, S0 = 0,018, R2 = r2*S0 = 1,186*0,018 =
= 0,0213
Уравнение (7.4) приводим к виду квадратного уравнения и находим его корни:
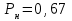 ,
, 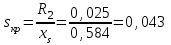 ,
, 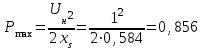 ,
,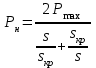 ,
, 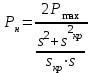 ,
, 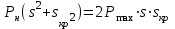 ,
,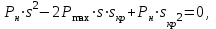
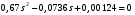 ,
,Решение дает два значения, одно из которых
– исходное значение
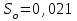 , второе–
, второе–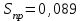 .
.Предельное время перерыва электроснабжения
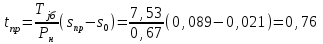 (с).
(с).При заданном времени перерыва электроснабжения (времени АВР–
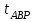 ) должно выполняться условие
) должно выполняться условие
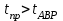 .
.БИБЛИОГРАФИЧЕСКИЙ СПИСОК
-
Эрнст А.Д.Электромеханические переходные процессы в электрических системах: Курс лекций/ А.Д. Эрнст, - Нижневартовск: Изд-во НВГУ, 2013. 130 с.: ил. -
Веников В.А. Переходные электромеханические процессы в электрических системах/ В.А. Веников. - М.: Высш.шк., 1985. -416 с.: ил. -
Куликов Ю.А. Переходные процессы в электрических системах: учеб.
пособие/ Ю.А. Куликов.- Новосибирск: Изд-во НГТУ; М:Мир:АСТ, 2003.-
-
с.: ил.
-
Эрнст А.Д.Электромагнитные переходные процессы в электроэнергетических системах : Курс лекций / А.Д. Эрнст. - Нижневартовск: Изд-во НГГУ, 2012. 199 с.: ил. -
Переходные процессы в электроэнергетических системах. : учебник для вузов/И.П. Крючков, В.А. Старшинов, Ю.П. Гусев, М.В Пиаторов; под ред. И.П. Крючкова. М.:Издательский дом МИ 2008-416с.:ил. -
Эрнст А.Д. Расчет токов короткого замыкания в электрических системах : Учеб. пособие / А.Д. Эрнст.-Нижневартовск: Изд-во НГГУ, 2012. 86с.: и -
Эрнст А.Д.Самозапуск асинхронных электродвигателей: Учеб. пособие/ А.Д. Эрнст.-Омск: Изд-во ОмГТУ,2006. 48 с.: ил.
Омск: Изд-во ОмГТУ, 2006. 48 с.
ПриложениеА