Файл: Лекции по теоретической метрологии.doc

В метрологической литературе, как правило, описываются не только методы выявления и исключения систематических погрешностей, но и методы обнаружения грубых погрешностей и отбраковывания результатов с такими погрешностями. Отдельно рассматривают применение аппарата теории вероятностей и математической статистики для получения вероятностной оценки случайных погрешностей. В итоге представление о поиске и оценке погрешностей, составленное на базе нескольких источников, может получиться довольно противоречивым из-за несовпадения терминологии и отсутствия обобщенного подхода. Многочисленные частные методы выявления, оценки и исключения систематических погрешностей окончательно запутывают картину.

Методы выявления и оценки погрешностей в ряде случаев могут распространяться не только на систематические, но и на случайные погрешности, о чем обычно не говорят, поскольку случайные погрешности индивидуально непредсказуемы. Следует иметь в виду, что в полученных конкретных результатах измерений погрешности и их составляющие имеют фиксированные значения и поддаются экспериментальной оценке.

Поскольку для любых физических величин, как правило, может быть разработана методика выполнения измерений более точная, чем применяемая, следует признать, что при наличии методов оценки погрешности измерений появляется принципиальная возможность выявления и количественной оценки «a posteriori» не только систематических, но и случайных погрешностей измерений. Это нисколько не противоречит определению случайной погрешности как случайной величины в части невозможности предсказания ее конкретного значения.

Результаты многократных измерений одной и той же физической величины или закономерно изменяющихся величин могут быть объектом анализа для выявления систематической составляющей и оценки случайных составляющих погрешностей измерений. Анализ базируется на оценке тенденции изменения результатов измерений. Сравнение полученной тенденции с идеальной дает возможность судить о наличии систематической погрешности и характере ее изменения. Например, возрастающие (убывающие) результаты при повторных измерениях одной и той же величины свидетельствуют о наличии прогрессирующей систематической составляющей погрешности измерений.

Систематические погрешности могут иметь место и при измерении разных или изменяющихся физических величин. Линейное или другое закономерное изменение градуировочной характеристики прибора с равномерной шкалой позволяет выявить прогрессирующую или периодическую составляющую погрешности прибора, либо систематическую погрешность прибора, описываемую более сложными функциями.

---

Более полные количественные оценки погрешностей можно получить только при наличии заведомо более точной информации об измеряемой физической величине.

Анализ характерных особенностей методов выявления и оценки погрешностей позволяет сделать вывод о наличии общих подходов к выявлению и оценке значений погрешностей вне зависимости от характера их изменения. Общие методы выявления и оценки погрешностей равным образом распространяются на систематические, случайные и грубые погрешности и в принципе позволяют выявлять любые погрешности измерений независимо от их характера.

---

МОДУЛЬ 7. АНАЛИЗ ТОЧЕЧНЫХ ДИАГРАММ

Анализ точечных диаграмм результатов многократных измерений одной и той же физической величины (серии измерений) является сравнительно простым и достаточно эффективным средством выявления и оценки погрешностей. Он позволяет выявлять и оценивать переменные систематические и случайные составляющие погрешности измерений и отбраковывать результаты с явно выраженными грубыми погрешностями.

Точечную диаграмму строят в координатах «результат измерения (наблюдение при измерении) X – номер измерения n». При построении диаграммы из технических соображений по оси ординат обычно предпочитают откладывать не сами результаты измерений, а их отклонения от некоторого условного значения. Масштаб желательно выбрать таким, чтобы размах R результатов измерений на диаграмме можно было оценить двумя значащими цифрами.

И деальная точечная диаграмма серии измерений должна представлять собой ряд точек, располагающихся на одинаковой высоте, которая соответствует истинному значению измеряемой физической величины Q (рисунок 7.1).

Постоянная систематическая погрешность вызывает только эквидистантное смещение экспериментальной тенденции относительно идеальной, а характер тенденции при этом не меняется. Поэтому делать какие-либо выводы о постоянной составляющей погрешности в серии измерений по точечной диаграмме нельзя. Можно только высказать предположение о наличии такой погрешности на основании постулата об обязательном присутствии в погрешности измерения систематической составляющей, которая в лучшем случае будет пренебрежимо мала по сравнению со случайной составляющей.

Тенденция изменения результатов измерений в серии может быть вызвана только наличием систематической переменной погрешности определенного вида, следовательно, при наличии точечной диаграммы появляется возможность качественного описания такой погрешности, которое может быть дополнено некоторыми количественными (числовыми) оценками. Наличие значимых случайных составляющих погрешности в каждом из наблюдений затрудняет анализ диаграммы, однако достаточно продолжительные серии, как правило, позволяют выявить тенденции, если они имеют место.

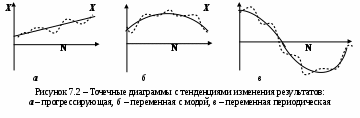
Тенденции изменения результатов в сериях измерений, проявляющиеся на точечных диаграммах, представлены на рисунке 7.2 (7.2

---

а – наклон, 7.2б – мода, 7.2в – гармонические изменения аппроксимирующей линии).

Наличие закономерностей изменения результатов свидетельствуют о присутствии в серии переменных систематических погрешностей. Характер таких погрешностей в первом приближении можно оценить по виду наблюдаемой тенденции изменения результатов (монотонно возрастающие или убывающие, переменные с одним или несколькими экстремумами…), для оформления которой используют аппроксимирующие линии. Аппроксимацию, как правило, осуществляют простейшими линиями: прямой, участком дуги окружности или параболы, для периодических изменений – чаще всего синусоидой (косинусоидой).



Отклонения результатов от аппроксимирующей линии могут рассматриваться как случайные составляющие погрешности измерения. Если отклонения результатов от аппроксимирующей линии полагают случайными, их оценивают предельными (максимальным) значениями – либо одним (максимальным по модулю), либо двумя (максимальными верхним и нижним с учетом знака). Значения отклонений определяют в направлении оси ординат точечной диаграммы с учетом масштаба. Сумма модулей двух максимальных отклонений (верхнего и нижнего) составляет размах случайных отклонений, который чаще всего используют для ориентировочной оценки случайной составляющей погрешности измерения. Более представительной оценкой принято считать среднее квадратическое значение отклонений, которое рассчитывают с использованием статистической обработки всех значений отклонений в серии.

Следует помнить, что точечная диаграмма не является графиком результатов измерений, поскольку по оси абсцисс не откладывают аргумент какой-либо функции. Любая тенденция изменения результатов свидетельствует только об изменении во времени аргументов, вызывающих переменные систематические погрешности измерений, причем сам аргумент по точечной диаграмме выявить невозможно. Проведение аппроксимирующей линии и оценка тенденции и отклонений от нее осуществляются на основе предположения (допущения) о равномерном изменении аргумента от измерения к измерению, что приводит к закономерному изменению результатов. Такое допущение накладывает определенные ограничения на методику проведения серии многократных измерений одной и той же физической величины. Обязательными условиями являются неизменность самой измеряемой физической величины и методики выполнения ее измерений. Наблюдения следует проводить через примерно одинаковые промежутки времени без перерывов для сохранения постоянства условий в широком смысле, включая не только поддержание влияющих величин в нормальной или рабочей области значений, но и психофизиологическое состояние оператора. Серию не следует продолжать до явного утомления оператора, а его замена может привести к фактическому получению второй серии.

---

Многократные измерения одной и той же физической величины с использованием одной методики выполнения измерений позволяют численно оценить сходимость измерений внутри серии. Высокая сходимость результатов отражается на диаграмме отсутствием тенденций изменения результатов и малыми случайными отклонениями от аппроксимирующей линии.

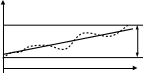
В качестве первичной оценки погрешности измерений в серии, включающей систематическую и случайную составляющие, может быть использован размах результатов многократных измерений (рисунок 7.3)

R′ = X_max – X_min.

Чтобы получить геометрическое представление размаха R′ результатов измерений в серии, следует провести две прямые, параллельные оси абсцисс, через самую верхнюю и самую нижнюю точки точечной диаграмме.

Размах R' включает в себя как рассеяние результатов из-за случайной составляющей погрешности измерений, так и переменную систематическую составляющую погрешности (при ее наличии), вызывающую закономерное изменение результатов во времени. Для того чтобы можно было отдельно рассматривать влияние на измерения детерминированных и стохастических воздействий, из результатов измерений исключают систематические составляющие погрешностей. Такую операцию называют «исправлением результатов измерений», а результаты измерений после исключения из них систематических погрешностей считают «исправленными». В соответствии со сказанным, следует различать размахи «неисправленных» R' и «исправленных» R результатов измерений.


Х Х

R' R'

NN

а б
Рисунок 7.3 – Размахи R' результатов на точечных диаграммах без тенденции изменения результатов а и с прогрессирующей тенденцией б


Полное исправление результатов требует абсолютной строгости в определении систематических составляющих погрешностей каждого из результатов измерений, что невозможно осуществить с помощью точечной диаграммы. Даже если принятые при ее построении допущения соответствуют реальной ситуации, постоянная составляющая систематических погрешностей всегда остается невыявленной. Однако с использованием точечной диаграммы можно осуществить «частичное исправление» результатов измерений. Для этого на экспериментальные точки накладывают аппроксимирующую линию, которая отражает изменения результатов из-за систематических погрешностей. Если считать, что

---