ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 360
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
МОДУЛЬ 1. Предметная область метрологии
МОДУЛЬ 2. ШКАЛЫ И ПРИМЕНЕНИЕ ИХ В МЕТРОЛОГИИ
МОДУЛЬ 3. Физические величины, системы единиц физических величин
МОДУЛЬ 4. КЛАССИФИКАЦИЯ ИЗМЕРЕНИЙ. ПОНЯТИЕ О КАЧЕСТВЕ ИЗМЕРЕНИЙ
МОДУЛЬ 5. КЛАССИФИКАЦИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЙ
МОДУЛЬ 6. МЕТОДЫ ВЫЯВЛЕНИЯ И ИСКЛЮЧЕНИЯ ПОГРЕШНОСТЕЙ
МОДУЛЬ 7. АНАЛИЗ ТОЧЕЧНЫХ ДИАГРАММ
МОДУЛЬ 8. МАТЕМАТИЧЕСКАЯ ОБРАБОТКА И ФОРМЫ ПРЕДСТАВЛЕНИЯ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
МОДУЛЬ 13. СРЕДСТВА ИЗМЕРЕНИЙ. МЕТРОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ СРЕДСТВ ИЗМЕРЕНИЙ
МОДУЛЬ 14. ЭТАЛОНЫ ЕДИНИЦ ФИЗИЧЕСКИХ ВЕЛИЧИН И ПЕРЕДАЧА ЕДИНИЦ ОТ ЭТАЛОНОВ
отклонения результатов от построенной тенденции их изменения вызваны собственно случайными составляющими погрешности, можно перейти к их количественной оценке.
В этом случае делается допущение, что аппроксимирующая линия полностью отражает систематические изменения результатов (линия «текущего среднего значения»), а отклонения от этой линии рассматривают как случайные составляющие погрешности каждого из наблюдений. Числовые оценки отклонений определяют по точечной диаграмме с учетом ее масштаба. Предложенный прием позволяет разделить и наглядно представить на диаграмме систематические и случайные составляющие погрешности измерений.
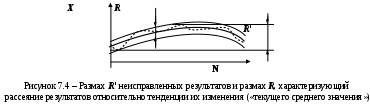
Для оценки размаха R «исправленных» результатов измерений, который отражает рассеяние результатов из-за наличия только случайной составляющей погрешности, с помощью диаграммы исключают влияние переменной систематической составляющей погрешности. Размах R (рисунок 7.4) определяют как расстояние между двумя линиями, проведенными эквидистантно аппроксимирующей линии через две наиболее удаленные от нее точки, а его значение рассчитывают с учетом масштаба точечной диаграммы.
Описанное «исправление» результатов измерений названо частичным, поскольку неизвестное (и потому отсутствующее на диаграмме) истинное значение измеряемой величины искусственно заменяется некоторым «текущим средним значением». «Текущее среднее значение» воспроизводится на диаграмме аппроксимирующей линией, учитывающей влияние переменной части систематической погрешности.
Точечная диаграмма результатов многократных измерений физической величины, полученных с помощью одной методики выполнения измерений, не дает представления о значении постоянной систематической погрешности. Диаграмма одной серии не содержит достаточной информации для такого анализа из-за отсутствия «опорного значения», которым можно было бы заменить истинное.
Анализ результатов измерений каждой отдельной серии обычно начинают с выявления тенденции изменения результатов измерений и ее качественной оценки. Затем на диаграмму наносят аппроксимирующую линию, соответствующую характеру изменения результатов серии. При анализе диаграмм могут встретиться три варианта:
Первый вариант свидетельствует об отсутствии в серии переменной систематической погрешности, диаграмму аппроксимируют прямой линией, параллельной оси абсцисс. Такая аппроксимация свидетельствует о наличии в серии постоянной систематической составляющей погрешности, значение которой оценить невозможно (это может быть значимая либо пренебрежимо малая погрешность).
При отсутствии в серии явно выраженной тенденции изменения результатов ее также как и в первом варианте аппроксимируют прямой линией, параллельной оси абсцисс.
Для аппроксимации диаграмм третьего варианта по возможности выбирают наклонные прямые линии (линейно прогрессирующее в сторону увеличения или уменьшения изменение результатов) или простейшие кривые линии в виде параболы, дуги окружности, синусоиды (прогрессирующее изменение с затуханием, модальное или периодическое изменение результатов). При любой аппроксимации обязательно будут наблюдаться несовпадение результатов и аппроксимирующей линии. Отклонения могут быть вызваны объективными причинами (наличие случайных погрешностей в результатах измерений), или несоответствующей аппроксимацией результатов (неправильный характер и расположение аппроксимирующей линии). Успешность выбора аппроксимирующей зависимости и ее наложения на экспериментальные точки зависит от числа наблюдений и опыта исследователя. Можно проводить аппроксимирующие линии выбранного вида с использованием математических методов (например, метода наименьших квадратов), но точность и достоверность результатов при этом практически не повышается. Поскольку сами погрешности имеют малые значения, а анализ точечных диаграмм основан на допущениях, не обеспечивающих высокий уровень строгости, незначительные погрешности аппроксимации, как правило, имеют второй порядок малости и «погрешности оценки погрешностей» не приводят к существенному искажению результатов исследования.
Чаще всего аппроксимация простейшими линиями оказывается достаточно эффективной, но не исключаются и возможные уточнения, например использование параболы или экспоненты для описания участка прогрессирующих данных или наложение синусоиды на наклонную прямую линию. Однако при этом следует иметь в виду, что стремление к высокой точности в подборе аппроксимирующей линии не имеет смысла, поскольку не гарантирована строгость соответствия точечной диаграммы допущениям, положенным в основу ее построения. Как показывает опыт анализа точечных диаграмм, незначительные различия при моделировании систематических тенденций разными исследователями при оценивании погрешностей приводят к расхождениям второго порядка малости и не оказывают значимого влияния на результаты таких числовых оценок как среднее квадратическое отклонение.
Примерами серий с очевидными тенденциями можно считать точечные диаграммы на рисунке 7.2. На рисунке 7.2а просматривается тенденция увеличения результатов, которую проще всего аппроксимировать прямой линией. Такая тенденция свидетельствует о наличии в результатах прогрессирующей систематической погрешности линейного характера. Тенденция на рисунке 7.2б – немонотонная, результаты сначала увеличиваются, затем после достижения максимума уменьшаются, что позволяет предложить аппроксимацию дугой окружности или участком синусоиды. Немонотонное изменение результатов может свидетельствовать о наличии периодической систематической составляющей, однако для уверенного заключения об этом экспериментальных данных явно недостаточно. Зато на рисунке 7.2в очевидно просматривается периодическая тенденция, которую можно аппроксимировать косинусоидой в 3/4 периода.
После проведения аппроксимирующей линии визуально оценивают экстремальные отклонения от этой линии. При наличии одной или нескольких точек, явно выпадающих из общей тенденции, делается отрицательное заключение об их принадлежности исследуемому массиву результатов измерений. Результаты, соответствующие этим точкам, оценивают как содержащие грубые погрешности и цензурируют, полагая, что они получены ошибочно. Результаты, подозрительные на наличие промахов, но вызывающие сомнения, оставляют для последующего статистического отбраковывания, которое выходит за пределы анализа точечных диаграмм.
Если не наблюдается резко выпадающих из общей тенденции отклонений (результатов с грубыми погрешностями), то через самые удаленные от аппроксимирующей линии точки (максимальные отклонения «в плюс» и «в минус») проводят эквидистанты аппроксимирующей линии. Расстояние между ними вдоль оси ординат в масштабе точечной диаграммы равно размаху отклонений R, и рассматривается как одна из характеристик случайной составляющей погрешности анализируемой серии.
Проведенные на точечной диаграмме аппроксимирующая линия и эквидистанты позволяют количественно оценить не только размахи отклонений R
' (общий размах результатов измерений) и R (размах частично исправленных результатов измерений), но и другие параметры и характеристики точечной диаграммы, включая изменение прогрессирующей составляющей в серии результатов (приращение а в пределах серии), амплитуду А или удвоенную амплитуду 2А периодической составляющей, а также ее ориентировочный период Т в числах (номерах) наблюдений.
Точечная диаграмма в определенных случаях позволяет высказать некоторые суждения не только о сходимости результатов в серии, но и о правильности измерений, поскольку устойчивая тенденция изменения результатов измерений свидетельствует о наличии в них переменной систематической погрешности. Анализ точечных диаграмм позволяет делать логически обоснованные предположения об изменении условий измерений в самом широком понимании этого термина. Например, наличие прогрессирующей тенденции в серии измерений может быть связано с закономерным изменением одной или нескольких влияющих величин, накапливающейся усталостью оператора, накапливающимся воздействием чувствительного элемента на объект измерений. Предположения об износе элементов измерительной цепи средства измерений, как правило, неправомочны, поскольку существенный износ деталей прибора при проведении нескольких десятков или даже сотен измерений может наблюдаться только у особо неудачных конструкций или отдельных экземпляров средств измерений.
Ниже приведены точечные диаграммы (рисунок 7.5), на основании которых проведен анализ результатов измерений каждой из проведенных серий и примеры гипотетических высказываний о возможных причинах характерных особенностей результатов в сериях.
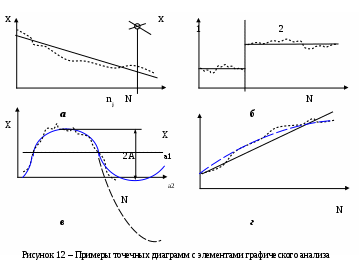
Точечная диаграмма на рисунке 7.5а имеет явно выраженную тенденцию монотонного убывания значений, что свидетельствует о наличии в серии прогрессирующей погрешности (тенденция изменения отражена аппроксимирующей прямой). Результат nj цензурируется как результат с грубой погрешностью – он явно выпадает из общей тенденции, несмотря на то, что его значение близко к значениям в начале серии. Возможные причины появления этого результата – ошибка оператора (промах при манипулировании или при отсчитывании) либо сбой в работе прибора.
Особенностью точечной диаграммы на рисунке 7.5
б является очевидное наличие двух участков 1 и 2, каждый из которых не имеет явно выраженной тенденции изменения результатов. Резкое (скачкообразное) изменение результатов между участками 1 и 2 свидетельствуют о фактическом изменении условий измерений в серии в широком смысле этого термина (возможно, произошло незамеченное изменение влияющей величины, изменилась измеряемая величина, был заменен оператор или случилось некое иное событие), результатом чего стало получение двух серий вместо одной.
Скачкообразное изменение результатов позволяет высказать несколько предположений: возможно, был перерыв в работе, за время которого изменились условия измерений (одна или несколько влияющих величин), могло произойти мгновенное изменение настройки (сбой настройки) прибора. В качестве гипотезы можно также рассмотреть возможную «подмену» измеряемой физической величины, то есть фактический переход от одной из номинально одинаковых физических величин к другой, например, из-за незамеченного изменения контрольного сечения (контрольной точки).
Точечная диаграмма на рисунке 7.5в имеет явно выраженную тенденцию немонотонного изменения значений, что может свидетельствовать о наличии в серии периодической (циклической) погрешности. Возможные тенденции изменения результатов отражены двумя аппроксимирующими линиями – сплошной и штриховой, из которых видно, что предполагаемые тенденции примерно вдвое различаются по периоду и амплитудам. Поскольку для достоверных заключений о наличии периодической погрешности, ее амплитуде и предполагаемом периоде наличной информации недостаточно, по возможности следует продолжить серию измерений, при невозможности – высказать предположения, четко оговаривая принятые допущения.
При выполнении нескольких серий многократных измерений одной и той же физической величины с использованием разных методик выполнения измерений весьма эффективно их сопоставление с помощью точечных диаграмм, построенных в одном масштабе. Анализ каждой из серий измерений включает оценку отдельно по каждой серии тенденций изменения результатов измерений и оценки размахов
В этом случае делается допущение, что аппроксимирующая линия полностью отражает систематические изменения результатов (линия «текущего среднего значения»), а отклонения от этой линии рассматривают как случайные составляющие погрешности каждого из наблюдений. Числовые оценки отклонений определяют по точечной диаграмме с учетом ее масштаба. Предложенный прием позволяет разделить и наглядно представить на диаграмме систематические и случайные составляющие погрешности измерений.
Для оценки размаха R «исправленных» результатов измерений, который отражает рассеяние результатов из-за наличия только случайной составляющей погрешности, с помощью диаграммы исключают влияние переменной систематической составляющей погрешности. Размах R (рисунок 7.4) определяют как расстояние между двумя линиями, проведенными эквидистантно аппроксимирующей линии через две наиболее удаленные от нее точки, а его значение рассчитывают с учетом масштаба точечной диаграммы.
Описанное «исправление» результатов измерений названо частичным, поскольку неизвестное (и потому отсутствующее на диаграмме) истинное значение измеряемой величины искусственно заменяется некоторым «текущим средним значением». «Текущее среднее значение» воспроизводится на диаграмме аппроксимирующей линией, учитывающей влияние переменной части систематической погрешности.
Точечная диаграмма результатов многократных измерений физической величины, полученных с помощью одной методики выполнения измерений, не дает представления о значении постоянной систематической погрешности. Диаграмма одной серии не содержит достаточной информации для такого анализа из-за отсутствия «опорного значения», которым можно было бы заменить истинное.

Анализ результатов измерений каждой отдельной серии обычно начинают с выявления тенденции изменения результатов измерений и ее качественной оценки. Затем на диаграмму наносят аппроксимирующую линию, соответствующую характеру изменения результатов серии. При анализе диаграмм могут встретиться три варианта:
-
серия без тенденции изменения результатов; -
серия без явно выраженной тенденции изменения результатов; -
серия c явной тенденцией изменения результатов.
Первый вариант свидетельствует об отсутствии в серии переменной систематической погрешности, диаграмму аппроксимируют прямой линией, параллельной оси абсцисс. Такая аппроксимация свидетельствует о наличии в серии постоянной систематической составляющей погрешности, значение которой оценить невозможно (это может быть значимая либо пренебрежимо малая погрешность).
При отсутствии в серии явно выраженной тенденции изменения результатов ее также как и в первом варианте аппроксимируют прямой линией, параллельной оси абсцисс.
Для аппроксимации диаграмм третьего варианта по возможности выбирают наклонные прямые линии (линейно прогрессирующее в сторону увеличения или уменьшения изменение результатов) или простейшие кривые линии в виде параболы, дуги окружности, синусоиды (прогрессирующее изменение с затуханием, модальное или периодическое изменение результатов). При любой аппроксимации обязательно будут наблюдаться несовпадение результатов и аппроксимирующей линии. Отклонения могут быть вызваны объективными причинами (наличие случайных погрешностей в результатах измерений), или несоответствующей аппроксимацией результатов (неправильный характер и расположение аппроксимирующей линии). Успешность выбора аппроксимирующей зависимости и ее наложения на экспериментальные точки зависит от числа наблюдений и опыта исследователя. Можно проводить аппроксимирующие линии выбранного вида с использованием математических методов (например, метода наименьших квадратов), но точность и достоверность результатов при этом практически не повышается. Поскольку сами погрешности имеют малые значения, а анализ точечных диаграмм основан на допущениях, не обеспечивающих высокий уровень строгости, незначительные погрешности аппроксимации, как правило, имеют второй порядок малости и «погрешности оценки погрешностей» не приводят к существенному искажению результатов исследования.
Чаще всего аппроксимация простейшими линиями оказывается достаточно эффективной, но не исключаются и возможные уточнения, например использование параболы или экспоненты для описания участка прогрессирующих данных или наложение синусоиды на наклонную прямую линию. Однако при этом следует иметь в виду, что стремление к высокой точности в подборе аппроксимирующей линии не имеет смысла, поскольку не гарантирована строгость соответствия точечной диаграммы допущениям, положенным в основу ее построения. Как показывает опыт анализа точечных диаграмм, незначительные различия при моделировании систематических тенденций разными исследователями при оценивании погрешностей приводят к расхождениям второго порядка малости и не оказывают значимого влияния на результаты таких числовых оценок как среднее квадратическое отклонение.
Примерами серий с очевидными тенденциями можно считать точечные диаграммы на рисунке 7.2. На рисунке 7.2а просматривается тенденция увеличения результатов, которую проще всего аппроксимировать прямой линией. Такая тенденция свидетельствует о наличии в результатах прогрессирующей систематической погрешности линейного характера. Тенденция на рисунке 7.2б – немонотонная, результаты сначала увеличиваются, затем после достижения максимума уменьшаются, что позволяет предложить аппроксимацию дугой окружности или участком синусоиды. Немонотонное изменение результатов может свидетельствовать о наличии периодической систематической составляющей, однако для уверенного заключения об этом экспериментальных данных явно недостаточно. Зато на рисунке 7.2в очевидно просматривается периодическая тенденция, которую можно аппроксимировать косинусоидой в 3/4 периода.
После проведения аппроксимирующей линии визуально оценивают экстремальные отклонения от этой линии. При наличии одной или нескольких точек, явно выпадающих из общей тенденции, делается отрицательное заключение об их принадлежности исследуемому массиву результатов измерений. Результаты, соответствующие этим точкам, оценивают как содержащие грубые погрешности и цензурируют, полагая, что они получены ошибочно. Результаты, подозрительные на наличие промахов, но вызывающие сомнения, оставляют для последующего статистического отбраковывания, которое выходит за пределы анализа точечных диаграмм.
Если не наблюдается резко выпадающих из общей тенденции отклонений (результатов с грубыми погрешностями), то через самые удаленные от аппроксимирующей линии точки (максимальные отклонения «в плюс» и «в минус») проводят эквидистанты аппроксимирующей линии. Расстояние между ними вдоль оси ординат в масштабе точечной диаграммы равно размаху отклонений R, и рассматривается как одна из характеристик случайной составляющей погрешности анализируемой серии.
Проведенные на точечной диаграмме аппроксимирующая линия и эквидистанты позволяют количественно оценить не только размахи отклонений R
' (общий размах результатов измерений) и R (размах частично исправленных результатов измерений), но и другие параметры и характеристики точечной диаграммы, включая изменение прогрессирующей составляющей в серии результатов (приращение а в пределах серии), амплитуду А или удвоенную амплитуду 2А периодической составляющей, а также ее ориентировочный период Т в числах (номерах) наблюдений.
Точечная диаграмма в определенных случаях позволяет высказать некоторые суждения не только о сходимости результатов в серии, но и о правильности измерений, поскольку устойчивая тенденция изменения результатов измерений свидетельствует о наличии в них переменной систематической погрешности. Анализ точечных диаграмм позволяет делать логически обоснованные предположения об изменении условий измерений в самом широком понимании этого термина. Например, наличие прогрессирующей тенденции в серии измерений может быть связано с закономерным изменением одной или нескольких влияющих величин, накапливающейся усталостью оператора, накапливающимся воздействием чувствительного элемента на объект измерений. Предположения об износе элементов измерительной цепи средства измерений, как правило, неправомочны, поскольку существенный износ деталей прибора при проведении нескольких десятков или даже сотен измерений может наблюдаться только у особо неудачных конструкций или отдельных экземпляров средств измерений.
Ниже приведены точечные диаграммы (рисунок 7.5), на основании которых проведен анализ результатов измерений каждой из проведенных серий и примеры гипотетических высказываний о возможных причинах характерных особенностей результатов в сериях.
Точечная диаграмма на рисунке 7.5а имеет явно выраженную тенденцию монотонного убывания значений, что свидетельствует о наличии в серии прогрессирующей погрешности (тенденция изменения отражена аппроксимирующей прямой). Результат nj цензурируется как результат с грубой погрешностью – он явно выпадает из общей тенденции, несмотря на то, что его значение близко к значениям в начале серии. Возможные причины появления этого результата – ошибка оператора (промах при манипулировании или при отсчитывании) либо сбой в работе прибора.
Особенностью точечной диаграммы на рисунке 7.5
б является очевидное наличие двух участков 1 и 2, каждый из которых не имеет явно выраженной тенденции изменения результатов. Резкое (скачкообразное) изменение результатов между участками 1 и 2 свидетельствуют о фактическом изменении условий измерений в серии в широком смысле этого термина (возможно, произошло незамеченное изменение влияющей величины, изменилась измеряемая величина, был заменен оператор или случилось некое иное событие), результатом чего стало получение двух серий вместо одной.
Скачкообразное изменение результатов позволяет высказать несколько предположений: возможно, был перерыв в работе, за время которого изменились условия измерений (одна или несколько влияющих величин), могло произойти мгновенное изменение настройки (сбой настройки) прибора. В качестве гипотезы можно также рассмотреть возможную «подмену» измеряемой физической величины, то есть фактический переход от одной из номинально одинаковых физических величин к другой, например, из-за незамеченного изменения контрольного сечения (контрольной точки).
Точечная диаграмма на рисунке 7.5в имеет явно выраженную тенденцию немонотонного изменения значений, что может свидетельствовать о наличии в серии периодической (циклической) погрешности. Возможные тенденции изменения результатов отражены двумя аппроксимирующими линиями – сплошной и штриховой, из которых видно, что предполагаемые тенденции примерно вдвое различаются по периоду и амплитудам. Поскольку для достоверных заключений о наличии периодической погрешности, ее амплитуде и предполагаемом периоде наличной информации недостаточно, по возможности следует продолжить серию измерений, при невозможности – высказать предположения, четко оговаривая принятые допущения.

При выполнении нескольких серий многократных измерений одной и той же физической величины с использованием разных методик выполнения измерений весьма эффективно их сопоставление с помощью точечных диаграмм, построенных в одном масштабе. Анализ каждой из серий измерений включает оценку отдельно по каждой серии тенденций изменения результатов измерений и оценки размахов