Файл: Лекции по теоретической метрологии.doc

Характеристики погрешности измерений можно указывать в единицах измеряемой величины (абсолютные погрешности) или в относительных единицах (относительные погрешности).

Характеристики погрешностей измерений или статистические оценки:

• 
  среднее квадратическое отклонение погрешности;
  
• 
  среднее квадратическое отклонение случайной погрешности;
  
• 
  среднее квадратическое отклонение систематической погрешности;
  
• 
  нижняя граница интервала погрешности измерений;
  
• 
  верхняя граница интервала погрешности измерений;
  
• 
  нижняя граница интервала систематической погрешности измерений;
  
• 
  верхняя граница интервала систематической погрешности измерений;
  
• 
  вероятность попадания погрешности в указанный интервал.
  

Рекомендуемое значение вероятности Р = 0,95.

Возможные характеристики погрешностей включают аппроксимации функции плотностей распределения вероятностей или статистические описания этих распределений. Функцию плотностей распределения вероятностей погрешности измерений считают соответствующей усеченному нормальному распределению, если есть основания полагать, что реальное распределение симметрично, одномодально, отлично от нуля на конечном интервале значений аргумента, и другая информация о плотности распределения отсутствует.

Если есть основания полагать, что реальное распределение погрешностей отлично от нормального, следует принимать какую-либо другую аппроксимацию функции плотностей распределения вероятностей. В таком случае принятая аппроксимация функции указывается в описании результата измерений, например: «трап.» (при трапециевидном распределении) или «равн.» (при равновероятном).

В состав условий измерений могут входить: диапазон значений измеряемой величины, частотные спектры измеряемой величины или диапазон скоростей ее изменений; диапазоны значений всех величин, существенно влияющих на погрешность измерений, а также, при необходимости, и другие факторы.

Требования к оформлению результата измерений:

• 
  наименьшие разряды должны быть одинаковы у точечной оценки результата и у характеристик погрешностей;
  
• 
  характеристики погрешностей (или их статистические оценки) выражают числом, содержащим не более двух значащих цифр, при этом для статистических оценок цифра второго разряда округляется в большую сторону, если последующая цифра неуказываемого младшего разряда больше нуля;
  
• 
  допускается характеристики погрешностей (или их статистические оценки) выражать числом, содержащим одну значащую цифру, при этом для статистических оценок второй разряд (неуказываемый младший) округляется в большую сторону при отбрасывании цифры младшего разряда равной или больше 5 и в меньшую сторону при цифре меньше 5.
  

---

Примеры представления результатов измерений в различных формах:

1. 
   (8,334 ± 0,012) г; Р = 0,95.
   
2. 
   32,014 мм. Характеристики погрешностей и условия измерений по РД 50-98 – 86, вариант 7к.
   
3. 
   (32,010…32,018) мм; Р = 0,95. Измерение индикатором ИЧ 10 кл. точности 0 на стандартной стойке с настройкой по концевым мерам длины 3 кл. точности. Измерительное перемещение не более 0,1 мм; температурный режим измерений ± 2 ^оС.
   
4. 
   72,6360 мм; Δ_н= – 0,0012 мм, Δ_в= + 0,0018 мм, Релей; Р = 0,95.
   

_о

5. 
   10,75 м³/с; σ (Δ) = 0,11 м³/с, σ (Δ_с) = 0,18 м³/с, равн. Условия измерений: температура среды 20 ^оС, кинематическая вязкость измеряемого объекта 1,5·10 ^–6 м²/с.
   

В первом примере использована наиболее часто используемая форма: точечная оценка (8,334 г) с указанием симметричных границ погрешности измерений (± 0,012 г) и доверительной вероятности (0,95), с которой погрешность измерений не выходит за указанные границы. Распределение результатов наблюдений – нормальное (если в описании результата распределение не указано, то по умолчанию подразумевается нормальное распределение). Во втором примере представлена только точечная оценка, остальное определено ссылкой на аттестованную методику выполнения измерений, описанную в соответствующем документе.

В третьем примере точечная оценка и границы погрешности измерений не указаны, представлены границы интервала, который с выбранной доверительной вероятностью (0,95) накрывает истинное значение измеряемой величины. Отличительной особенностью четвертого примера является асимметричное распределение случайных погрешностей. Поэтому кроме точечной оценки (72,6360 мм) указаны асимметричные границы погрешности измерений – 0,0012 мм и + 0,0018 мм и вид распределения, поскольку он отличен от нормального. В описание результата включено и значение доверительной вероятности (0,95), с которой погрешность измерений не выходит за указанные границы. В пятом примере значение доверительной вероятности не указано, что можно рассматривать как формальное несоответствие требованиям обеспечения единства измерений. Однако противоречие не принципиальное, а скорее кажущееся, поскольку переход к оценке границ областей рассеяния случайной и неисключенной систематической составляющих погрешности измерений требует выбора доверительной вероятности. Расчет осуществляется через коэффициент Стьюдента t, а его значение зависит от числа степеней свободы и от выбранной доверительной вероятности, которая должна быть одинакова для обеих составляющих (случайной и неисключенной систематической составляющих погрешности). В качестве комментария следует сказать, что такая полная форма годится только для экзотических исследовательских ситуаций и непрактична в производственном употреблении, для которого желательна комплексная оценка погрешности измерения, например, полученная в результате компонирования двух описывающих составляющие погрешности функций в соответствии с ГОСТ 8.207. Можно предложить графическую интерпретацию результата измерений на числовой оси физической величины. Тогда для первого из приведенных примеров (8,334 ± 0,012) г; Р = 0,95 результат выглядит как показано на рисунке 8.1.

---

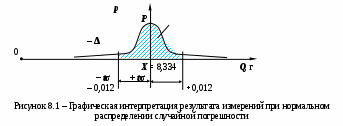
На оси физической величины Q указаны точечная оценка результата измерений (8,334 г) и границы погрешности (± 0,012) г. Для представления доверительной вероятности проводим ось ординат (ось плотности вероятности р) из точки, соответствующей точечной оценке результата измерений, и строим в полученной системе координат кривую нормального распределения результатов или погрешностей измерений. Из рисунка видно, что для увеличения доверительной вероятности (заштрихованной площади) Р необходимо расширить зону между границами погрешности измерений ± Δ. При фиксированном значении σ этого можно добиться только за счет увеличения коэффициента Стьюдента t. Зона между зафиксированными предельными значениями Х – Δ и Х + Δ с выбранной доверительной вероятностью Р накрывает истинное значение измеряемой физической величины, но поскольку фактически результат измерений представлен не в виде единичного значения, а как числовой интервал, принято говорить о «неопределенности измерений».

---

МОДУЛЬ 13. СРЕДСТВА ИЗМЕРЕНИЙ. МЕТРОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ СРЕДСТВ ИЗМЕРЕНИЙ

В РМГ 29 – 99 средства измерительной техники (измерительная техника) – обобщающее понятие, охватывающее технические средства, специально предназначенные для измерений. В примечании поясняется, что к средствам измерительной техники относят средства измерений и их совокупности (измерительные системы, измерительные установки), измерительные принадлежности, измерительные устройства.

Приведенное понятие подкрепляется набором терминов с определениями, которые не всегда удачны.

Измерительные принадлежности – вспомогательные средства, служащие для обеспечения необходимых условий для выполнения измерений с требуемой точностью. Приведенные в документе примеры включают термостат, специальные противовибрационные фундаменты, треногу для установки прибора по уровню и другие устройства, предназначенные для защиты объекта измерений и средств измерений от действия влияющих величин. В перечислении отсутствуют принадлежности к концевым мерам угла или длины, оправки, установочные призмы и иные технические средства, которые по технической сути значительно ближе к «принадлежностям».

Еще менее удачно определен термин измерительное устройство – часть измерительного прибора (установки или системы), связанная с измерительным сигналом и имеющая обособленную конструкцию и назначение. Устройство, входящее в технический комплекс, может иметь в определенной мере «обособленную конструкцию и назначение», и иметь информационные связи с другими техническими устройствами, но не «с измерительным сигналом». В качестве примеров измерительных устройств приведены регистрирующее устройство измерительного прибора (включающее ленту для записи, лентопротяжный механизм и пишущий элемент) и измерительный преобразователь, что существенно запутывает картину. Наиболее универсальным измерительным устройством в рамках данной концепции может считаться компьютер с периферией.

К средствам измерительной техники, непосредственно участвующим в получении и преобразовании измерительной информации относятся средства измерений.

Средство измерений – техническое средство, предназначенное для измерений, имеющее нормированные метрологические характеристики, воспроизводящее и (или) хранящее единицу физической величины, размер которой принимают неизменным (в пределах установленной погрешности) в течение известного интервала времени.

---

Основным признаком в данном определении являются нормированные метрологические характеристики, что подразумевает и возможность воспроизведения единицы физической величины с требуемой точностью, и ее сохранение на протяжении всего периода метрологической пригодности средства измерений.

В зависимости от функционального назначения и конструктивного исполнения различают такие виды средств измерений, как меры, измерительные преобразователи, измерительные приборы, индикаторы, измерительные установки, измерительные системы, измерительно-вычислительные комплексы.

Простейшим средством измерений является мера. Главная отличительная особенность меры – отсутствие каких-либо преобразований измерительной информации самим средством измерений. Мера физической величины (мера величины; мера) – средство измерений, предназначенное для воспроизведения и (или) хранения физической величины одного или нескольких заданных размеров, значения которых выражены в установленных единицах и известны с необходимой точностью.

Меры, предназначенные для воспроизведения физической величины заданного размера, называют однозначными, а воспроизводящие физические величины ряда размеров – многозначными. В качестве примеров однозначных мер можно назвать гирю (мера массы), угольник (мера прямого угла), плоскопараллельную концевую меру длины. К многозначным мерам следует отнести измерительную линейку, транспортир, измерительный сосуд, а также ступенчатый шаблон, угловую концевую меру с несколькими рабочими углами. Меры могут комплектоваться в наборы или конструктивно объединяться в так называемые «магазины».

Набор мер – комплект мер разного размера одной и той же физической величины, предназначенных для применения на практике как в отдельности, так и в различных сочетаниях (например, наборы концевых мер длины, угловых концевых мер, наборы разновесов). Магазин мер – набор мер, конструктивно объединенных в единое устройство, в котором имеются приспособления для их соединения в различных комбинациях (например, магазин электрических сопротивлений).

При оценивании величин по условным (неметрическим) шкалам, имеющим реперные точки, в качестве «меры» нередко выступают вещества или материалы с приписанными им условными значениями величин. Так, для шкалы твердости Мооса мерами являются минералы различной твердости. Приписанные им значения твердости образуют ряд реперных точек условной шкалы.

---