Файл: Лекции по теоретической метрологии.doc

Для того, чтобы некоторое свойство объекта можно было оценить по той или иной шкале, необходимо чтобы на множестве однотипных свойств объектов соблюдались определенные отношения. Поскольку мы предпочитаем объективную оценку свойства числом, то отношения на множестве свойства логичнее всего сопоставлять с аксиоматикой числа. Анализ соответствующих отношений позволит определить, какой тип шкалы применим для оцениваемых свойств объектов.


Таблица 2.1 – Сводные сведения о шкалах

Тип шкалы	Характеристика шкалы	Отношения, задаваемые на шкале	Математические операции с объектами шкал
Наименований	Числа или другие символы шкалы используются только для классификации исследуемых объектов	Эквивалентность	Накопление частот (для последующей статистической обработки)
Порядка	Можно установить, что свойство одного объекта находится в некотором соотношении со свойством другого объекта	Эквивалентность. Больше чем/меньше чем	Накопление частот, добавление постоянной, умножение на постоянную
Интервалов	Порядковая шкала с известными расстояниями между двумя любыми числами на шкале. Нулевая точка шкалы и оценочная единица выбираются произвольно	Эквивалентность. Больше чем/меньше чем. Определено отношение любых двух интервалов. Отношение координат любых двух точек шкалы зависит от выбранного нуля	Все операции с числами (после назначения нуля)
Отношений	Интервальная шкала с фиксированной нулевой точкой. Отношение любых двух координат шкалы фиксированное	Эквивалентность. Больше чем/меньше чем. Определено отношение любых интервалов и координат любых точек	Все операции с числами

Аксиоматику числа можно представить в виде трех групп аксиом:

АКСИОМЫ ТОЖДЕСТВА

1. Либо А = В, либо А ≠ В.

2. Если А = В, то В = А.

3. Если А = В, и В = С, то А = С.
АКСИОМЫ РАНГОВОГО ПОРЯДКА

4. Если А > В, то В < А

5. Если А > В и В > С, то А > C.
АКСИОМЫ АДДИТИВНОСТИ

6. Если А = С и В > 0, то А + В > С.

---

7. А + В = В + А.

8. Если А = С и В = D, то А + В = C + D.

9. (А + В) + С = А + (В + С).

Если на множестве объектов, которые характеризуются однородными рассматриваемыми свойствами, соблюдаются отношения свойств, определяемые аксиомами тождества, то эти объекты можно оценивать по шкале наименований. Если на множестве объектов соблюдаются отношения, определяемые аксиомами тождества и рангового порядка, эти объекты можно оценивать по шкале порядка. Если на множестве объектов соблюдаются отношения, определяемые полным набором аксиом, объекты можно оценивать по шкале интервалов или по шкале отношений. Разница в свойствах последних множеств, которая окончательно определяет вид применяемой шкалы, зависит от наличия или отсутствия фиксированного нуля на шкале.

Возможности применения различных шкалы для оценки однородных свойств объектов при соответствии отношений этих свойств определенному набору аксиом представлены в виде схемы ключевых понятий (СКП) на рисунке 2.7. Каждая из более мощных шкал включает в себя все предыдущие, что отражено на схеме системой «ящик в ящике».

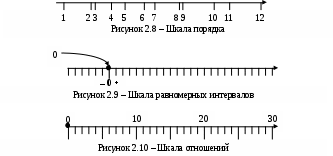
Графические отображения шкал порядка, интервалов и отношений представлены на рисунках 2.8…2.10. В их основу положены шкалы на осях ординат, полученные при построении шкал путем отображения интенсивности свойства с оси абсцисс на ось ординат в двухкоординатной системе (см. рисунки 2.4 – 2.6).



В метрологии, как и в любой другой научной области, используют все виды шкал. Шкалами наименований ограничиваются при классификации физических величин и других метрологических объектов, включая метрологические мероприятия и их результаты. Примерами шкал наименований могут быть наименования физических величин, наименования единиц физических величин (здесь множество пересекающихся шкал: полные обозначения, сокращенные обозначения русские и международные), шкала наименований параметров и характеристик «неопределенности» измерений.

Если на множестве объектов классификации проявляются топологические отношения между классифицируемыми свойствами, то можно говорить о развитии шкалы до уровня ранговой. Например, классификация средств измерений на эталоны, эталонные (образцовые) и рабочие средства получила дальнейшее развитие по характеристикам их точности. При построении поверочной схемы используют ранговые шкалы точности эталонов (распределение на первичные и вторичные эталоны) и эталонных (образцовых) средств измерений (распределение на разряды). Кроме того, достаточно часто применяют шкалы условных классов точности эталонных и рабочих средств измерений (например, классы нулевой, первый и второй). Разряды и ранжированные классы точности используются для реализации шкалы порядка, поскольку наименования уровней позволяет распределить объекты по точности. Очевидно, что прибор второго класса менее точен, чем однотипный прибор первого и точнее, чем третьего класса.

---

Кроме ранжированных классов точности средств измерений есть и «относительные» классы точности, которые характеризуют, например, значением относительной погрешности прибора в процентах. Эти классы составляют шкалу отношений: прибор класса точности 0,5 (относительная погрешность 0,5 %) в пять раз точнее аналогичного прибора класса 2,5 (относительная погрешность 2,5 %).

Шкалы порядка иногда применяют и для «количественной» оценки физических величин. Пример такой шкалы – используемая в минералогии шкала твердости Мооса, приведенная в таблице 2.2. Минералы условно разделяются на десять групп, расположенных в порядке возрастания твердости – от первой до десятой. Коэффициент твердости определяется так: если какой-либо минерал царапает, например, кальцит (твердость 3) и не царапает флюорит (твердость 4), то его твердость можно обозначить коэффициентом 3,5 (или другим значением между 3 и 4). Внутри каждого из указанных интервалов могут быть построены участки той же шкалы с более мелкой градацией.

Применяемые сегодня шкалы твердости Роквелла, Бринелля, Виккерса и другие тоже фактически являются окультуренными шкалами порядка, о чем свидетельствует отсутствие математических формул для перевода твердости из одних единиц в другие. Подобные трудности встречаются и при использовании разных шкал светочувствительности фотоматериалов. Отсутствие в таких шкалах фиксированной единицы ставит под сомнение соответствие их основному уравнению измерений. Однако такие шкалы даже с переменной единицей аппаратурно воспроизводятся при измерениях, поэтому их называют условными.


Таблица 2.2 – Шкала твердости (шкала Мооса)

1	Тальк
2	Гипс
3	Кальцит
4	Флюорит (плавиковый шпат)
5	Апатит
6	Ортоклаз (полевой шпат)
7	Кварц
8	Топаз
9	Корунд
10	Алмаз

Условная шкала «силы ветра» в баллах, предложенная английским адмиралом Фрэнсисом Бофортом в 1805 году, в соответствии с международным соглашением 1964 года рассматривается как шкала скорости ветра (таблица 2.3). На место условных баллов пришли аппаратурно измеряемые скорости в метрах в секунду или километрах в час.

---

Таблица 2.3 – Оценка скорости ветра (в сопоставлении со шкалой Бофорта)

Балл	Наименование «силы ветра»	Словесная характеристика	Скорость		«Цена» балла, м/с
			Vmin– Vmax, м/с	Vmax, км/ч
0	Штиль (безветрие)	Дым идет вертикально	0 – 0,9	3,24	0,9
1	Тихий ветер	Дым идет слегка наклонно	0,9 – 2,4	8,64	1,5
2	Легкий ветер	Ощущается лицом, шелестят листья	2,4 – 4,4	15,84	2,0
3	Слабый ветер	Развеваются флаги	4,4 – 6,7	24,12	2,3
4	Умеренный ветер	Поднимает пыль	6,7 – 9,3	33,48	2,6
5	Свежий ветер	Вызывает волны на воде	9,3 – 12,3	44,28	3,0
6	Сильный ветер	Свистит в вантах, гудят провода	12,3 – 15,6	56,16	3,3
7	Крепкий ветер	На волнах образуется пена	15,6 – 18,9	68,04	3,3
8	Очень крепкий ветер	Трудно идти против ветра	18,9 – 22,6	81,36	3,7
9	Шторм	Срывает черепицу	22,6 – 26,4	95,06	3,8
10	Сильный шторм	Вырывает деревья с корнем	26,4 – 30,5	109,80	4,1
11	Жестокий шторм	Большие разрушения	30,5 – 34,8	125,28	4,3
12	Ураган	Опустошительное действие	34,8 – 39,2	141,12	4,4

---

Есть и иные современные интерпретации шкалы Бофорта, с отличными значениями скоростей и балльных интервалов, что подтверждает невозможность строгой трансформации ранговой шкалы в интервальную.

Очевидно, что совершенствование знаний о физической величине или повышение строгости ее определения сопровождается построением более мощной шкалы. Примером эволюции шкал являются температурные шкалы. Создание шкал наименований базировалось на последовательном разделении понятий «температура» и «теплота», затем различении температуры как оценки степени нагретости тел и термодинамической температуры. Температура, которая когда-то оценивалась чисто топологически по шкале порядка (холодное-теплое-горячее), затем приобрела множество интервальных шкал с несовпадающими нулями и единицами (шкалы Реомюра, Фаренгейта, Цельсия), и, наконец, пришла к логически завершенной термодинамической шкале Кельвина с абсолютным нулем.

Для полноценных измерений физических величин фактически подходят только наиболее мощные шкалы (интервалов и отношений). Есть физические величины с фиксированным «естественным» нулем (масса, длина), а есть величины, которые никогда не будут иметь такого нуля (время, разность потенциалов), но для математической обработки результатов измерений существенно важно, что после фиксации нуля («естественного» или условного) интервалы физических величин полностью равноценны для приложения математического аппарата.

При наличии доступной исследователю шкалы, например воспроизводимой средством измерений, порядок измерения некоторого свойства (в том числе конкретной физической величины) можно представить следующим образом:

1. 
   Идентификация оцениваемого свойства (фиксация соответствующей объекту измерения шкалы наименований).
   
2. 
   Идентификация типа оценочной шкалы (порядка, интервалов, отношений).
   
3. 
   Фиксация положения оцениваемого свойства на шкале (оценка уровня интенсивности свойства)
   

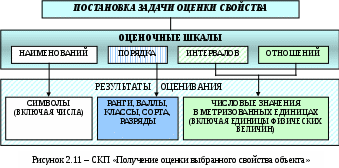
Схематически порядок получения оценки некоторого свойства объекта с применением шкал наименований, порядка, интервалов и отношений представлен на рисунке 2.11 (Схема ключевых понятий «получение оценки выбранного свойства объекта»).



В некоторых литературных источниках встречается понятие «измерение по шкале наименований» (по шкале наличия – отсутствия нежелательных свойств), которое нельзя признать корректным. Приводимые примеры шкал: «годное – брак», «устраивает – не устраивает», «присутствует – отсутствует» свидетельствуют об оценивании перехода свойства за некоторое пороговое значение на шкале порядка. Для аппаратурной реализации таких оценок в измерительных процедурах часто применяют индикаторы.

---