Оглавление


введение

Истоки проективной геометрии относятся к XV веку. Расцвет живописи в эпоху Возрождения вызвал появление теоретических исследований правил перспективы. Однако от первых шагов создания теории до того времени, когда эта теория оформилась в специальную науку прошло триста лет. Почему? Художники эпохи Возрождения не могли даже и догадаться насколько общи и значительны идеи и закономерности, заложенные в учении о перспективе, а требования техники были ограниченными, нужды в точном техническом черчении не было, тем более в его теоретическом обосновании.

Проективная геометрия - раздел геометрии, изучающий проективные плоскости и пространства. Главная особенность проективной геометрии состоит в принципе двойственности, который прибавляет изящную симметрию во многие конструкции. Проективная геометрия может изучаться как с чисто геометрической точки зрения, так с аналитической (с помощью однородных координат) и с алгебраической, рассматривая проективную плоскость как структуру над полем. Часто, и исторически, вещественная проективная плоскость рассматривается как Евклидова плоскость с добавлением «прямой в бесконечности». Проективная геометрия дополняет Евклидову, предоставляя красивые и простые решения для многих задач.

Каждый день человек в своей повседневной деятельности решает множество геометрических задач. На практике в большинстве случаев найти точное решение возникшей задачи с первого раза человеку не удается. Это происходит главным образом не потому, что мы не умеем этого сделать, а поскольку искомое решение обычно не выражается в привычных для нас элементарных или других известных действиях и методах. Та же проблема возникает при решении задач на проективной плоскости. Поэтому важное значение приобретает расширение знаний, умений и навыков решения геометрических задач на проективной плоскости и возможность применениях этих знаний в различных областях науки и техники, тем самым обуславливая актуальность данной темы исследования.

---

1. Проективная плоскость
   

1.1 Центральное проектирование

Первые шаги в направлении проективной геометрии были сделаны в 1639 г. французским архитектором Ж. Дезаргом и Б. Паскалем в 1640 году. Они изучали свойства фигур на евклидовой плоскости и в евклидовом пространстве, сохраняющиеся при центральных проектированиях.

Посмотрим, как осуществляется центральное проектирование. На рисунке 1 вы видите две плоскости  и , и точку , не лежащую в этих плоскостях.

Возьмем любую точку М, лежащую на плоскости . Проведем прямую ОМ и найдем M  (OM) , М´- проекция М (из центра О). Точке М поставим в соответствие ее проекцию из центра О. Между плоскостями  и  устанавливается соответствие, которое называется центральным проектированием.



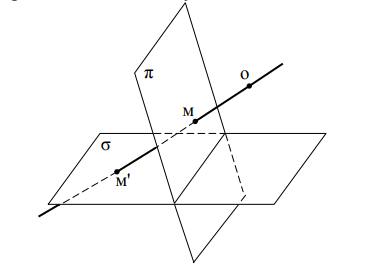
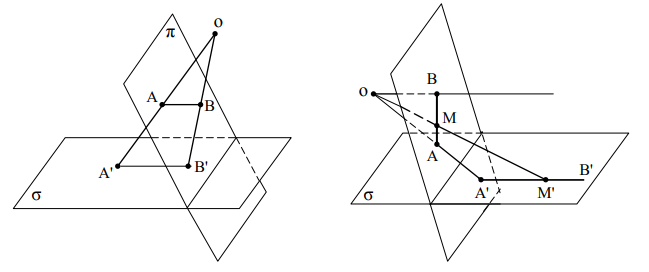
Рис.1 Рис. 2 Рис.3

Если на плоскости  будет задана фигура F, то множество проекций всех точек фигуры F на плоскости  называется проекцией фигуры F. Принимая за центр проектирования различные точки и меняя положение плоскости , мы будем получать различные проекции фигуры F. Например, проекцией отрезка АВ может быть отрезок А´В´ (рис. 2), луч А´В´ (рис. 3). Значит, понятие отрезка не сохраняется при центральных проектированиях. Проектируя окружность, можно получить эллипс, параболу и даже гиперболу (Рис. 4-6).



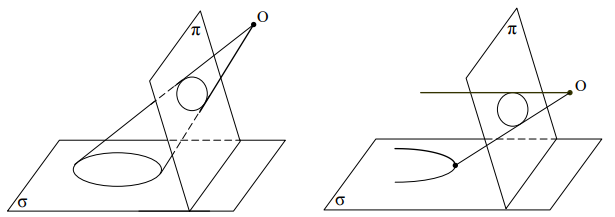
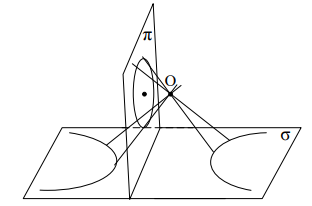
Рис. 4 Рис. 5 Рис. 6

С другой стороны, фигуры обладают свойствами, которые сохраняются при любом центральном проектировании и с фигурами можно связать величины, сохраняющиеся при любом проектировании. Такие свойства и величины называют инвариантами проектирования. Именно эти свойства фигур, инвариантные при любом центральном проектировании, французский геометр Ж. Понселе (1788–1867) назвал проективными свойствами и рассматривал их как объекты исследования в проективной геометрии. Например, прямая при центральном проектировании переходит в прямую (рис.7).

---

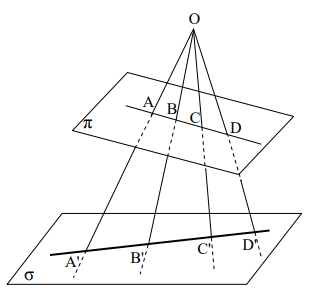
Рис. 7

Задача изучения проективных свойств фигур привлекала к себе внимание многих геометров, среди которых после Ж. Понселе следует назвать М. Шаля – французского геометра и швейцарского геометра Я. Штейнера. Однако, у Я. Штейнера и М. Шаля, как и у Ж. Понселе проективная геометрия выглядела как часть евклидовой геометрии. Превращение проективной геометрии в самостоятельную дисциплину было делом второй половины 19 века. Важной предпосылкой для этого превращения было введение так называемых несобственных (или бесконечно удаленных) геометрических элементов.

2. Пополнение плоскости
   

Чтобы получить наглядную интерпретацию проективной геометрии, мы рассмотрим модель расширенной (аффинно-проективной) плоскости.

Пусть О – произвольная точка пространства, П – некоторая плоскость, не проходящая через точку О. Тогда любая точка М плоскости П будет определять в пространстве прямую ОМ.

Ясно, как эту интерпретацию можно распространить до интерпретации всей расширенной плоскости: достаточно включить в рассмотрение и прямые, параллельные плоскости П (проходящие через точку О), считая, что каждая такая прямая изображает несобственную точку всех прямых плоскости П, параллельных этой прямой.

Определение. Множество, состоящее из всех точек рассматриваемой евклидовой плоскости и всех несобственных точек, называется проективной плоскостью.

Покажем следующее:

1.Через любые две различные точки проективной плоскости проходит и притом только одна прямая.

В самом деле, если эти две точки собственные, то существует и притом только одна прямая, проходящая через эти точки. Если одна из точек собственная, а другая – несобственная, то из пучка обыкновенных параллельных прямых, к каждой из которых присоединена эта несобственная точка, нужно выбрать ту, которая проходит через данную собственную точку.

Если, наконец, обе данные точки несобственные, то они по определению лежат на единственной несобственной прямой.

2.Любые две различные прямые проективной плоскости имеют и притом только одну общую точку.

В самом деле, если обе прямые собственные, то они соответствуют двум различным обыкновенным прямым; если эти прямые пересекаются, то данные проективные прямые имеют различные несобственные точки, значит указанная выше обыкновенная точка пересечения является единственной точкой, общей для двух данных проективных прямых. Если же обыкновенные прямые параллельны, то данные проективные прямые по определению имеют общую им обеим несобственную точку, и эта точка является единственной точкой, общей для данных прямых. Наконец, если одна из данных проективных прямых несобственная, а другая – собственная, то единственной их общей точкой является несобственная точка данной собственной прямой.

---

1.3 Связка как модель проективной плоскости

Определение. Связкой прямых и плоскостей с центром O в трехмерном пространстве называется множество всех прямых и плоскостей, проходящих через данную точку O. Обозначаться связка будет той же буквой O. Прямая связки инцидентна плоскости, если она в ней содержится, плоскость связки инцидентна прямой, если она через нее проходит.

Перспективное соответствие осуществляет взаимно однозначное отображение пополненной плоскости на связку, т.е. отображение точек пополненной плоскости на множество прямых связки, определяемое следующим образом. Рассмотрим пополняемую плоскость π как лежащую в трехмерном пространстве. Пусть точка O не принадлежит π и определяет связку. Каждой собственной точке π поставим в соответствие единственную прямую связки, проходящую через нее. Каждой несобственной точке π, т.е. направлению или несобственному пучку на π, поставим в соответствие единственную прямую связки, имеющую то же направление (Рис. 8).

Очевидно, что выполнены следующие условия.

1. При перспективном соответствии прямые переходят в плоскости и сохраняется отношение инцидентности. Поэтому прямые связки называют «точками», а плоскости – «прямыми» данной модели проективной плоскости.

2. При перспективном соответствии несобственная прямая переходит в плоскость связки, параллельную π. Таким образом, пополненная плоскость соответствует связке с выделенной плоскостью, а проективная плоскость – просто связке.



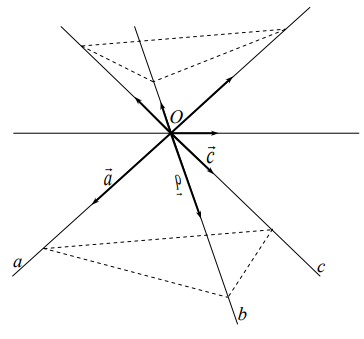
Рис. 8
1.4 Сфера как модель проективной плоскости

Рассмотрим сферу S² в евклидовом пространстве и связку прямых с центром в точке O. Каждая прямая связки пересекает сферу в двух точках. Чтобы установить взаимно однозначное соответствие между прямыми связки и точками сферы, отождествим диаметрально противоположные точки сферы. Построенный таким образом новый объект (Рис. 9) – сфера с отождествленными диаметрально противоположными точками. Она является моделью проективной плоскости. Это следует из того, что между прямыми связки и точками S² легко установить взаимно однозначное соответствие. А так как связка прямых евклидова пространства является моделью проективной плоскости, то и сфера с отождествленными диаметрально противоположными точками – модель проективной плоскости.

---

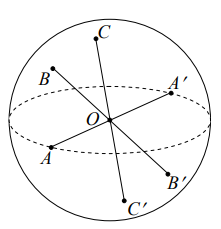
Рис. 9
1.5 Однородные координаты

Введем на евклидовой плоскости π общую декартову систему координат. Дополним эту плоскость несобственными точками до проективной плоскости П.

Возьмем на этой проективной плоскости собственную точку М. Пусть X и Y – ее координаты. Будем называть любую тройку чисел 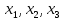однородными координатами точки М, если 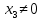и если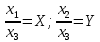



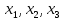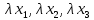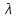Из этого определения следует, что если - однородные координаты собственной точки М проективной плоскости, то три числа , где – любое число, не равное нулю, также будут однородными координатами точки М.

Таким образом, однородные координаты собственной точки – это три числа из класса 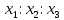всех пропорциональных между собой чисел, таких, что последнее число 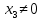. Это отмечают следующей записью: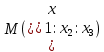



Например, запись М (1:2:-2) означает, что однородные координаты точки М – это числа 1, 2, -2, или 2, 4, -4, или -3, -6, 6, и т.д., аффинные же декартовы координаты этой точки X = -1/2, Y = -1.

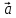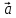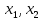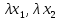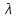Пусть теперь М – несобственная точка. Рассмотрим какой-нибудь вектор , не равный нулю и коллинеарный тем собственным прямым проективной плоскости, на которых лежит точка М. Обозначим координаты вектора через . Вектор с координатами , где – любое число, отличное от нуля, также ненулевой, коллинеарен вектору 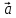и собственным прямым, на которых лежит несобственная точка М. Назовем любую тройку чисел из класса троек

---

Смотрите также файлы

• Отчет по лабораторной работе 100 Измерение электронным секундомером интервалов времени, задаваемых по механическому секундомеру.docx

• Институт ветеринарной медицины и биотехнологии кафедра ветеринарносанитарной экспертизы и паразитологии рабочая тетрадь.docx

• Дисциплина Психология развития и возрастная психология.doc

• Дисциплина Психология развития и возрастная психология.doc

• Контрольная работа по дисциплине Технология и оборудование автоматизированных сборочных производств Вариант 56.docx