ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 150
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
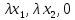однородными координатами несобственной точки М и будем писать: 
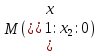
Итак, однородные координаты несобственной точки М – это любая тройка чисел из класса пропорциональных между собой троек
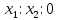, где 
– координаты какого-нибудь ненулевого вектора, коллинеарного собственным прямым, на которых лежит точка М.Теорема. Всякая прямая на проективной плоскости выражается однородным уравнением первой степени
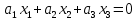
и обратно, всякое такое уравнение является уравнением прямой на проективной плоскости.
Пример. На расширенной прямой d задан проективный репер R = {A1, A2, E} построить точку M (2, 3) по ее координатам в этом репере.
Решение. Пусть V2 – векторное пространство порождающее прямую d : (V2\{ 0 }) = d . В роли V2 возьмем множество направленных отрезков с началом в точке O d. Обозначим B = {
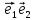} базис векторного пространства V2, согласованный с репером R. Решение задачи проводим по следующей схеме: 1. Восстановим векторный базис проективного репера R = {A1, A2, E}. Для этого возьмем любой вектор
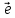, порождающий точку E и строим векторы 
,
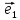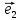, сумма которых дает вектор 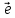. B = { 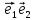} – векторный базис проективного репера. Векторы 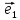, 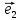порождают соответственно точки A1 и A2 (Рис.11). 2. Строим вектор
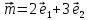.3. Строим точку M, порожденную вектором
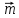, как пересечение прямых d и m, для которой вектор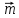
служит направляющим.
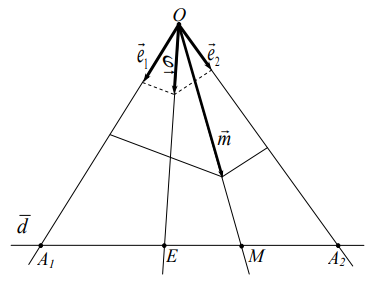
Рис.11
- Проективные преобразования
Определение. Проективное преобразование – это взаимно – однозначное отображение проективного пространства на себя, сохраняющее отношение порядка частично упорядоченного множества всех подмножеств.
Проективными преобразованиями на плоскости называются преобразования вида,
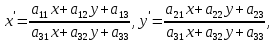
для которых
коэффициенты аij которых удовлетворяют условию, что три прямые
а11х + а12у + а13 = 0, а21x + а22y + а23 = 0 и а31x + а32y + а33 = 0
не пересекаются в одной точке.
При проективном преобразовании плоскости особую роль играет прямая L, определяемая уравнением a31x + a32y + a33 = 0. Для точек этой прямой знаменатели в выражениях для х ′ и y ′ обращаются в нуль, и поэтому данное преобразование не определено для точек этой прямой.
Отметим, что проективное преобразование инвариантно относительно выбора декартовой системы координат, так как формулы перехода от одной декартовой системы координат к другой линейны и поэтому при переходе к новой системе координат вид преобразований не меняется. Непосредственной проверкой можно убедиться, что последовательное проведение двух проективных преобразований является проективным преобразованием, тождественное преобразование и преобразование, обратное проективному, — также проективные преобразования. При проективных преобразованиях точки, лежащие на прямой, переходят в точки, также лежащие на прямой.
2.2 Проективные преобразования в пространстве
Проективными преобразованиями в пространстве называются преобразования вида
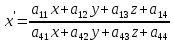
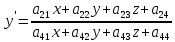
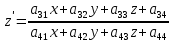
для которых четыре плоскости
а11х + а12y + а13z + а14 = 0,
а21х + а22y + а23z + а24 = 0,
а31х + а32y + а33z + а34 = 0,
а41х + а42у + а43z + а44 = 0
не пересекаются в одной точке.
Отметим, что проективное преобразование в пространстве не опре делено для точек плоскости, определяемой уравнением
a41х + а42у + а43z + а44 = 0.
Непосредственной проверкой можно убедиться, что последовательное проведение двух проективных преобразований, тождественное преобразование и преобразование, обратное проективному, — также проективные преобразования. При проективных преобразованиях точки, лежащие в одной плоскости, переходят в точки, также лежащие в одной плоскости, а точки, лежащие на прямой, переходят в точки, лежащие на прямой. Основным инвариантом проективного преобразования в пространстве является сложное отношение (ABCD)=(АСВ) : (ADB) любых четырех точек А, В, С и D на прямой.
2.3 Проективные отображения прямой
Подобно тому, как проективная плоскость находится в естественном взаимно однозначном (перспективном) соответствии со связкой, так проективная прямая находится в естественном соответствии с пучком прямых.
Пусть в самом деле на какой-нибудь плоскости π, проходящей через данную прямую d, взята точка О, не лежащая на прямой d (Рис. 12). Прямые m, проходящие через точку О, образуют пучок, который будем обозначать одной буквой О. Каждой точке M прямой d соответствует единственный ведущий в нее луч m = OM пучка О, и этим установлено соответствие, называемое перспективным, между точками M прямой d и лучами m пучка О.
Это соответствие взаимно однозначно, если считать, что лучу пучка О, параллельному прямой d, соответствует несобственная точка этой последней.
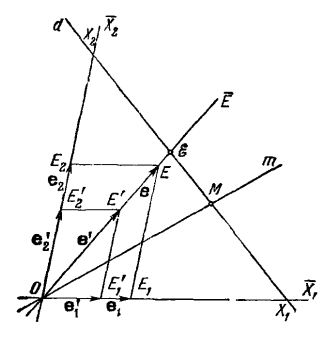
Рис. 12
Всякая аффинная система координат Oe1e2 на плоскости π, начало которой лежит в точке О пучка О, называется системой координат в пучке; координатами данного луча пучка называются координаты любого направляющего вектора этого луча, относительно системы Oe1e2. Две координатные системы Oe1e2 и Oe1e2 называем эквивалентными, если при некотором λ ≠ 0 имеем e
1 = λe1, e2 = λe2.
Через две различные точки
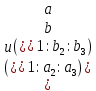проходит и притом только одна прямая, уравнение которой можно записать в виде: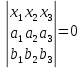
Написанное уравнение является однородным уравнением первой степени относительно
. Координаты этой прямой: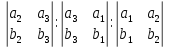
Если
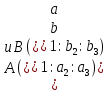– две различные точки проективной плоскости, то при любых α и β, не равных 0 одновременно, точка М с координатами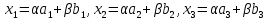
лежит на прямой АВ и, обратно, координаты любой точки прямой АВ могут быть представлены в таком виде.
2.4 Ангармоническое отношение
Рассмотрим проективную плоскость, на которой возьмем собственную прямую, а на ней упорядоченную четверку попарно различных собственных точек: A, B, C, D. Сложным, или ангармоническим, отношением (ABCD) точек A, B, C, D, взятых в этом порядке, называют число, определяемое равенством
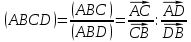
Если точки A и С совпадают или точки D и B совпадают, то считаем (ABCD) = 0. Если точка D совпадает с точкой A или точка С совпадает с точкой B, то (ABCD) не определяется.
Если одна из точек, например, точка D, несобственная, то по определению (ABCD) принимается равным пределу сложного отношения (ABCD1), где D1 – собственная точка, причем предел берется в предположении, что точка D1 неограниченно удаляется по прямой ABC.
Так как
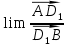при этом условии равен -1, то в случае, если D – несобственная точка,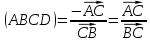 
Аналогично, если A – несобственная точка, то
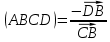, если B – несобственная точка, то 
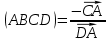, и, наконец, если C – несобственная точка, то 
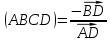.Определение сложного отношения четырех несобственных точек дано ниже.
Будем говорить, что ряд точек A, B, C, D, E, …, лежащих на одной прямой l, перспективен ряду прямых a, b, c, d, e, … пучка с центром O, не лежащем на прямой l, если прямые a, b, c, d, e, … проходят соответственно через точки A, B, C, D, E, …
Сложным, или ангармоническим, отношением (abcd) четырех попарно различных прямых a, b, c, d одного пучка с центром O назовем сложное отношение (ABCD) четырех точек A, B, C, D, лежащих на собственной прямой l, не проходяще через точку O, и перспективных прямым a, b, c, d (в случае, если совпадают прямые a и с или d и b, считаем (abcd) = 0, если прямая d совпадает с a или прямая c c b, то (abcd) не определяется).
Теорема. Сложное отношение четырех точек и сложное отношение четырех прямых не меняются при проективном преобразовании.
Доказательство. Достаточно, очевидно, доказать первую часть теоремы. Рассмотрим две произвольные точки: A(x1:x2:x3), B(y1:y2:y3).
Возьмем на прямой AB две точки:
С((αx1+βy1):(αx2+βy2):(αx3+βy3)),
D((λx1+µy1):( λx2+µy2):( λx3+µy3)),
такие, что точки C и B различны, точки D и A также различны. Тогда
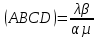
Произведем проективное преобразование
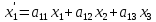
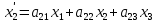
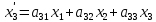
Пусть A (x1:x2:x3), B (y1:y2:y3) образы точек A и B при этом преобразовании. Тогда образами точек C и D в силу данных соотношений будут точки:
С ((αx1+βy1):(αx2+βy2):(αx3+βy3)),
D((λx1+µy1):( λx2+µy2):( λx3+µy3)).
Отсюда
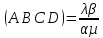=(ABCD).2.5 Принцип двойственности
На проективной плоскости и в пространстве справедлив принцип двойственности. Сформулируем принцип двойственности для проективной плоскости. Если на проективной плоскости справедливо некоторое предложение А, в котором идет речь о точках прямых и их взаимной принадлежности, то будет справедливо предложение А, которое получается из утверждения А путем замены слова «точка» на слово «прямая»: «прямая» – «точка»; «лежит на» – «проходит через», «проходит через» – «лежит на». Например: Предложение А: Через любые две точки проективной плоскости проходит единственная прямая. Двойственное ему предложение А: Любые две прямые пересекаются в одной точке.