ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 149
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Рассмотрим далее теорему Дезарга и проиллюстрируем на ней применение принципа двойственности.
2.6 Теорема Дезарга
Теорема Дезарга (и её модификации) является одной из центральных теорем проективной геометрии, описывающей отношение «принадлежности» между точками и прямыми. Она позволяет легко решать задачи на доказательство принадлежности трех точек одной прямой, принадлежности трех прямых одному пучку, задачи на построение. На проективной плоскости теорема Дезарга формулируется для двух трехвершинников.
Теорема. Пусть даны два треугольника ABC и ABC. Если три прямые AA, BB, CC, проходят через одну точку, то точки пересечения прямых
а a, b b, c c лежат на одной прямой (Рис. 13).
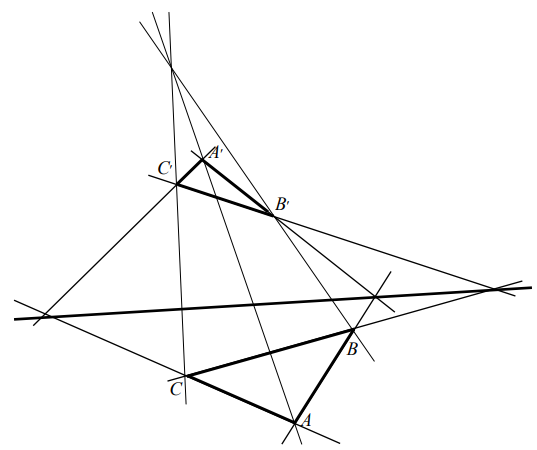
Рис. 13
Доказательство. Доказательство теоремы не является тривиальным, несмотря на всю простоту чертежа, состоящего только из прямых линий. Теорема явственно принадлежит проективной геометрии, так как при проектировании рассматриваемый чертеж не теряет свойств, упомянутых в теореме. Теорема Дезарга справедлива также и в том предположении, что рассматриваемые треугольники расположены в двух различных (непараллельных) плоскостях и что подобного рода «трехмерная» или «пространственная» теорема Дезарга доказывается без малейших затруднений.
По предположению, прямые AA, BB и CC пересекаются в одной и той же точке О (Рис. 14). В таком случае прямые AB и AB лежат водной плоскости и, значит, пересекаются в некоторой точке R; пусть, таким же образом, AC и AC пересекаются в точке Q, а BC и BC - в точке P. Так как точки P, Q и R находятся на продолжениях сторон треугольников ABC и ABC, то все они лежат в плоскости каждого из этих треугольников и потому – на прямой пересечения этих двух плоскостей. Значит P, Q и R – коллинеарны, что и требовалось доказать.
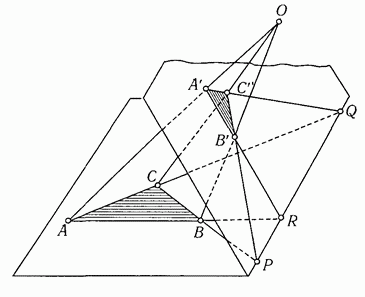
Рис. 14
Сформулируем теорему обратную теореме Дезарга
Даны два треугольника и никакие их вершины, и стороны не совпадают. Тогда, если точки пересечения соответственных сторон а a, b b, c c этих треугольников лежат на одной прямой, то прямые AA, BB, CC, проходящие через соответственные вершины треугольников, пересекаются в одной точке.
Дополняя евклидову плоскость несобственными точками, мы получим расширенную плоскость, которая является моделью проективной плоскости. Значит, для решения задач евклидовой геометрии можем использовать факты проективной геометрии, в частности, теорему Дезарга на расширенной евклидовой плоскости.
Заключение
Созданная в середине XIX века проективная геометрия и сегодня сохранила свое значение в качестве важной модели, используемой в самых разных разделах чистой и прикладной математики.
Источником ее создания явились потребности графики, архитектуры, развитие теории изображений в перспективе.
Неевклидовая геометрия ясно продемонстрировала, что математику нельзя более рассматривать, как свод непререкаемых истин. Математики обрели свободу исследовать любые идеи, которые могли показаться им привлекательными, и позволившие в дальнейшем рассмотреть различные геометрические системы.
Развитие аналитических методов обычной проективной геометрии и построение на этой базе комплексной проективной геометрии поставили задачу о зависимости тех или иных проективных свойств.
список литературы
-
Александров П. С. Лекции по аналитической геометрии. – М.: Наука -
Моденов С. М. Аналитическая геометрия. – М.: Изд. МГУ -
Постников М. М. Аналитическая геометрия. – М.: Наука -
Ефимов Н.И. Краткий курс аналитической геометрии.–М.:Физматлит -
Кадомцев С. В. Аналитическая геометрия и линейная алгебра. – М.: Физматлит -
Ильин В. А., Позняк Э. Г. Аналитическая геометрия. Учебник для вузов. – М.: Физматлит -
Троицкий Е. В. Конспект лекций по аналитической геометрии -
Горшкова Л.С. Проективная геометрия. Учебное пособие -
Р. Хартсхорн Основы проективной геометрии -
Игнатьева Ю. Г. Проективная геометрия и методы изображения