Файл: Методические указания и контрольные задания для студентовзаочников инженернотехнических и технологических специальностей вузов.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 259
Скачиваний: 8
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
КОНТРОЛЬНАЯ РАБОТА № 1

тела изменение его координаты со временем происходит по закону х= 10 + 5/- Юг2? Масса тела 2 кг.
-
Найти закон движения тела массой 1 кг под действием постоянной силы 10 Н, если в момент /=0 тело покоилось в начале координат (х=0).
-
Найти закон движения тела массой 1 кг под действием
1. Под действием какой силы при прямолинейном движении постоянной силы 1 Н, если в момент /=0 начальная координата х=0 и v0 = 5 м/с.
-
Найти закон движения тела массой 1 кг под действием постоянной силы 2 I I, если в момент /=0 имеем х0 = 1 и г>0=2 м/с.
-
Тело массой 2 кг движется с ускорением, изменяющимся по закону a=5t—10. Определить силу, действующую на тело через 5 с после начала действия, и скорость в конце пятой секунды.
-
Сплошной шар массой 1 кг и радиусом 5 см вращается вокруг оси, проходящей через его центр. Закон вращения шара выражается уравнением ^ = 10 + 5/—2/2. В точке, наиболее удаленной от оси вращения, на шар действует сила, касательная к поверхности. Определить эту силу и тормозящий момент.
-


секунды.
8. Материальная точка движется по окружности, радиус которой 20 м. Зависимость пути, пройденного точкой, от времени выражается уравнением 5=/3+4/2 —/+8. Определить пройденный путь, угловую скорость и угловое ускорение точки через 3 с от начала ее движения.
-
Материальная точка движется по окружности радиуса 1 м согласно уравнению 5=8/—0,2/3. Найти скорость, тангенциальное, нормальное и полное ускорение в момент времени 3 с.
-
Тело вращается равноускоренно с начальной угловой скоростью 5 с 1 и угловым ускорениемм 1 с-2. Сколько оборотов сделает тело за 10 с?
Автомобиль движется по закруглению шоссе, имеющему радиус кривизны 100 м. Закон движения автомобиля выражается уравнением 5= 100+10/—0,5/2. Найти скорость автомобиля, его тангенциальное, нормальное и полное ускорение в конце пятой
-
Параллелепипед размером 2x2x4 см3 движется параллельно большему ребру. При какой скорости движения он будет казаться кубом.
-
Какую скорость должно иметь движущееся тело, чтобы его продольные размеры уменьшились в два раза?
-
я-мезон — нестабильная частица. Собственное время жизни его 2,6 • 10“8 с. Какое расстояние пролетит я-мезон до распада, если он движется со скоростью 0,9 с?
-
Найти собственное время жизни нестабильной частицы /х-мезона, движущегося со скоростью 0,99 с, если расстояние, пролетаемое им до распада, равно 0,1 км.
-
Собственное время жизни л-мезона 2,6 • 10”8 с. Чему равно время жизни л-мезона для наблюдателя, относительно которого эта частица движется со скоростью 0,8 с?
-
Электрон, скорость которого 0,9 с, движется навстречу протону, имеющему скорость 0,8 с. Определить скорость их относительного движения.
-
Радиоактивное ядро, вылетевшее из ускорителя со скоростью 0,8 с, выбросило в направлении своего движения /3-частицу со скоростью 0,7 с относительно ускорителя. Найти скорость частицы относительно ядра.
-
Две частицы движутся навстречу друг другу со скоростью 0,8 с. Определить скорость их относительного движения.
-
При какой скорости движения релятивистское сокращение длины движущегося тела составит 25%.
-
Какую скорость должно иметь движущееся тело, чтобы его продольные размеры уменьшились на 75%.
-
Сплошной цилиндр массой 0,1 кг катится без скольжения с постоянной скоростью 4 м/с. Определить кинетическую энергию цилиндра, время до его остановки, если на него действует сила трения 0,1 Н.
-
Сплошной шар скатывается по наклонной плоскости, длина которой 1 м и угол наклона 30°. Определить скорость шара в конце наклонной плоскости. Трение шара о плоскость не учитывать.
-
Полый цилиндр массой 1 кг катится по горизонтальной поверхности со скоростью 10 м/с. Определить силу, которую необходимо приложить к цилиндру, чтобы остановить его на пути 2 м.
-
Маховик, имеющий форму диска массой 10 кг и радиусом 0,1 м, был раскручен до частоты 120 мин \ Под действием силы трения диск остановился через 10 с. Найти момент сил трения, считая его постоянным.
-
Обруч и диск скатываются с наклонной плоскости, составляющей угол 30° с горизонтом. Чему равны их ускорения в конце спуска? Силой трения пренебречь.
-
С покоящимся шаром массой 2 кг сталкивается такой же шар, движущийся со скоростью 1 м/с. Вычислить работу, совершенную вследствие деформации при прямом центральном неупругом ударе.
-
Масса снаряда 10 кг, масса ствола орудия 500 кг. При выстреле снаряд получает кинетическую энергию 1,5 • 10б Дж. Какую кинетическую энергию получает ствол орудия вследствие отдачи?
-
Конькобежец массой 60 кг, стоя на коньках на льду, бросает в горизонтальном направлении камень массой 2 кг со скоростью 10 м/с. На какое расстояние откатится при этом конькобежец, если коэффициент трения коньков о лед 0,02.
-
Молекула водорода, двигающаяся со скоростью 400 м/с, подлетает к стенке сосуда под углом 60° и упруго ударяется о нее. Определить импульс, полученный стенкой. Принять массу молекул равной 3 • 10
27 кг.Найти закон движения тела массой 1 кг под действием постоянной силы 10 Н, если в момент /=0 тело покоилось в начале координат (х=0).
Найти закон движения тела массой 1 кг под действием
Найти закон движения тела массой 1 кг под действием постоянной силы 2 I I, если в момент /=0 имеем х0 = 1 и г>0=2 м/с.
Тело массой 2 кг движется с ускорением, изменяющимся по закону a=5t—10. Определить силу, действующую на тело через 5 с после начала действия, и скорость в конце пятой секунды.
Сплошной шар массой 1 кг и радиусом 5 см вращается вокруг оси, проходящей через его центр. Закон вращения шара выражается уравнением ^ = 10 + 5/—2/2. В точке, наиболее удаленной от оси вращения, на шар действует сила, касательная к поверхности. Определить эту силу и тормозящий момент.


секунды.
8. Материальная точка движется по окружности, радиус которой 20 м. Зависимость пути, пройденного точкой, от времени выражается уравнением 5=/3+4/2 —/+8. Определить пройденный путь, угловую скорость и угловое ускорение точки через 3 с от начала ее движения.
-
Материальная точка движется по окружности радиуса 1 м согласно уравнению 5=8/—0,2/3. Найти скорость, тангенциальное, нормальное и полное ускорение в момент времени 3 с. -
Тело вращается равноускоренно с начальной угловой скоростью 5 с 1 и угловым ускорениемм 1 с-2. Сколько оборотов сделает тело за 10 с?
Параллелепипед размером 2x2x4 см3 движется параллельно большему ребру. При какой скорости движения он будет казаться кубом.
Какую скорость должно иметь движущееся тело, чтобы его продольные размеры уменьшились в два раза?
я-мезон — нестабильная частица. Собственное время жизни его 2,6 • 10“8 с. Какое расстояние пролетит я-мезон до распада, если он движется со скоростью 0,9 с?
Найти собственное время жизни нестабильной частицы /х-мезона, движущегося со скоростью 0,99 с, если расстояние, пролетаемое им до распада, равно 0,1 км.
Собственное время жизни л-мезона 2,6 • 10”8 с. Чему равно время жизни л-мезона для наблюдателя, относительно которого эта частица движется со скоростью 0,8 с?
Электрон, скорость которого 0,9 с, движется навстречу протону, имеющему скорость 0,8 с. Определить скорость их относительного движения.
Радиоактивное ядро, вылетевшее из ускорителя со скоростью 0,8 с, выбросило в направлении своего движения /3-частицу со скоростью 0,7 с относительно ускорителя. Найти скорость частицы относительно ядра.
Две частицы движутся навстречу друг другу со скоростью 0,8 с. Определить скорость их относительного движения.
При какой скорости движения релятивистское сокращение длины движущегося тела составит 25%.
Какую скорость должно иметь движущееся тело, чтобы его продольные размеры уменьшились на 75%.
Сплошной цилиндр массой 0,1 кг катится без скольжения с постоянной скоростью 4 м/с. Определить кинетическую энергию цилиндра, время до его остановки, если на него действует сила трения 0,1 Н.
Сплошной шар скатывается по наклонной плоскости, длина которой 1 м и угол наклона 30°. Определить скорость шара в конце наклонной плоскости. Трение шара о плоскость не учитывать.
Полый цилиндр массой 1 кг катится по горизонтальной поверхности со скоростью 10 м/с. Определить силу, которую необходимо приложить к цилиндру, чтобы остановить его на пути 2 м.
Маховик, имеющий форму диска массой 10 кг и радиусом 0,1 м, был раскручен до частоты 120 мин \ Под действием силы трения диск остановился через 10 с. Найти момент сил трения, считая его постоянным.
Обруч и диск скатываются с наклонной плоскости, составляющей угол 30° с горизонтом. Чему равны их ускорения в конце спуска? Силой трения пренебречь.
С покоящимся шаром массой 2 кг сталкивается такой же шар, движущийся со скоростью 1 м/с. Вычислить работу, совершенную вследствие деформации при прямом центральном неупругом ударе.
Масса снаряда 10 кг, масса ствола орудия 500 кг. При выстреле снаряд получает кинетическую энергию 1,5 • 10б Дж. Какую кинетическую энергию получает ствол орудия вследствие отдачи?
Конькобежец массой 60 кг, стоя на коньках на льду, бросает в горизонтальном направлении камень массой 2 кг со скоростью 10 м/с. На какое расстояние откатится при этом конькобежец, если коэффициент трения коньков о лед 0,02.
Молекула водорода, двигающаяся со скоростью 400 м/с, подлетает к стенке сосуда под углом 60° и упруго ударяется о нее. Определить импульс, полученный стенкой. Принять массу молекул равной 3 • 10
Стальной шарик массой 50 г упал с высоты 1 м на большую плиту, передав ей импульс силы, равный 0,27 Н • с. Определить количество теплоты выделевшегося при ударе и высоту, на которую поднимается шарик.
С какой скоростью движется электрон, если его кинетическая энергия 1,02 МэВ? Определить импульс электрона.
Кинетическая энергия частицы оказалась равной ее энергии покоя. Какова скорость этой частицы?
Масса движущегося протона 2,5 * 10“27 кг. Найти скорость и кинетическую энергию протона.
Протон прошел ускоряющую разность потенциалов в 200 МВ. Во сколько раз его релятивистская масса больше массы покоя? Чему равна скорость протона?
Определить скорость электрона, если его релятивистская масса в три раза больше массы покоя. Вычислить кинетическую и полную энергию электрона.
Вычислить скорость, полную и кинетическую энергию протона в тот момент, когда его масса равна массе покоя «-частицы.
Найти импульс, полную и кинетическую энергию электрона, движущегося со скоростью, равной 0,7 с.
Протон и а-частица проходят одинаковую ускоряющую разность потенциалов, после чего масса протона составила половину массы покоя а-частицы. Определить разность потенциалов.
Найти импульс, полную и кинетическую энергию нейтрона, движущегося со скоростью 0,6 с.
Во сколько раз масса движущегося дейтрона больше массы движущегося электрона, если их скорости соответственно равны 0,6 с и 0,9 с. Чему равны их кинетические энергии.
Найти среднюю кинетическую энергию вращательного движения всех молекул, содержащихся в 0,20 г водорода при температуре 27 °C.
Давление идеального газа 10 мПа, концентрация молекул 2 • 1012 см 3. Определить среднюю кинетическую энергию поступательного движения одной молекулы и температуру газа.
Определить среднее значение полной кинетической энергии одной молекулы аргона и водяного пара при температуре 500 К.
Средняя кинетическая энергия поступательного движения молекул газа равна 15*10 21 Дж. Концентрация молекул равна 9 * 1019 см 3. Определить давление газа.
В баллоне емкостью 50 л находится сжатый водород при 27 °C. После того как часть воздуха выпустили, давление понизилось на 1 • 105 Па. Определить массу выпущенного водорода. Процесс считать изотермическим.
В сосуде, имеющем форму шара, радиус которого 0,1 м, находится 5,6 г азота До какой температуры можно нагреть сосуд, если его стенки выдерживают давление 5 • 105 Па?
При температуре 300 К и давлении 1,2 105 Па плотность смеси водорода и азота 1 кг/м3. Определить молярную массу смеси.
В баллоне емкостью 0,8 м3 находится 2 кг водорода и 2,9 кг азота. Определить давление смеси, если температура окружающей среды 27 °C.
До какой температуры можно нагреть запаянный сосуд, содержащий 36 г воды, чтобы он не разорвался, если известно, что стенки сосуда выдерживают давление 5 * 106 Па. Объем сосуда 5 л.
При температуре 27 °C и давлении 106 Па плотность
_ г Л
смеси кислорода и азота 12 —х. Определить молярную массу дм
смеси.
-
В сосуде емкостью 1 л содержится кислород массой 32 г. Определить среднее число соударений молекул в секунду при температуре 100 К. -
Определить среднюю длину и среднюю продолжительность свободного пробега молекул углекислого газа при температуре 400 К и давлении 1,38 Па. -
В сосуде емкостью 1 л находится 4,4 г углекислого газа. Определить среднюю длину свободного пробега молекул. -
Определить коэффициент диффузии гелия при давлении 1 • 106 Па и температуре 27 °C. -
Определить коэффициент внутреннего трения кислорода при температуре 400 К. -
В сосуде емкостью 5 л содержится 40 г аргона. Определить среднее число соударений молекул в секунду при температуре 400 К. -
Определить коэффициент внутреннего трения воздуха при температуре 100 К. -
Определить коэффициент диффузии азота при давлении 0,5 105 Па и температуре 127 °C. -
Коэффициент внутреннего трения кислорода при нормальных условиях 1,9 10 “4 кг/м 1 с. Определить коэффициент теплопроводности кислорода. -
Коэффициент диффузии водорода при нормальных условиях 9,1 10 5 м2/с. Определить коэффициент теплопроводности водорода. -
Определить, какое количество теплоты необходимо сообщить аргону массой 400 г, чтобы нагреть его на 100 К: а) при постоянном объеме; б) при постоянном давлении. -
Во сколько раз увеличится объем 2 молей кислорода при изотермическом расширении при температуре 300 К, если при этом газу сообщили 4 кДж теплоты. -
Какое количество теплоты нужно сообщить 2 молям воздуха, чтобы он совершил работу в 1000 Дж: а) при изотермическом процессе; б) при изобарическом процессе. -
Найти работу и изменение внутренней энергии при адиабатном расширении 28 г азота, если его объем увеличился в два раза. Начальная температура азота 27 °C. -
Кислород, занимающий объем 10 л и находящийся под давлением 2*10^ Па, адиабатно сжат до объема 2 л. Найти работу сжатия и изменение внутренней энергии кислорода. -
Определить количество теплоты, сообщенное 88 г углекислого газа, если он был изобарически нагрет от 300 К до 350 К. Какую работу при этом может совершить газ и как изменится его внутренняя энергия? -
При каком процессе выгоднее производить расширение воздуха: изобарическом или изотермическом, если объем увеличивается в пять раз. Начальная температура газа в обоих случаях одинаковая. -
При каком процессе выгоднее производить нагревание 2 молей аргона на 100 К: а) изобарическом; б) изохорическом. -
Азоту массой 20 г при изобарическом нагревании сообщили 3116 Дж теплоты. Как изменилась температура и внутренняя энергия газа. -
При изотермическом расширении одного моля водорода была затрачена теплота 4 кДж, при этом объем водорода увеличился в пять раз. При какой температуре протекает процесс? Чему равно изменение внутренней энергии газа, какую работу совершает газ? -
Определить изменение энтропии 14 г азота при изобарном нагревании его от 27 °C до 127 °C. -
Как изменится энтропия 2 молей углекислого газа при изотермическом расширении, если объем газа увеличивается в четыре раза. -
Совершая цикл Карно, газ отдал холодильнику 0,65 теплоты, полученной от нагревателя. Определить температуру холодильника, если температура нагревателя 400 К. -
Тепловая машина работает по оциклу Карно, к.п.д. которого 0,4. Каков будет к.п.д. этой машины, если она будет совершать тот же цикл в обратном направлении?
-
Холодильная машина работает по обратному циклу Карно, к.п.д. которого 400%. Каков будет к.п.д. этой машины, если она работает по прямому циклу Карно. -
При прямом цикле Карно тепловая машина совершает работу 1000 Дж. Температура нагревателя 500 К, температура холодильника 300 К. Определить количество теплоты, получаемое машиной от нагревателя. -
Найти изменение энтропии при нагревании 2 кг воды от 0 до 100 °C и последующем превращении ее в пар при той же температуре. -
Найти изменение энтропии при плавлении 2 кг свинца и дальнейшем его охлаждении от 327 до 0 °C. -
Определить изменение энтропии, происходящее при смешивании 2 кг воды, находящихся при температуре 300 К, и 4 кг воды при температуре 370 К. -
Лед массой 1 кг, находящийся при температуре 0 °C, нагревают до температуры 57 °C. Определить изменение энтропии.
II. ОСНОВЫ ЭЛЕКТРОДИНАМИКИ
ПОЯСНЕНИЯ К РАБОЧЕЙ ПРОГРАММЕ
Изучение электрических и магнитных явлений было проведено в XIX в. Эти явления связаны с особой формой существования материи —■ электромагнитным полем. Электромагнитные взаимодействия не только объясняют все электромагнитные явления, но и обеспечивают силы, обусловливающие существование вещества на атомном и молекулярном уровнях как целого. Важность теории электромагнитного поля связана с тем, что она включает всю оптику, так как свет представляет собой электромагнитное излучение. Основой теории электромагнитного поля является теория Максвелла. Уравнения Максвелла установили тесную связь между электрическими и магнитными явлениями, которые раньше рассматривались как независимые. Максвелл сформулировал такое важнейшее понятие физики, как электромагнитное поле.
Изучение основ электродинамики начинается с электрического поля в вакууме. Эта тема является фундаментом раздела, включающего электростатику и постоянный ток. Особое внимание при изучении этого раздела следует обратить на закон сохранения электрического заряда, инвариантность его в теории относительности, на силовую и энергетическую характеристики поля (напряженность, потенциал) и связь между ними. Студент должен уметь применять теорему Остроградского — Гаусса для вычисления напряженности электрических полей и уяснить такие понятия, как поток и циркуляция вектора напряженности поля.
При изучении электрического поля в диэлектриках следует представлять механизм поляризации полярных и неполярных диэлектриков и преимущество вектора электрического смещения перед вектором напряженности для описания электрического поля в неоднородных диэлектриках.
При изучении вопроса об энергии заряженных проводников и конденсаторов студент должен обратить внимание, что в рамках электростатики нельзя однозначно решить вопрос о локализации этой энергии. С равным правом можно считать, что энергией обладают как заряженные проводники, так и создаваемое ими электрическое поле.
Изучение темы «Постоянный электрический ток» следует начать с классической электронной теории проводимости металлов, на ее основе рассмотреть законы Ома и Джоуля — Ленца. Четко разграничить такие понятия, как разность потенциалов, электродвижущая сила и электрическое напряжение.
Изучая раздел «Магнитное поле», студент должен уделить особое внимание закону Ампера, знать и уметь применять закон Био — Савара — Лапласа для расчета магнитной индукции или напряженности магнитного поля прямолинейного и кругового токов, а также закон полного тока (циркуляция вектора магнитной индукции) для расчета магнитного поля тороида и длинного соленоида. При изучении вопроса, связанного с действием магнитного поля на движущиеся заряды, нужно уметь применять силу Лоренца для определения направления движения заряженных частиц в магнитном поле, представлять себе принцип действия циклических ускорителей заряженных частиц, а также определять работу перемещения проводника и контура с током в магнитном поле.
При изучении явления электромагнитной индукции необходимо усвоить, что механизм возникновения ЭДС индукции имеет электронный характер. Изучив основной закон электромагнитной индукции Фарадея — Максвелла, студент на его основе должен уметь вывести и применять для расчетов формулы электродвижущей силы индукции, энергии магнитного поля.
Изучение магнитных свойств вещества носит, в основном, описательный характер. Студент при этом должен уяснить, что исходя из выражения циркуляции вектора магнитной индукции, магнитное поле, в отличие от электрического, является вихревым.
Студенту следует ясно представлять себе физический смысл уравнений Максвелла (в интегральной форме), знать, что переменные электрическое и магнитное поля взаимосвязаны, они поддерживают друг друга и могут существовать независимо. Под энергией электромагнитного поля следует подразумевать сумму энергий электрического и магнитного полей.
Контрольная работа № 2 представлена набором таких задач, которые помогут студенту проверить свои знания по разделам «Электростатика», «Постоянный ток», «Электромагнетизм». Она включает в себя задачи на (Определение напряженности и разности потенциалов электрического поля, расчет простейших электрических полей с помощью принципа суперпозиции, определение электроемкости и энергии поля конденсаторов, применение законов Ома и Джоуля — Ленца.
Включены задачи на применение закона Био — Савара — Лапласа для расчета магнитной индукции (или напряженности) магнитного поля, создаваемого проводниками с током различной конфигурации, применение принципа суперпозиции при определении индукции или напряженности простейших полей, определение траектории движения заряженной частицы, ее удельного заряда и силы, действующей на движущуюся частицу в магнитном поле, вычисление работы, совершаемой силами как при движении прямолинейного проводника с током, так и при вращении контура с током различной конфигурации в магнитном поле, нахождение намагниченности, энергии и объемной плотности энергии магнитного поля соленоида и тороида.

Закон Кулона
ОСНОВНЫЕ ФОРМУЛЫ
F = ,
4Л£()£Г2 г
где (71 и — величины точечных зарядов,
Eq — электрическая постоянная,
е — диэлектрическая проницаемость среды,
г — расстояние между зарядами.
Напряженность электрического поля
Напряженность поля:
точечного заряда
бесконечно длинной заряженной нити
равномерно заряженной бесконечной плоскости
между двумя разноименно заряженными бесконечными плоскостями
e=f.
я
4tI£qE^
Т
2Я£ое/
а
2£ое’
Е=—
£q£
где т — линейная плотность заряда, ст — поверхностная заряда,
г — рсасстояние до поля.
Электрическое смещение
Работа перемещения заряда в электростатическом поле
плотность
источника
D — еоеЕ.
2
f £/а/=^(ф1-ф2),
где ф1 и ф2 — потенциалы начальной и конечной точек.

Ч
(Р=
4лЕо£Г
Потенциал поля точечного заряда

dtp
Связь между потенциалом и напряженностью
dl
Сила притяжения между двумя разноименно заряженными обкладками конденсатора
q2
2 2e&s’
где S' — площадь пластин.
Электроемкость:
уединенного проводника
плоского конденсатора
С=\
EoES
слоистого конденсатора
d ’
С= ,
аде,-
где d — расстояние между пластинами конденсатора,
dt — толщина ьго слоя диэлектрика,
е, — его диэлектрическая прони
цаемость.
Электроемкость батареи конденсато
ров, соединенных:
параллельно
С=ХС,;
последовательно
Энергия поля:
заряженного проводника
w =—=—=-■
заряженного конденсатора
3 2 2С 2 ’
W,=- еое£2Г, 2
V — объем конденсатора.
Объемная плотность энергии элект-
^Е2 D2 ED
И"э= =—=—
2 2£о6 2
z=d-f
dr
рического поля
Сила тока
Закон Ома:
в дифференциальной форме
• v Е j=yE=-;
в интегральной форме
р
где у — удельная проводимость, р — удельное сопротивление, U — напряжение на концах цепи,
R — сопротивление цепи, j — плотность тока.
Закон Джоуля — Ленца:
в дифференциальной форме
dn> у E2
—=]Е=уЕ2=—;
•
dr P
в интегральной форме
dQ=IUdt=^ dt=I2Rdt.
Сопротивление однородного проводника
где Z — длина проводника,
S — площадь его поперечного сечения.

р=ро(1+аО,
Зависимость удельного сопротивления от температуры
где а — температурный коэффициент сопротивления,

F=^E+^v хВ,
dF=/dlxB,
Pm = IS,
M=pwxB
^g/i°p/dlxr 4лг3
t — температура по шкале Цельсия.
Сила Лоренца
где v — скорость заряда q,
В — индукция магнитного поля.
Сила Ампера
где I — сила тока в проводнике, dl — элемент длины проводника.
Магнитный момент контура с током где S — площадь контура.
Механический момент, действующий на контур с током в магнитном поле Закон Бно-Савара-Лапласа
где д0 — магнитная постоянная,
д — магнитная проницаемость среды.
Магнитная индукция:

в=™±
2R
в=™±
2кг
(cosa1 +cosa2),
4кг
B=pQpnI,
в центре кругового тока
поля бесконечно длинного прямого тока
поля, созданного отрезком проводника с током
поля бесконечно длинного соленоида
где R — радиус кругового тока,
г — кратчайшее расстояние до оси проводника,
п — число витков на единицу длины соленоида,
ах и а2 — углы между отрезком проводника и линией, соединяющей концы отрезка с точкой поля.


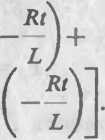
Сила взаимодействия двух прямолинейных бесконечно длинных параллельных токов на единицу их длины где г — расстояние между токами
4 и i2.
Работа по перемещению контура с током в магнитном поле
где Ф — магнитный поток через поверхность контура.
Магнитный поток однородного магнитного поля через площадку 5 где а — угол между вектором В и нормалью к площадке.
Закон электромагнитной индукции
где N — число витков контура.
Потокосцепление контура с током где L — индуктивность контура. Электродвижущая сила самоиндукции
Индуктивность соленоида
где V — объем соленоида п — число витков на единицу длины соленоида
Мгновенное значение силы тока в цепи, обладающей сопротивлением R и индуктивностью L
F=^T'
Ф=В5'соза,
, т d
- —N — =
dt dt
t = LL,
е^= —L-. dt
Z=Zoexp
1 — exp
Энергия магнитного поля
Объемная плотность энергии магнитного поля
_BH_ B2 -MH2
2 2pop 2
ПРИМЕРЫ PEI
HIM
ЯИЯ ЗАДАЧ
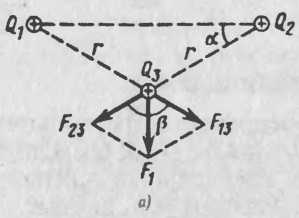
1. В углах при основании равнобедренного треугольника с боковой стороной 8 см расположены заряды и Q2- Определить силу, действующую на заряд 1нКл, помещенный в вершине треугольника. Угол при вершине 120°. Рассмотреть случаи:
а) С1 = Сг = 2 нКл;


Q1 02 fl=-—I’ 4Я££ог
2 10'9 Кл • 1 10
9 Кл
б)
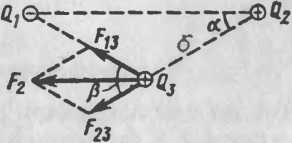
б) С1=-С2=2нКл.
Дано: 16,1=1621=2- 10“9 Кл; 6з=Ю’9 Кл; г=0,08 м; а=30°; £=1.
Найти: Fi; F2.
Решение. В соответствии с принципом суперпозиции поле каждого из зарядов 61 и Q2 действует на заряд 61 независимо. Это значит, что на заряд 6з действуют силы (рис. 1, а)
Fi3 = Qi ' Qt/C^nE^r2), F23 = Qi ' ОзК^пееоГ2).
Так как |Ci| = |£?2|, то ]F13| = |F23|. Векторная сумма F=F1+F2 является искомой величиной.Модульсилыопределяется по теореме косинусов F= Fi3+F23 + 2Fi3 ‘ F23 ‘ cos В случае одноименных зарядов 61 и Qz из рис. а видно, что угол /?=120°, поэтому Fi =F13=F23:
Рис. 1
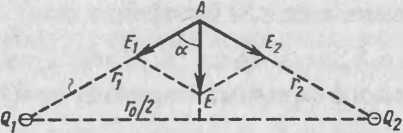 ность и потенциал поля в точке, расположенной на расстоянии 5 см от зарядов.
ность и потенциал поля в точке, расположенной на расстоянии 5 см от зарядов.
Дано: 2i = 62=-9*
• 10 9 Кл; е=81; го=0,08 м;
Г1=т2=0,05 м.
Найти: £, (р.
Решение. Напряженность ₽ис*2
поля, создаваемого в точке А (рис. 2) зарядами Qx и Q2 по принципу суперпозиции полей, равна векторной сумме напряженностей, создаваемых каждым из зарядов:

(1)
1 ... 4 5 6 7 8 9 10 11 12
ОСНОВНЫЕ ФОРМУЛЫ
F = ,
4Л£()£Г2 г
где (71 и — величины точечных зарядов,
Eq — электрическая постоянная,
е — диэлектрическая проницаемость среды,
г — расстояние между зарядами.
Напряженность электрического поля
Напряженность поля:
точечного заряда
бесконечно длинной заряженной нити
равномерно заряженной бесконечной плоскости
между двумя разноименно заряженными бесконечными плоскостями
e=f.
я
4tI£qE^
Т
2Я£ое/
а
2£ое’
Е=—
£q£
где т — линейная плотность заряда, ст — поверхностная заряда,
г — рсасстояние до поля.
Электрическое смещение
Работа перемещения заряда в электростатическом поле
плотность
источника
D — еоеЕ.
2
f £/а/=^(ф1-ф2),
где ф1 и ф2 — потенциалы начальной и конечной точек.

Ч
(Р=
4лЕо£Г
Потенциал поля точечного заряда

dtp
Связь между потенциалом и напряженностью
dl
Сила притяжения между двумя разноименно заряженными обкладками конденсатора
q2
2 2e&s’
где S' — площадь пластин.
Электроемкость:
уединенного проводника
плоского конденсатора
С=\
EoES
слоистого конденсатора
d ’
С= ,
аде,-
где d — расстояние между пластинами конденсатора,
dt — толщина ьго слоя диэлектрика,
е, — его диэлектрическая прони
цаемость.
Электроемкость батареи конденсато
ров, соединенных:
параллельно
С=ХС,;
последовательно
Энергия поля:
заряженного проводника
w =—=—=-■
заряженного конденсатора
3 2 2С 2 ’
W,=- еое£2Г, 2
V — объем конденсатора.
Объемная плотность энергии элект-
^Е2 D2 ED
И"э= =—=—
2 2£о6 2
z=d-f
dr
рического поля
Сила тока
Закон Ома:
в дифференциальной форме
• v Е j=yE=-;
в интегральной форме
р
где у — удельная проводимость, р — удельное сопротивление, U — напряжение на концах цепи,
R — сопротивление цепи, j — плотность тока.
Закон Джоуля — Ленца:
в дифференциальной форме
dn> у E2
—=]Е=уЕ2=—;
•
dr P
в интегральной форме
dQ=IUdt=^ dt=I2Rdt.
Сопротивление однородного проводника
где Z — длина проводника,
S — площадь его поперечного сечения.

р=ро(1+аО,
Зависимость удельного сопротивления от температуры
где а — температурный коэффициент сопротивления,

F=^E+^v хВ,
dF=/dlxB,
Pm = IS,
M=pwxB
^g/i°p/dlxr 4лг3
t — температура по шкале Цельсия.
Сила Лоренца
где v — скорость заряда q,
В — индукция магнитного поля.
Сила Ампера
где I — сила тока в проводнике, dl — элемент длины проводника.
Магнитный момент контура с током где S — площадь контура.
Механический момент, действующий на контур с током в магнитном поле Закон Бно-Савара-Лапласа
где д0 — магнитная постоянная,
д — магнитная проницаемость среды.
Магнитная индукция:

в=™±
2R
в=™±
2кг
(cosa1 +cosa2),
4кг
B=pQpnI,
в центре кругового тока
поля бесконечно длинного прямого тока
поля, созданного отрезком проводника с током
поля бесконечно длинного соленоида
где R — радиус кругового тока,
г — кратчайшее расстояние до оси проводника,
п — число витков на единицу длины соленоида,
ах и а2 — углы между отрезком проводника и линией, соединяющей концы отрезка с точкой поля.


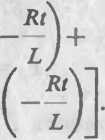
Сила взаимодействия двух прямолинейных бесконечно длинных параллельных токов на единицу их длины где г — расстояние между токами
4 и i2.
Работа по перемещению контура с током в магнитном поле
где Ф — магнитный поток через поверхность контура.
Магнитный поток однородного магнитного поля через площадку 5 где а — угол между вектором В и нормалью к площадке.
Закон электромагнитной индукции
где N — число витков контура.
Потокосцепление контура с током где L — индуктивность контура. Электродвижущая сила самоиндукции
Индуктивность соленоида
где V — объем соленоида п — число витков на единицу длины соленоида
Мгновенное значение силы тока в цепи, обладающей сопротивлением R и индуктивностью L
F=^T'
Ф=В5'соза,
, т d
- —N — =
dt dt
t = LL,
е^= —L-. dt
Z=Zoexp
1 — exp
Энергия магнитного поля
Объемная плотность энергии магнитного поля
_BH_ B2 -MH2
2 2pop 2
ПРИМЕРЫ PEI
HIM
ЯИЯ ЗАДАЧ
1. В углах при основании равнобедренного треугольника с боковой стороной 8 см расположены заряды и Q2- Определить силу, действующую на заряд 1нКл, помещенный в вершине треугольника. Угол при вершине 120°. Рассмотреть случаи:
а) С1 = Сг = 2 нКл;




Q1 02 fl=-—I’ 4Я££ог
2 10'9 Кл • 1 10
9 Клгде (71 и — величины точечных зарядов,
Eq — электрическая постоянная,
е — диэлектрическая проницаемость среды,
г — расстояние между зарядами.
Напряженность электрического поля
Напряженность поля:
точечного заряда
бесконечно длинной заряженной нити
равномерно заряженной бесконечной плоскости
между двумя разноименно заряженными бесконечными плоскостями
e=f.
я
4tI£qE^
Т
2Я£ое/
а
2£ое’
Е=—
£q£
где ф1 и ф2 — потенциалы начальной и конечной точек.

Ч
(Р=
4лЕо£Г
Потенциал поля точечного заряда

dtp
Связь между потенциалом и напряженностью
dl
Сила притяжения между двумя разноименно заряженными обкладками конденсатора
q2
2 2e&s’
где S' — площадь пластин.
Электроемкость:
уединенного проводника
плоского конденсатора
С=\
EoES
слоистого конденсатора
d ’
С= ,
аде,-
где d — расстояние между пластинами конденсатора,
dt — толщина ьго слоя диэлектрика,
е, — его диэлектрическая прони
цаемость.
Электроемкость батареи конденсато
ров, соединенных:
параллельно
С=ХС,;
последовательно
| Энергия поля: | |
| заряженного проводника | w =—=—=-■ |
| заряженного конденсатора | 3 2 2С 2 ’ W,=- еое£2Г, 2 |
| V — объем конденсатора. Объемная плотность энергии элект- | ^Е2 D2 ED И"э= =—=— 2 2£о6 2 z=d-f dr |
| рического поля Сила тока | |
| Закон Ома: в дифференциальной форме | • v Е j=yE=-; |
| в интегральной форме | р |
| где у — удельная проводимость, р — удельное сопротивление, U — напряжение на концах цепи, R — сопротивление цепи, j — плотность тока. Закон Джоуля — Ленца: в дифференциальной форме | dn> у E2 —=]Е=уЕ2=—; |
| • | dr P |
| в интегральной форме | dQ=IUdt=^ dt=I2Rdt. |
б)
б) С1=-С2=2нКл.
Дано: 16,1=1621=2- 10“9 Кл; 6з=Ю’9 Кл; г=0,08 м; а=30°; £=1.
Найти: Fi; F2.
Решение. В соответствии с принципом суперпозиции поле каждого из зарядов 61 и Q2 действует на заряд 61 независимо. Это значит, что на заряд 6з действуют силы (рис. 1, а)
Fi3 = Qi ' Qt/C^nE^r2), F23 = Qi ' ОзК^пееоГ2).
Так как |Ci| = |£?2|, то ]F13| = |F23|. Векторная сумма F=F1+F2 является искомой величиной.Модульсилыопределяется по теореме косинусов F= Fi3+F23 + 2Fi3 ‘ F23 ‘ cos В случае одноименных зарядов 61 и Qz из рис. а видно, что угол /?=120°, поэтому Fi =F13=F23:
Рис. 1
 ность и потенциал поля в точке, расположенной на расстоянии 5 см от зарядов.
ность и потенциал поля в точке, расположенной на расстоянии 5 см от зарядов.Дано: 2i = 62=-9*
• 10 9 Кл; е=81; го=0,08 м;
Г1=т2=0,05 м.
Найти: £, (р.
Решение. Напряженность ₽ис*2
поля, создаваемого в точке А (рис. 2) зарядами Qx и Q2 по принципу суперпозиции полей, равна векторной сумме напряженностей, создаваемых каждым из зарядов:

(1)
1 ... 4 5 6 7 8 9 10 11 12