ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 125
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Так же, как в предыдущем задании, наносим на числовую прямую параболы и заштриховываем искомые промежутки:
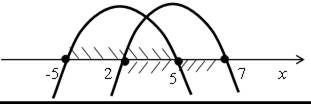
Получаем, что х [2; 5].
О т в е т: 2; 3; 4; 5.
Д о п о л н и т е л ь н ы е з а д а н и я.
1. № 379.
Р е ш е н и е
(а + 2) х2 + 8х + а – 4 = 0.
Чтобы данное уравнение имело 2 решения, необходимо выполнение следующих условий:
– уравнение должно быть квадратным, то есть а + 2 ≠ 0;
– дискриминант этого квадратного уравнения должен быть положителен.
Согласно этим условиям получим систему:
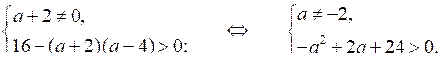
Решением второго неравенства системы является промежуток (–6; 4). С учетом того, что а ≠ –2, получим: а (–6; –2) (–2; 4).
О т в е т: (–6; –2) (–2; 4).
2. При каких значениях параметра а неравенство ах2 + 2ах + 4 > 0 выполняется на всей числовой оси?
Р е ш е н и е
Чтобы данное неравенство выполнялось на всей числовой оси, необходимо, чтобы ветви параболы были направлены вверх, и квадратный трехчлен не имел корней, то есть D1 = а2 – 4а < 0.
Решая это неравенство, получим, что а (0; 4). Этот промежуток удовлетворяет обоим условиям. Однако нужно рассмотреть еще случай, когда а = 0. Подставляя это значение в исходное неравенство, получим: 4 > 0.
Это неравенство верно, поэтому при а = 0 исходное неравенство будет выполняться на всей числовой оси.
О т в е т: [0; 4).
3. При каких значениях т область определения функции
f (х) = состоит из одной точки?
Р е ш е н и е
Чтобы найти область определения данной функции, нужно решить систему неравенств:
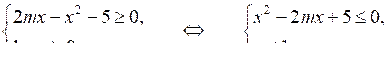
Эта система будет иметь единственное решение в двух случаях:
– если квадратный трехчлен х2 –2тх + 5 будет иметь единственный корень, не превосходящий 1:
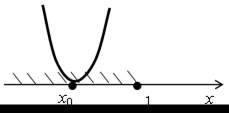
– если квадратный трехчлен х2 –2тх + 5 будет иметь два корня, меньший из которых равен 1:
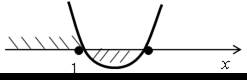
Первое условие будет выполнено, если дискриминант квадратного трехчлена х2 – 2тх + 5 равен нулю, а корень
х0 = ≤ 1. Имеем:
D1 = т2 – 5;
х0 = = m.
Получим систему:
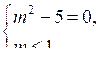
Ее решением является m = – .
Второе условие будет выполнено, если f (1) = 0, то есть 1 – 2т + 5 = 0, откуда т = 3. Подставляя это значение т, получим трехчлен х2 – 6х + 5; вторым его корнем будет число 5. Значит, т = 3 удовлетворяет условию задачи.
О т в е т: – ; 3.
V. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Опишите алгоритм решения неравенств второй степени с одной переменной.
– Когда решение неравенства второй степени с одной переменной будет состоять из единственного числа? из бесконечного множества чисел?
– Какие решения может иметь неравенство ах2 + bx + c > 0, если
а) а > 0 и х1, х2 – корни квадратного трехчлена ах2 + bx + c;
б) а < 0 и квадратный трехчлен имеет единственный корень х0;
в) а > 0 и квадратный трехчлен ах2 + bx + c не имеет корней?
Домашнее задание: № 311 (б), № 314 (б), № 319, № 320 (б, г, е).
Д о п о л н и т е л ь н о: № 321 (б), № 380.
У р о к 33 Дата:
РЕШЕНИЕ ЦЕЛЫХ РАЦИОНАЛЬНЫХ НЕРАВЕНСТВ
МЕТОДОМ ИНТЕРВАЛОВ
Цели: изучить метод интервалов; формировать умение его применять при решении целых рациональных неравенств.
Ход урока
I. Организационный момент.
II. Устная работа.
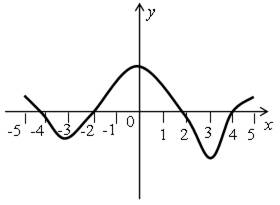
Назовите промежутки знакопостоянства функции у = f (х), если ее график изображен на рисунке.
III. Объяснение нового материала.
На этом уроке целесообразно изучить суть метода интервалов и рассмотреть его применение при решении целых рациональных неравенств. Как метод интервалов используются при решении дробно-рациональных неравенств лучше разобрать на следующем уроке.
Начать изучение новой темы лучше с постановки перед учащимися конкретной задачи: решить неравенство (х2 – 4) (х + 1) > 0. Это неравенство они должны решить, исходя из логических рассуждений, то есть отвечая на вопрос: когда произведение двух выражений положительно?
При ответе на этот вопрос возникают два случая: оба сомножителя одновременно положительны или одновременно отрицательны. Значит, нужно решить две системы неравенств:
1.
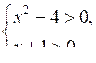2.
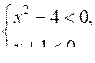
Решением первой системы будет промежуток (2; +∞), а решением второй – промежуток (–2; –1). Таким образом, получаем, что решением исходного неравенства будет объединение этих промежутков, то есть х (–2; –1) (2; +∞).
Исходя из результата, делается вывод, что такой способ решения неравенств подобного вида приемлем. Тогда учитель предлагает учащимся решить другое неравенство: (х2 – 4) (х + 1) (х – 7) > 0. Учащиеся осознают, что рассуждения о возможных знаках каждого из трех множителей будут громоздкими, поэтому лучше искать другой способ решения данного неравенства.
После этого следует разобрать суть метода интервалов и сделать вывод о том, что этот метод приемлем к целым неравенствам с любым количеством множителей, то есть он более универсален.
Затем можно вернуться к первому неравенству и решить его методом интервалов, разложив предварительно на множители выражение х2 – 4.
(х + 2) (х – 2) (х + 1) > 0;
х1 = –2, х2 = 2, х3 = –1.
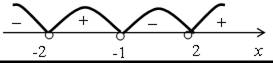
х (–2; –1) (2; +∞).
Необходимо обязательно добиться того, чтобы учащиеся осознали, что решение этого неравенства методом интервалов гораздо рациональнее.
Далее нужно рассмотреть случаи, когда до применения метода интервалов необходимо привести неравенство к стандартному виду:
(х – х1) (х – х2) … (х – хп) > < 0 (пример 2 и пример 3 из учебника).
IV. Формирование умений и навыков.
Упражнения:
1. № 325, № 327, № 328 (а).
2. Решите неравенство:
а) –(х – 3) (х + 5) > 0;
б) (4 – х) (х – 2) ≤ 0;
в) (2 + х)
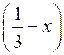> 0.В этой группе собраны неравенства, записанные не в том виде, к которому непосредственно применяется метод интервалов. Важно, чтобы у учащихся вырабатывался навык приведения неравенств к стандартному виду, иначе в дальнейшем могут возникать ошибки при расстановке знаков на интервалах.
V. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– На каком свойстве функции основан метод интервалов?
– Неравенства какого вида могут быть решены методом интервалов?
– В чем состоит метод интервалов решения неравенств?
Домашнее задание: № 326, № 328 (б), № 329.
У р о к 34 Дата:
РЕШЕНИЕ ЦЕЛЫХ И ДРОБНЫХ НЕРАВЕНСТВ
МЕТОДОМ ИНТЕРВАЛОВ
Цели: продолжить формирование умения решать целые неравенства методом интервалов; разобрать, как этим методом могут решаться дробные неравенства.
Ход урока
I. Организационный момент.
II. Устная работа.
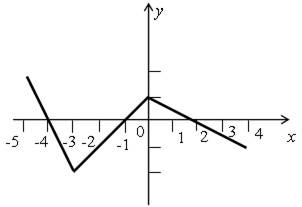
На рисунке изображен график функции у = f (х), определенной на отрезке [–5; 4]. Решите неравенство f (х) ≥ 0.
III. Проверочная работа.
В а р и а н т 1
Решите неравенство:
а) (х – 3) (х + 5) > 0; в) х
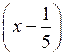(х + 2) > 0;б)
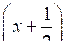(х – 1,7) ≤ 0; г) (х + 3) (х – 5) (1 – х) ≥ 0.В а р и а н т 2
Решите неравенство:
а) (х + 2) (х – 6) < 0; в) (х + 1) (х – 5)
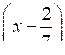< 0;б) (х + 0,3)
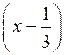≥ 0; г) х (4 – х) (1 + х) ≤ 0.IV. Формирование умений и навыков.
Все упражнения можно разбить на 2 группы. В первую группу войдут целые неравенства, которые учащиеся уже умеют решать. Во второй группе будут дробно-рациональные неравенства. Перед тем как приступать к их решению, необходимо объяснить учащимся особенности применения метода интервалов к неравенствам такого вида.
Упражнения:
1-я г р у п п а.