ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 1020
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
+ у)2 = 0;
х + у = 0;
х = –у.
Подставим найденное значение х во второе уравнение:
–у2 = –6;
у2 = 6;
у1 = х1 = – ;
у2 = – х2 = .
Заметим, что этот способ является более рациональным и интересным.
2-я г р у п п а.
1. № 451.
Р е ш е н и е
Известно, что прямая у = kx проходит через точку М (1; 2). Найдем значение k:
2 = k · 1 k = 2.
Таким образом, нужно найти точки пересечения графиков уравнений (х – 4)2 + (у – 6)2 = 25 и у = 2х. Для этого нужно решить систему:
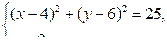
(х – 4)2 + (2х – 6)2 = 25;
х2 – 8х + 16 + 4х2 – 24х + 36 – 25 = 0;
5х2 – 32х + 27 = 0;
х1 = 1 у1 = 2 · 1 = 2;
х2 = 5,4 у2 = 2 · 5,4 = 10,8.
Ответ: (1; 2), (5,4; 10,8).
2. № 450.
Р е ш е н и е
Парабола у = х2 + 1 и прямая у = kx имеют только одну общую точку, если система имеет единственное решение.
Подставим значение у = kx в первое уравнение:
kx = х2 + 1;
х2 – kx + 1 = 0.
Составленная система будет иметь единственное решение, если это квадратное уравнение имеет один корень, то есть его дискриминант равен нулю.
D = k2 – 4;
k2 – 4 = 0;
k2 = 4;
k = ±2.
О т в е т: k = 2 и k = –2.
3. Решите систему уравнений:
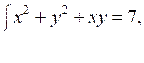
Р е ш е н и е
Сложим почленно правые и левые части уравнений системы. Получим:
х2 + у2 + 2ху + х + у = 12;
(х + у)2 + х + у = 12.
С д е л а е м з а м е н у: х + у = а – и решим полученное уравнение:
а2 + а – 12 = 0;
а1 = –4, а2 = 3.
В е р н е м с я к з а м е н е:
х + у = –4 х = –у – 4;
х + у = 3 х = 3 – у.
Подставляя поочередно данные выражения во второе уравнение исходной системы, получим:
О т в е т: (2; 1), (1; 2).
IV. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Что называется решением системы уравнений?
– Опишите способ подстановки решения систем уравнений второй степени.
– Опишите алгоритм решения систем уравнений второй степени способом сложения.
– Любое ли уравнение второй степени можно решить способом подстановки? способом сложения?
Домашнее задание: № 443 (б, г), № 446, № 447 (б).
Д о п о л н и т е л ь н о: № 438.
У р о к 46 Дата:
СУТЬ СПОСОБА РЕШЕНИЯ ЗАДАЧ
С ПОМОЩЬЮ СИСТЕМ УРАВНЕНИЙ
Цели: рассмотреть, как могут решаться текстовые задачи с помощью систем уравнений второй степени; формировать умение решать такие задачи.
Ход урока
I. Организационный момент.
II. Устная работа.
Решите систему уравнений:
а) б)
III. Объяснение нового материала.
Учащиеся уже умеют применять системы линейных уравнений для решения текстовых задач. Поэтому главным при изучении данного материала будет обобщение и систематизация их знаний о решении таких задач, а также закрепление методов решения систем уравнений второй степени.
Для демонстрации принципа решения задач с помощью систем уравнений второй степени достаточно привести пример из учебника.
IV. Формирование умений и навыков.
На этом уроке главное, чтобы учащиеся усвоили схему решения задач с помощью систем уравнений второй степени. Необходимо дать им под запись примерный план, согласно которому можно осуществлять решение таких задач.
1. Прочитать условие задачи и понять его.
2. Указать объекты, о которых идет речь в задаче.
3. Одну из величин обозначить за х, а другую – за у.
4. Составить систему уравнений по условию задачи.
5. Решить эту систему уравнений.
6. Интерпретировать полученные результаты.
На первых порах необходимо, чтобы учащиеся вслух комментировали решение задач согласно записанному плану.
Упражнения:
1. № 455, № 457.
2. № 460.
Покажем, как может быть решена эта задача по плану, приведенному выше.
Р е ш е н и е
1) В условии речь идет о прямоугольном треугольнике. Требуется найти его площадь.
2) Известна гипотенуза треугольника и его периметр. Для нахождения площади нужно знать его катеты.
3) Обозначим один катет треугольника через х см, а другой – через у см.
4) Зная периметр треугольника, составим уравнение:
х + у +37 = 84.
По теореме Пифагора составим второе уравнение:
х2 + у2 = 372.
Получим систему уравнений:
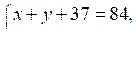
5) Решим эту систему уравнений способом подстановки:
472 – 94у + у2 + у2 – 372 = 0;
2у2 – 94у + (47 – 37) (47 + 37) = 0;
2у2 – 94у + 10 · 84 = 0;
у2 – 47у + 420 = 0;
у1 = 35 х1 = 12;
у2 = 12 х2 = 35.
6) Получаем, что катеты треугольника равны 12 см и 35 см. Найдем его площадь:
S = · 12 · 35 = 210 (см2).
О т в е т: 210 см2.
3. № 463.
При решении этой задачи учащимся поможет рисунок, сделанный согласно ее условию.
Пусть стороны прямоугольника равны х см и у см. Учитывая, что его площадь равна 30 см2, получим уравнение: ху = 30.
S1 = х2 см2, S2 = у2 см2.
Получим уравнение 2х2 + 2у2 = 122 или х2 + у2 = 61.
Составим систему уравнений:
Находим ее решения: (–6; –5), (6; 5), (–5; –6), (5; 6).
Первое и третье решения не подходят по условию задачи. Значит, стороны прямоугольника равны 5 см и 6 см.
О т в е т: 5 и 6 см.
V. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Какие существуют способы решения систем уравнений второй степени?
– В чем заключается каждый из этих способов?
– Опишите план решения текстовой задачи с помощью системы уравнений.
Домашнее задание: № 456, № 458, № 459.
У р о к 47 Дата:
РЕШЕНИЕ ЗАДАЧ НА ДВИЖЕНИЕ С ПОМОЩЬЮ
СИСТЕМ УРАВНЕНИЙ ВТОРОЙ СТЕПЕНИ
Цели: формировать умение решать задачи на движение с помощью систем уравнений второй степени.
Ход урока
I. Организационный момент.
II. Устная работа.
Периметр прямоугольника равен 20 см, а его площадь равна 21 см2. Пусть х и у – стороны этого прямоугольника. Какая из систем соответствует условию задачи?
а)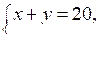 б)
б) 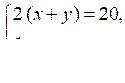 в)
в) 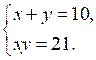
III. Проверочная работа.
В а р и а н т 1
1. Разность двух чисел равна 5, а их произведение равно 84. Найдите эти числа.
2. Прямоугольный участок земли площадью 2080 м2 обнесен изгородью, длина которой равна 184 м. Найдите длину и ширину участка.
В а р и а н т 2
1. Сумма двух чисел равна 25, а их произведение равно 144. Найдите эти числа.
2. Прямоугольный участок земли площадью 3250 м2 обнесен изгородью, длина которой равна 230 м. Найдите длину и ширину участка.
IV. Формирование умений и навыков.
Сначала необходимо актуализировать знания учащихся о решении задач на движение, выделив р я д э т а п о в.
1) Анализ условия:
– Какие объекты рассматриваются в задаче?
– Какое движение описано в задаче (однонаправленное, движение навстречу, по кругу и т. д.)?
– Значения каких величин известны?
2) Выделение процессов, которые описаны в задаче.
3) Выбор неизвестных величин и заполнение таблицы.
4) Составление системы уравнений.
5) Решение системы уравнений.
6) Интерпретация и проверка полученного решения.
Как реализуются описанные этапы, можно разобрать на примере задачи № 472.
Р е ш е н и е
1) В задаче описано движение двух пешеходов навстречу друг другу. Известно расстояние между пунктами и расстояние, которое прошли пешеходы за 4 часа.
2) Выделим два процесса:
– реальное движение пешеходов;
– движение при условии выхода одного из пешеходов на 1 ч раньше.
3) Пусть х км/ч – скорость первого пешехода и у км/ч – скорость второго пешехода.
Заполним две таблицы:
4) Известно, что расстояние от А до В равно 40 км, поэтому получим уравнение: 4х + 4у = 36. Известно, что при движении с заданным условием первый пешеход был в пути на 1 ч дольше, то есть получим уравнение: = 1.
Составим систему уравнений:
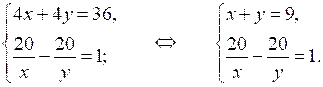
5) Решим ее способом подстановки:
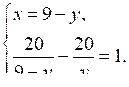
20у – 20 (9 – у) – у (9 – у) = 0;
20у – 180 + 20у – 9у + у2 = 0;
у2 + 31у – 180 = 0;
у1 = 5 х1 = 9 – 5 = 4;
у2 = – 36 (не подходит по смыслу задачи).
6) Получаем скорости пешеходов: 4 км/ч и 5 км/ч.
О т в е т: 4 и 5 км/ч.
Упражнения:
1. № 473, № 547.
2. № 461.
Р е ш е н и е
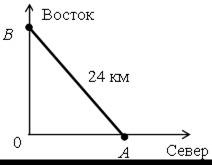
Пусть х км/ч – скорость первого отряда и у км/ч – скорость второго отряда.
Заполним таблицу:
х + у = 0;
х = –у.
Подставим найденное значение х во второе уравнение:
–у2 = –6;
у2 = 6;
у1 = х1 = – ;
у2 = – х2 = .
Заметим, что этот способ является более рациональным и интересным.
2-я г р у п п а.
1. № 451.
Р е ш е н и е
Известно, что прямая у = kx проходит через точку М (1; 2). Найдем значение k:
2 = k · 1 k = 2.
Таким образом, нужно найти точки пересечения графиков уравнений (х – 4)2 + (у – 6)2 = 25 и у = 2х. Для этого нужно решить систему:
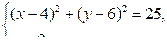
(х – 4)2 + (2х – 6)2 = 25;
х2 – 8х + 16 + 4х2 – 24х + 36 – 25 = 0;
5х2 – 32х + 27 = 0;
х1 = 1 у1 = 2 · 1 = 2;
х2 = 5,4 у2 = 2 · 5,4 = 10,8.
Ответ: (1; 2), (5,4; 10,8).
2. № 450.
Р е ш е н и е
Парабола у = х2 + 1 и прямая у = kx имеют только одну общую точку, если система имеет единственное решение.
Подставим значение у = kx в первое уравнение:
kx = х2 + 1;
х2 – kx + 1 = 0.
Составленная система будет иметь единственное решение, если это квадратное уравнение имеет один корень, то есть его дискриминант равен нулю.
D = k2 – 4;
k2 – 4 = 0;
k2 = 4;
k = ±2.
О т в е т: k = 2 и k = –2.
3. Решите систему уравнений:
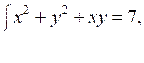
Р е ш е н и е
Сложим почленно правые и левые части уравнений системы. Получим:
х2 + у2 + 2ху + х + у = 12;
(х + у)2 + х + у = 12.
С д е л а е м з а м е н у: х + у = а – и решим полученное уравнение:
а2 + а – 12 = 0;
а1 = –4, а2 = 3.
В е р н е м с я к з а м е н е:
х + у = –4 х = –у – 4;
х + у = 3 х = 3 – у.
Подставляя поочередно данные выражения во второе уравнение исходной системы, получим:
| –у – 4 + у – у (у + 4) = 5; – 4 – у2 – 4у = 5; у2 + 4у + 9 = 0; D1 = 4 – 9 = –5. Нет решений. | 3 – у + у + у (3 – у) = 5; 3 + 3у – у2 = 5; у2 – 3у + 2 = 0; у1 = 1, у2 = 2. Тогда х1 = 3 – 1 = 2, х2 = 3 – 2 = 1. |
О т в е т: (2; 1), (1; 2).
IV. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Что называется решением системы уравнений?
– Опишите способ подстановки решения систем уравнений второй степени.
– Опишите алгоритм решения систем уравнений второй степени способом сложения.
– Любое ли уравнение второй степени можно решить способом подстановки? способом сложения?
Домашнее задание: № 443 (б, г), № 446, № 447 (б).
Д о п о л н и т е л ь н о: № 438.
У р о к 46 Дата:
СУТЬ СПОСОБА РЕШЕНИЯ ЗАДАЧ
С ПОМОЩЬЮ СИСТЕМ УРАВНЕНИЙ
Цели: рассмотреть, как могут решаться текстовые задачи с помощью систем уравнений второй степени; формировать умение решать такие задачи.
Ход урока
I. Организационный момент.
II. Устная работа.
Решите систему уравнений:
а) б)
III. Объяснение нового материала.
Учащиеся уже умеют применять системы линейных уравнений для решения текстовых задач. Поэтому главным при изучении данного материала будет обобщение и систематизация их знаний о решении таких задач, а также закрепление методов решения систем уравнений второй степени.
Для демонстрации принципа решения задач с помощью систем уравнений второй степени достаточно привести пример из учебника.
IV. Формирование умений и навыков.
На этом уроке главное, чтобы учащиеся усвоили схему решения задач с помощью систем уравнений второй степени. Необходимо дать им под запись примерный план, согласно которому можно осуществлять решение таких задач.
1. Прочитать условие задачи и понять его.
2. Указать объекты, о которых идет речь в задаче.
3. Одну из величин обозначить за х, а другую – за у.
4. Составить систему уравнений по условию задачи.
5. Решить эту систему уравнений.
6. Интерпретировать полученные результаты.
На первых порах необходимо, чтобы учащиеся вслух комментировали решение задач согласно записанному плану.
Упражнения:
1. № 455, № 457.
2. № 460.
Покажем, как может быть решена эта задача по плану, приведенному выше.
Р е ш е н и е
1) В условии речь идет о прямоугольном треугольнике. Требуется найти его площадь.
2) Известна гипотенуза треугольника и его периметр. Для нахождения площади нужно знать его катеты.
3) Обозначим один катет треугольника через х см, а другой – через у см.
4) Зная периметр треугольника, составим уравнение:
х + у +37 = 84.
По теореме Пифагора составим второе уравнение:
х2 + у2 = 372.
Получим систему уравнений:
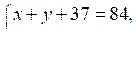
5) Решим эту систему уравнений способом подстановки:
472 – 94у + у2 + у2 – 372 = 0;
2у2 – 94у + (47 – 37) (47 + 37) = 0;
2у2 – 94у + 10 · 84 = 0;
у2 – 47у + 420 = 0;
у1 = 35 х1 = 12;
у2 = 12 х2 = 35.
6) Получаем, что катеты треугольника равны 12 см и 35 см. Найдем его площадь:
S = · 12 · 35 = 210 (см2).
О т в е т: 210 см2.
3. № 463.
При решении этой задачи учащимся поможет рисунок, сделанный согласно ее условию.
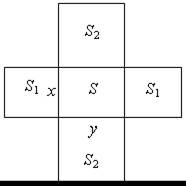 | S = 30 см2 2S1 + 2S2 = 122 см2 |
Пусть стороны прямоугольника равны х см и у см. Учитывая, что его площадь равна 30 см2, получим уравнение: ху = 30.
S1 = х2 см2, S2 = у2 см2.
Получим уравнение 2х2 + 2у2 = 122 или х2 + у2 = 61.
Составим систему уравнений:
Находим ее решения: (–6; –5), (6; 5), (–5; –6), (5; 6).
Первое и третье решения не подходят по условию задачи. Значит, стороны прямоугольника равны 5 см и 6 см.
О т в е т: 5 и 6 см.
V. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Какие существуют способы решения систем уравнений второй степени?
– В чем заключается каждый из этих способов?
– Опишите план решения текстовой задачи с помощью системы уравнений.
Домашнее задание: № 456, № 458, № 459.
У р о к 47 Дата:
РЕШЕНИЕ ЗАДАЧ НА ДВИЖЕНИЕ С ПОМОЩЬЮ
СИСТЕМ УРАВНЕНИЙ ВТОРОЙ СТЕПЕНИ
Цели: формировать умение решать задачи на движение с помощью систем уравнений второй степени.
Ход урока
I. Организационный момент.
II. Устная работа.
Периметр прямоугольника равен 20 см, а его площадь равна 21 см2. Пусть х и у – стороны этого прямоугольника. Какая из систем соответствует условию задачи?
а)
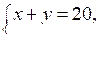 б)
б) 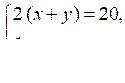 в)
в) 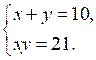
III. Проверочная работа.
В а р и а н т 1
1. Разность двух чисел равна 5, а их произведение равно 84. Найдите эти числа.
2. Прямоугольный участок земли площадью 2080 м2 обнесен изгородью, длина которой равна 184 м. Найдите длину и ширину участка.
В а р и а н т 2
1. Сумма двух чисел равна 25, а их произведение равно 144. Найдите эти числа.
2. Прямоугольный участок земли площадью 3250 м2 обнесен изгородью, длина которой равна 230 м. Найдите длину и ширину участка.
IV. Формирование умений и навыков.
Сначала необходимо актуализировать знания учащихся о решении задач на движение, выделив р я д э т а п о в.
1) Анализ условия:
– Какие объекты рассматриваются в задаче?
– Какое движение описано в задаче (однонаправленное, движение навстречу, по кругу и т. д.)?
– Значения каких величин известны?
2) Выделение процессов, которые описаны в задаче.
3) Выбор неизвестных величин и заполнение таблицы.
4) Составление системы уравнений.
5) Решение системы уравнений.
6) Интерпретация и проверка полученного решения.
Как реализуются описанные этапы, можно разобрать на примере задачи № 472.
Р е ш е н и е
1) В задаче описано движение двух пешеходов навстречу друг другу. Известно расстояние между пунктами и расстояние, которое прошли пешеходы за 4 часа.
2) Выделим два процесса:
– реальное движение пешеходов;
– движение при условии выхода одного из пешеходов на 1 ч раньше.
3) Пусть х км/ч – скорость первого пешехода и у км/ч – скорость второго пешехода.
Заполним две таблицы:
| Реальное движение пешеходов | | Движение с заданным условием | ||||||
| | S | V | t | | S | V | t | |
| 1-й | 4х км | х км/ч | 4 ч | 1-й | 20 км | х км/ч | ч | |
| 2-й | 4у км | у км/ч | 4 ч | 2-й | 20 км | у км/ч | ч | |
4) Известно, что расстояние от А до В равно 40 км, поэтому получим уравнение: 4х + 4у = 36. Известно, что при движении с заданным условием первый пешеход был в пути на 1 ч дольше, то есть получим уравнение: = 1.
Составим систему уравнений:
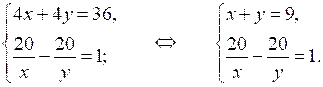
5) Решим ее способом подстановки:
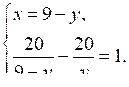
20у – 20 (9 – у) – у (9 – у) = 0;
20у – 180 + 20у – 9у + у2 = 0;
у2 + 31у – 180 = 0;
у1 = 5 х1 = 9 – 5 = 4;
у2 = – 36 (не подходит по смыслу задачи).
6) Получаем скорости пешеходов: 4 км/ч и 5 км/ч.
О т в е т: 4 и 5 км/ч.
Упражнения:
1. № 473, № 547.
2. № 461.
Р е ш е н и е

Пусть х км/ч – скорость первого отряда и у км/ч – скорость второго отряда.
Заполним таблицу:
| | S | V | t |
| 1-й отряд | 4х км | х км/ч | 4 ч |
| 2-й отряд | 4у км | у км/ч | 4 ч |