Файл: Методические указания к лабораторным работам для студентов специальности 140101.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.10.2023
Просмотров: 159
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
rкр;
– сравнивают найденное значение rкр с полученным ri. При
ri > rкр результат хi признается грубым промахом и исключается из совокупности. Далее обработка результатов возвращается к п.2. При ri rкр переходят к п. 4.
– задается величина уровня значимости для доверительного интервала ;
– по числу степеней свободы ν = n - l и принятому из табл.
П 2.2. находят значение параметра tкр;
– по (3.8) рассчитывается величина вероятного отклонения ;
– по (3.5) рассчитывается доверительный интервал значения mx.
Задание на лабораторную работу
Для указанного преподавателем варианта исходных данных в табл. П 1.1 выполнить:
Вычисления произвести для уровня значимости = 0,05 и 0,01.
Пример выполнения лабораторной работы
Предположим, что в результате восьми параллельных измерений случайная величина Х приняла следующие значения:
Запишем в ячейку А1 заголовок Лабораторная работа №3, а в ячейки А3, В3, C3 и D3 заголовки таблицы исходных данных №, х, dи r. Далее пронумеруем ячейки А4:А11 от 1 до 8, а в ячейки В4:В11 занесем значения случайной величины. В ячейках А13:А15 укажем заголовки рассчитываемых величин хср, S2и S. Активизируем ячейку В13 и вычислим среднее арифметическое с помощью функции СРЗНАЧ из категории Статистические. Затем в ячейках В14 и В15 вычислим дисперсию с помощью функции ДИСПи среднеквадратичное отклонение с помощью функции СТАНДОТКЛОН.
Активизируем ячейку С4 и в ней вычисляем отклонение значения случайной величины от среднего, записав формулу =ABS(B4-$B$13). Затем растягиваем эту ячейку до С11.
В массиве С4:С11 наибольшее отклонение 0,1425 имеет величина х5=1,54. Для нее в ячейке D8 рассчитываем значение критерия r, записав формулу =C8/B15/КОРЕНЬ((8-1)/8). В ячейках С13 и С14 указываем заголовки табличных значений критерия rкр для уровней значимости α = 0,05 и 0,01, а в ячейках D13 и D14 – значения критериев, взятые из табл. П 2.1, соответственно 2,172 и 2,374.
Сравнивая полученное в ячейке D8 значение критерия r= 2,298 с табличными, делаем вывод, что с вероятностью ошибки α = 0,05 значение х5=1,54 следует признать грубым промахом и исключить из совокупности. Если снизить вероятность ошибки до α = 0,01, то рассчитанное по (3.9) значение критерия 2,298 будет меньше табличного значения 2,374, поэтому следует оставить это значение в совокупности для расчета доверительного интервала.
Для уровня значимости α = 0,05 формируем новую совокупность исходных данных из семи значений случайной величины. В ячейках F4:F10 указываем номера значений, в ячейках G4:G10 – сами значения, далее, как и в предыдущем случае, рассчитываем среднее арифметическое, дисперсию и среднеквадратичное отклонение. В ячейках Н4:Н10 вычисляем отклонения случайных величин от среднего.
Для новой совокупности наибольшее отклонение d= 0,0529 имеет случайная величина х2= 1,43. Для нее значение критерия r, рассчитанное по (3.9), составляет 1,610. Для уровня значимости α = 0,05 и числа степеней свободы ν = 5 табличное значение критерия rкр=2,093. Так как
r < rкр, то следует признать, что наблюдаемое отклонение вероятнее всего вызвано случайными факторами, и оставить х2 в совокупности исходных данных.
Для расчета доверительного интервала с уровнем значимости
α = 0,01 используется совокупность из восьми значений со средним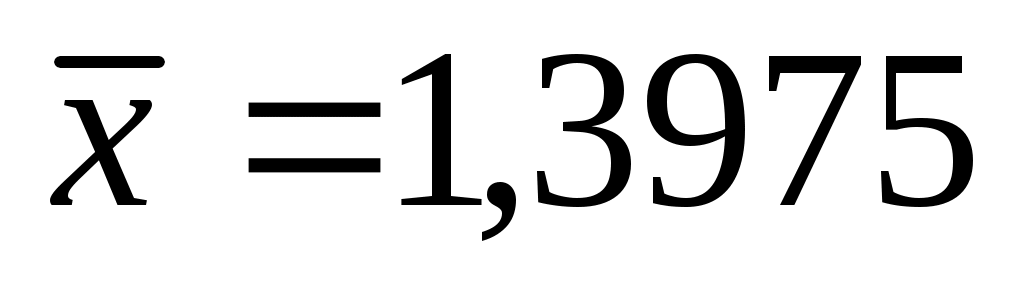
. В ячейке В20 вычислим коэффициент вариации, используя формулу =B15/B13*100. В ячейку В21 введем значение критерия Стьюдента tкр=3,4995, выбрав его из табл. П 2.2 или используя функцию EXCEL =СТЬЮДРАСПОБР(0,01;7) по уровню значимости
α = 0,01 и числу степеней свободы ν = 8 - 1 = 7. В ячейке В22 по (3.8) вычислим отклонение границы интервала от среднего значения, введя формулу =B21*B15/КОРЕНЬ(8). Затем в ячейки А23:А25 запишем заголовки значений границ и середины доверительного интервала, скопируем в ячейку В24 содержимое ячейки В13, а нижнюю и верхнюю границы интервала вычислим с помощью формул =B13-B22 и =B13+B22.
Для уровня значимости α = 0,05 проведем аналогичные расчеты, используя массив данных G4:G10 из семи случайных величин со средним арифметическим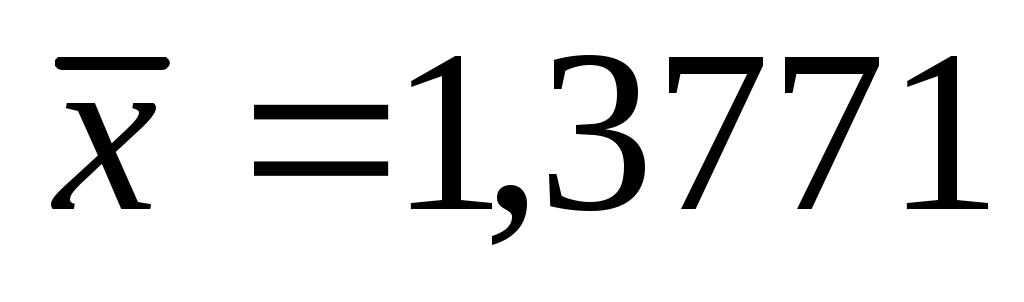
и критерием Стьюдента tкр=2,4469, взятым для α = 0,05 и ν = 6. Результаты вычислений занесем в ячейки G20:G25.
Нанесем границы доверительных интервалов на график. Подпрограмма Мастер диаграмм позволяет строить двух- и трехмерные графики. Для того чтобы построить одномерный график, т.е. нанести на числовую ось значения случайной величины, зададим для всех значений координаты по оси ординат равными нулю. Для уровня значимости α = 0,01 в ячейках С23:С25 введем нулевые значения, выделим массив В23:С25 и вызовем Мастер диаграмм.
В открывшемся меню выберем тип диаграммы Точечная, далее выберем диаграмму с линиями и маркерами и нажмем кнопку Готово. Переместим открывшуюся диаграмму и проведем ее форматирование:
1) выделим и удалим Легенду «Ряд1»;
2) щелкнем мышкой по области построения диаграммы, выберем пункт Формат области построения и в нем сделаем рамку невидимой, а заливку прозрачной;
3) щелкнем мышкой по области диаграммы, выберем пункт Формат области диаграммыи в нем сделаем рамку невидимой;
4) щелкнем мышкой по области диаграммы, выберем пункт Параметры диаграммы; в меню Заголовки в строке Название диаграммызапишем Доверительный интервал для уровня значимости 0,01; в строке Ось х укажем обозначение случайной величины
х; в меню Оси снимем флажок с оси у; в меню Линии сетки для оси у снимем флажок с пункта Основные линии;
5) щелкнем мышкой по оси х, выберем пункт Формат оси и в нем укажем минимальное и максимальное значения шкалы, цену основных делений, тип и размер шрифта;
6) щелкнем поочередно по надписи и заголвку оси и выберем тип и размер шрифта.
Для уровня значимости α = 0,05 выполним аналогичные операции. Вид рабочего листа для лабораторной работы №3 показан на рис.3.1.
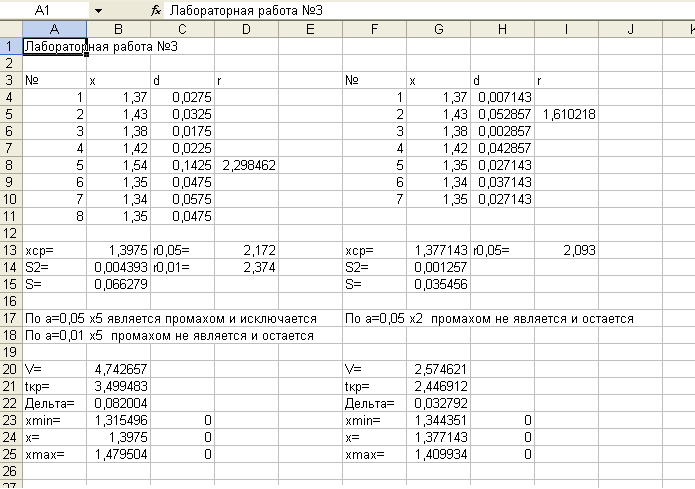
Рис. 3.1. Вид рабочего листа лабораторной работы №3
Лабораторная работа №4
Сравнение двух средних величин и оценка
однородности дисперсии результатов измерений
При измерении одних и тех же величин различными способами или в различные периоды времени результаты, как правило, несколько отличаются друг от друга. Если исходить из того, что каждый результат может быть отягощен некоторой ошибкой, абсолютная величина и знак которой неизвестны, то при сопоставлении результатов возникает неопределенность в оценке: соответствует ли имеющееся между ними различие различию между измеряемыми параметрами или мы наблюдаем две реализации одной случайной величины, а видимое различие связано только лишь со случайными колебаниями неконтролируемых параметров. Эта неопределенность проясняется при решении двух взаимосвязанных вопросов.
1) Значимо ли различается воспроизводимость результатов (равноточны ли измерения) в разных сериях опытов?
Вопрос о равноточности двух серий измерений решается путем сопоставления дисперсий результатов измерений в этих сериях. Мерой оценки статистически значимого различия дисперсий является критерий Фишера:
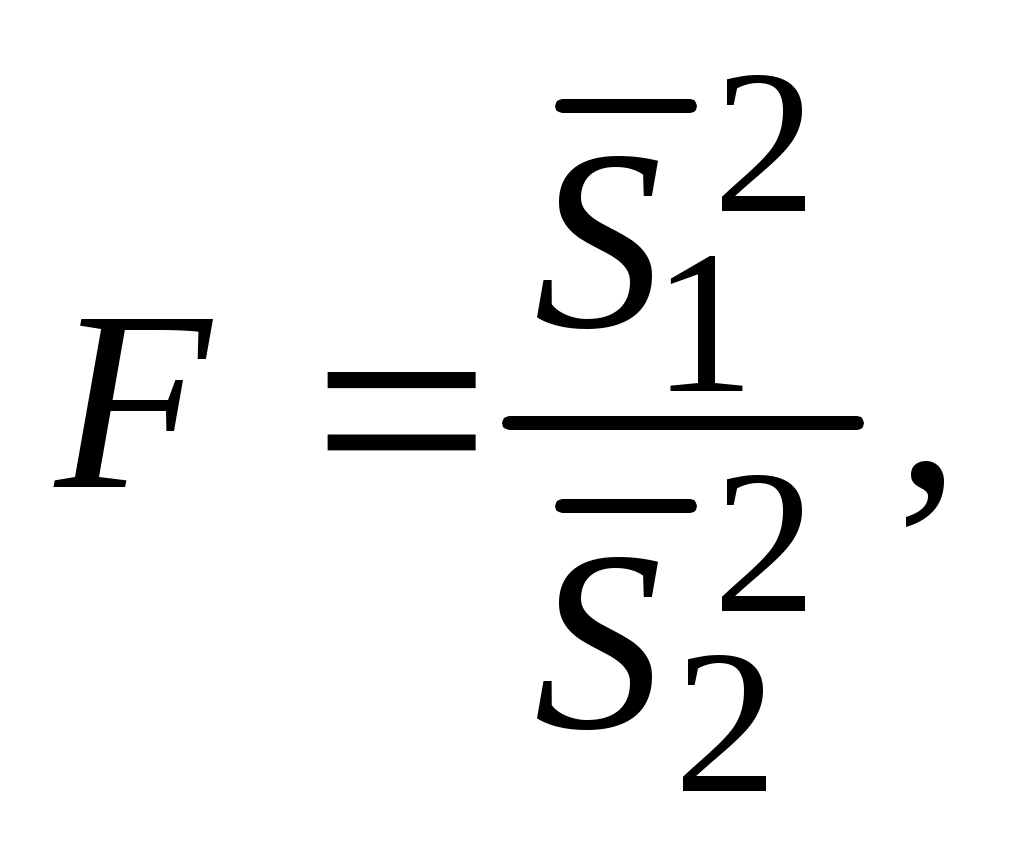(4.1)
где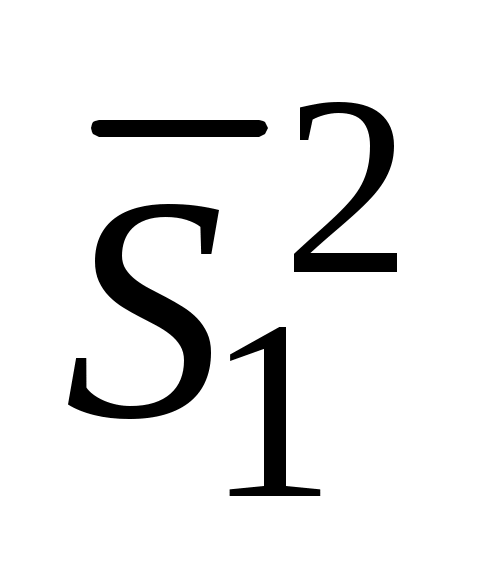
– наибольшая дисперсия, > 
.
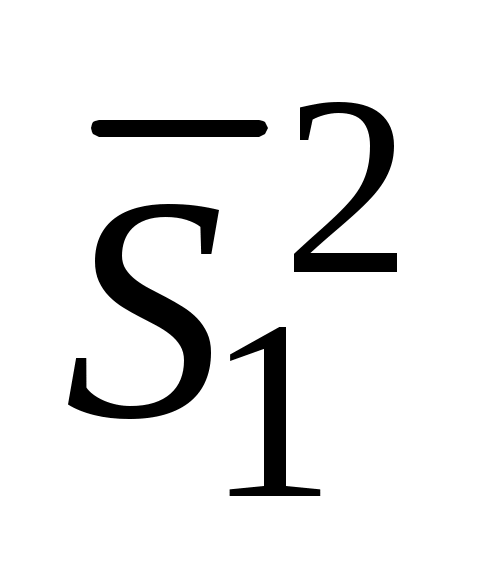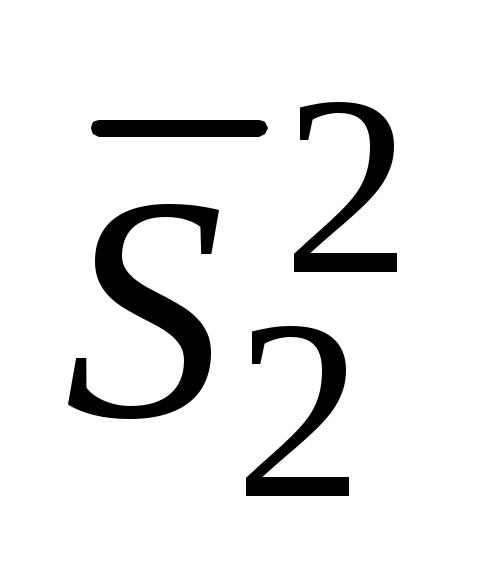Найденное по (4.1) значение критерия F сравнивают с критическим Fкр (
, ν1 ν2), значения которого для различных уровней значимости и степеней свободы ν1 = n1 - 1 и ν2 = n2 - 1 приведены в табл.
П 2.3. Здесь n1 и n2 – количество параллельных измерений в сериях опытов соответственно с результатами, имеющими наибольшую и наименьшую дисперсии.
При F > Fкр с доверительной вероятностью β = 1 – можно считать, что дисперсии в первой и второй сериях опытов статистически неодинаковы, воспроизводимость результатов во второй серии опытов выше (в этой серии были выполнены более точные измерения). При
F < Fкр на основании данных измерений можно считать, что точность измерений в обеих сериях опытов приблизительно одинакова.
Риск ошибки в признании двух дисперсий статистически неравными при F > Fкр составляет величину только в том случае, если есть основание полагать, что в одной серии опытов разброс результатов относительно среднего должен быть меньше, в частности за счет применения более совершенных приборов или более сложных методик измерения. Если этого заранее утверждать нельзя, то необходимо пользоваться двухсторонними доверительными границами, предполагая, что разброс данных (величина дисперсии) в одной серии опытов может быть как больше, так и меньше, чем в другой серии. Используя для сравнения дисперсий значения Fкр из табл. П 2.3 для уровня значимости , получим риск ошибки 2.
Если дисперсии двух серий опытов не отличаются значимо друг от друга, то определить, есть ли статистически значимая разница в результатах серий, можно с помощью t-распределения Стьюдента. Для этого вычисляют среднее взвешенное двух дисперсий:
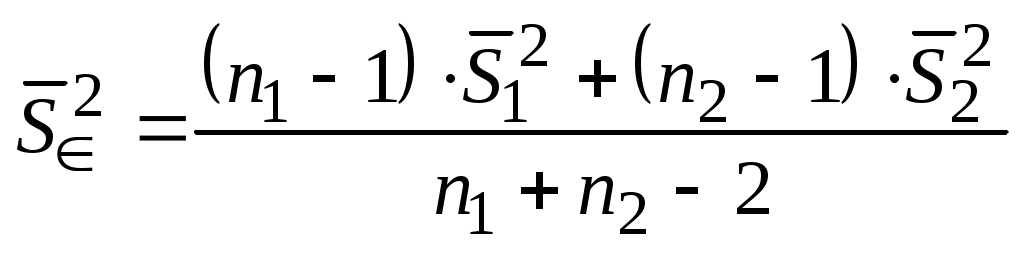(4.2)
и величину:
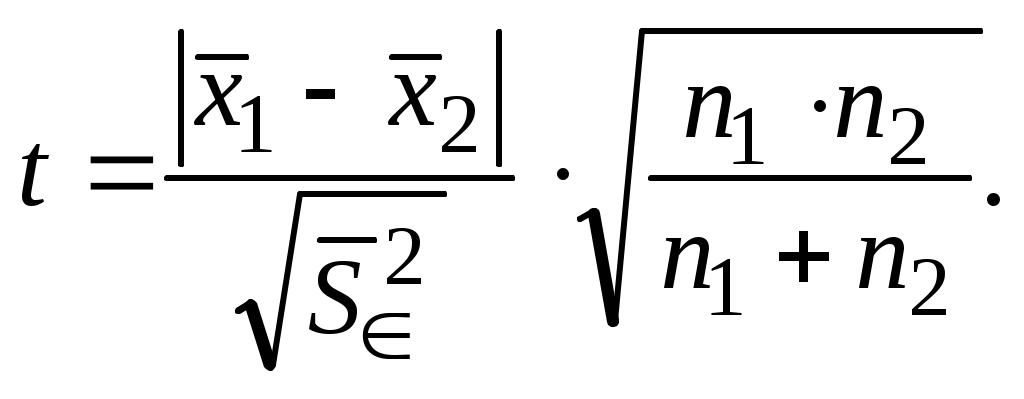(4.3)
Далее для числа степеней свободы ν= n1 + n2 - 2 и уровня значимости из табл. П 2.2 или с помощью функции EXCEL СТЬЮДРАСПОБР определяют критическое значение tкр. Если t < tкр, то принимают, что
и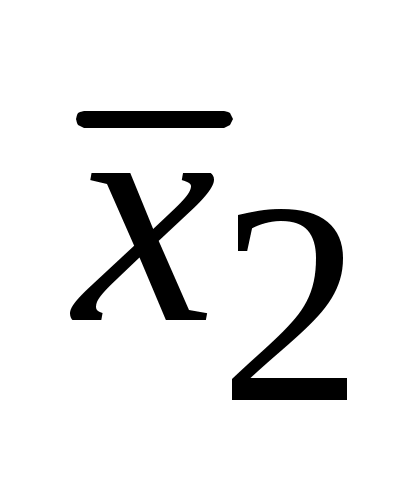 
являются оценками одного математического ожидания
– сравнивают найденное значение rкр с полученным ri. При
ri > rкр результат хi признается грубым промахом и исключается из совокупности. Далее обработка результатов возвращается к п.2. При ri rкр переходят к п. 4.
-
По (3.4) вычисляется коэффициент вариации V. -
Вычисляется доверительный интервал значения mx, для чего:
– задается величина уровня значимости для доверительного интервала ;
– по числу степеней свободы ν = n - l и принятому из табл.
П 2.2. находят значение параметра tкр;
– по (3.8) рассчитывается величина вероятного отклонения ;
– по (3.5) рассчитывается доверительный интервал значения mx.
Задание на лабораторную работу
Для указанного преподавателем варианта исходных данных в табл. П 1.1 выполнить:
-
для всей совокупности исходных данных (n = 12) проверить наличие грубых промахов и при обнаружении исключить из совокупности; -
для оставшихся в совокупности значений рассчитать их среднее арифметическое, дисперсию, среднеквадратичное отклонение, коэффициент вариации, доверительный интервал; -
нанести на числовую ось в масштабе среднее значение и границы доверительного интервала.
Вычисления произвести для уровня значимости = 0,05 и 0,01.
Пример выполнения лабораторной работы
Предположим, что в результате восьми параллельных измерений случайная величина Х приняла следующие значения:
-
№
1
2
3
4
5
6
7
8
Х
1,37
1,43
1,38
1,42
1,54
1,35
1,34
1,35
Запишем в ячейку А1 заголовок Лабораторная работа №3, а в ячейки А3, В3, C3 и D3 заголовки таблицы исходных данных №, х, dи r. Далее пронумеруем ячейки А4:А11 от 1 до 8, а в ячейки В4:В11 занесем значения случайной величины. В ячейках А13:А15 укажем заголовки рассчитываемых величин хср, S2и S. Активизируем ячейку В13 и вычислим среднее арифметическое с помощью функции СРЗНАЧ из категории Статистические. Затем в ячейках В14 и В15 вычислим дисперсию с помощью функции ДИСПи среднеквадратичное отклонение с помощью функции СТАНДОТКЛОН.
Активизируем ячейку С4 и в ней вычисляем отклонение значения случайной величины от среднего, записав формулу =ABS(B4-$B$13). Затем растягиваем эту ячейку до С11.
В массиве С4:С11 наибольшее отклонение 0,1425 имеет величина х5=1,54. Для нее в ячейке D8 рассчитываем значение критерия r, записав формулу =C8/B15/КОРЕНЬ((8-1)/8). В ячейках С13 и С14 указываем заголовки табличных значений критерия rкр для уровней значимости α = 0,05 и 0,01, а в ячейках D13 и D14 – значения критериев, взятые из табл. П 2.1, соответственно 2,172 и 2,374.
Сравнивая полученное в ячейке D8 значение критерия r= 2,298 с табличными, делаем вывод, что с вероятностью ошибки α = 0,05 значение х5=1,54 следует признать грубым промахом и исключить из совокупности. Если снизить вероятность ошибки до α = 0,01, то рассчитанное по (3.9) значение критерия 2,298 будет меньше табличного значения 2,374, поэтому следует оставить это значение в совокупности для расчета доверительного интервала.
Для уровня значимости α = 0,05 формируем новую совокупность исходных данных из семи значений случайной величины. В ячейках F4:F10 указываем номера значений, в ячейках G4:G10 – сами значения, далее, как и в предыдущем случае, рассчитываем среднее арифметическое, дисперсию и среднеквадратичное отклонение. В ячейках Н4:Н10 вычисляем отклонения случайных величин от среднего.
Для новой совокупности наибольшее отклонение d= 0,0529 имеет случайная величина х2= 1,43. Для нее значение критерия r, рассчитанное по (3.9), составляет 1,610. Для уровня значимости α = 0,05 и числа степеней свободы ν = 5 табличное значение критерия rкр=2,093. Так как
r < rкр, то следует признать, что наблюдаемое отклонение вероятнее всего вызвано случайными факторами, и оставить х2 в совокупности исходных данных.
Для расчета доверительного интервала с уровнем значимости
α = 0,01 используется совокупность из восьми значений со средним
. В ячейке В20 вычислим коэффициент вариации, используя формулу =B15/B13*100. В ячейку В21 введем значение критерия Стьюдента tкр=3,4995, выбрав его из табл. П 2.2 или используя функцию EXCEL =СТЬЮДРАСПОБР(0,01;7) по уровню значимости α = 0,01 и числу степеней свободы ν = 8 - 1 = 7. В ячейке В22 по (3.8) вычислим отклонение границы интервала от среднего значения, введя формулу =B21*B15/КОРЕНЬ(8). Затем в ячейки А23:А25 запишем заголовки значений границ и середины доверительного интервала, скопируем в ячейку В24 содержимое ячейки В13, а нижнюю и верхнюю границы интервала вычислим с помощью формул =B13-B22 и =B13+B22.
Для уровня значимости α = 0,05 проведем аналогичные расчеты, используя массив данных G4:G10 из семи случайных величин со средним арифметическим
и критерием Стьюдента tкр=2,4469, взятым для α = 0,05 и ν = 6. Результаты вычислений занесем в ячейки G20:G25. Нанесем границы доверительных интервалов на график. Подпрограмма Мастер диаграмм позволяет строить двух- и трехмерные графики. Для того чтобы построить одномерный график, т.е. нанести на числовую ось значения случайной величины, зададим для всех значений координаты по оси ординат равными нулю. Для уровня значимости α = 0,01 в ячейках С23:С25 введем нулевые значения, выделим массив В23:С25 и вызовем Мастер диаграмм.
В открывшемся меню выберем тип диаграммы Точечная, далее выберем диаграмму с линиями и маркерами и нажмем кнопку Готово. Переместим открывшуюся диаграмму и проведем ее форматирование:
1) выделим и удалим Легенду «Ряд1»;
2) щелкнем мышкой по области построения диаграммы, выберем пункт Формат области построения и в нем сделаем рамку невидимой, а заливку прозрачной;
3) щелкнем мышкой по области диаграммы, выберем пункт Формат области диаграммыи в нем сделаем рамку невидимой;
4) щелкнем мышкой по области диаграммы, выберем пункт Параметры диаграммы; в меню Заголовки в строке Название диаграммызапишем Доверительный интервал для уровня значимости 0,01; в строке Ось х укажем обозначение случайной величины
х; в меню Оси снимем флажок с оси у; в меню Линии сетки для оси у снимем флажок с пункта Основные линии;
5) щелкнем мышкой по оси х, выберем пункт Формат оси и в нем укажем минимальное и максимальное значения шкалы, цену основных делений, тип и размер шрифта;
6) щелкнем поочередно по надписи и заголвку оси и выберем тип и размер шрифта.
Для уровня значимости α = 0,05 выполним аналогичные операции. Вид рабочего листа для лабораторной работы №3 показан на рис.3.1.
Рис. 3.1. Вид рабочего листа лабораторной работы №3
Лабораторная работа №4
Сравнение двух средних величин и оценка
однородности дисперсии результатов измерений
При измерении одних и тех же величин различными способами или в различные периоды времени результаты, как правило, несколько отличаются друг от друга. Если исходить из того, что каждый результат может быть отягощен некоторой ошибкой, абсолютная величина и знак которой неизвестны, то при сопоставлении результатов возникает неопределенность в оценке: соответствует ли имеющееся между ними различие различию между измеряемыми параметрами или мы наблюдаем две реализации одной случайной величины, а видимое различие связано только лишь со случайными колебаниями неконтролируемых параметров. Эта неопределенность проясняется при решении двух взаимосвязанных вопросов.
1) Значимо ли различается воспроизводимость результатов (равноточны ли измерения) в разных сериях опытов?
-
Значимо ли различаются средние значения результатов в сериях?
Вопрос о равноточности двух серий измерений решается путем сопоставления дисперсий результатов измерений в этих сериях. Мерой оценки статистически значимого различия дисперсий является критерий Фишера:
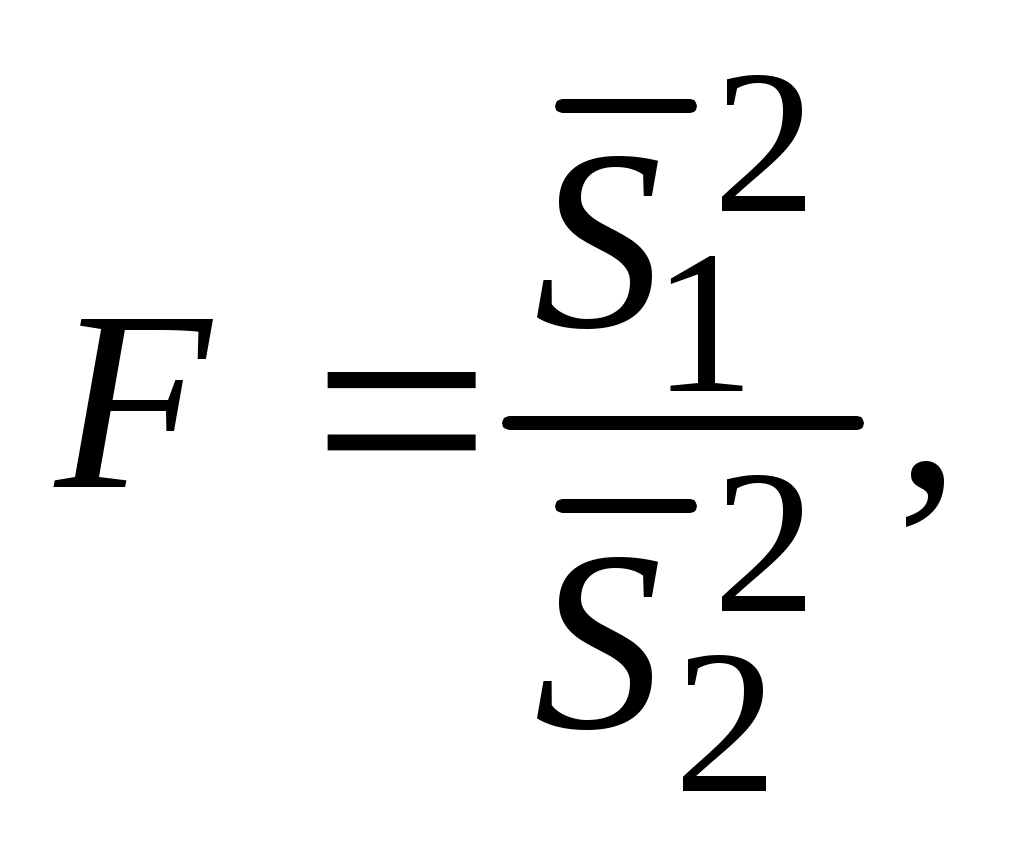(4.1)где
– наибольшая дисперсия, > .Найденное по (4.1) значение критерия F сравнивают с критическим Fкр (
, ν1 ν2), значения которого для различных уровней значимости и степеней свободы ν1 = n1 - 1 и ν2 = n2 - 1 приведены в табл.
П 2.3. Здесь n1 и n2 – количество параллельных измерений в сериях опытов соответственно с результатами, имеющими наибольшую и наименьшую дисперсии.
При F > Fкр с доверительной вероятностью β = 1 – можно считать, что дисперсии в первой и второй сериях опытов статистически неодинаковы, воспроизводимость результатов во второй серии опытов выше (в этой серии были выполнены более точные измерения). При
F < Fкр на основании данных измерений можно считать, что точность измерений в обеих сериях опытов приблизительно одинакова.
Риск ошибки в признании двух дисперсий статистически неравными при F > Fкр составляет величину только в том случае, если есть основание полагать, что в одной серии опытов разброс результатов относительно среднего должен быть меньше, в частности за счет применения более совершенных приборов или более сложных методик измерения. Если этого заранее утверждать нельзя, то необходимо пользоваться двухсторонними доверительными границами, предполагая, что разброс данных (величина дисперсии) в одной серии опытов может быть как больше, так и меньше, чем в другой серии. Используя для сравнения дисперсий значения Fкр из табл. П 2.3 для уровня значимости , получим риск ошибки 2.
Если дисперсии двух серий опытов не отличаются значимо друг от друга, то определить, есть ли статистически значимая разница в результатах серий, можно с помощью t-распределения Стьюдента. Для этого вычисляют среднее взвешенное двух дисперсий:
(4.2)и величину:
(4.3)Далее для числа степеней свободы ν= n1 + n2 - 2 и уровня значимости из табл. П 2.2 или с помощью функции EXCEL СТЬЮДРАСПОБР определяют критическое значение tкр. Если t < tкр, то принимают, что
и являются оценками одного математического ожидания