Файл: Методические указания к лабораторным работам для студентов специальности 140101.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.10.2023
Просмотров: 162
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
– построить график функции 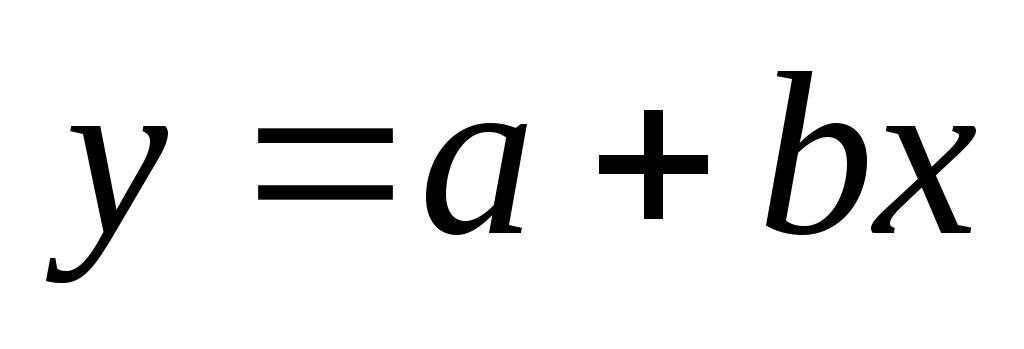 и нанести на него границы доверительных интервалов и экспериментальные точки.
и нанести на него границы доверительных интервалов и экспериментальные точки.
Пример выполнения лабораторной работы
Предположим, что при исследовании влияния независимого параметра х на величину параметра у было проведено восемь опытов и получено восемь пар значений (xi,yi), которые представлены в табл.5.2.
Таблица 5.2. Результаты экспериментов
Выделим Лист5 Книги EXCELдля выполнения работы, запишем в ячейке А1 заголовок работы, в массив В4:С11 из табл. 5.2 занесем исходные данные. Затем в столбцах D4:D11, E4:E11, F4:F11, G4:G11 и H4:H11 вычислим значения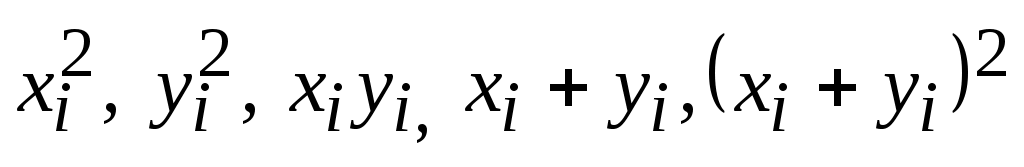 . В ячейках В12:Н12 подсчитаем соответствующие суммы. В ячейке Н13 по формуле =D12+E12+2*F12 вычислим сумму
. В ячейках В12:Н12 подсчитаем соответствующие суммы. В ячейке Н13 по формуле =D12+E12+2*F12 вычислим сумму 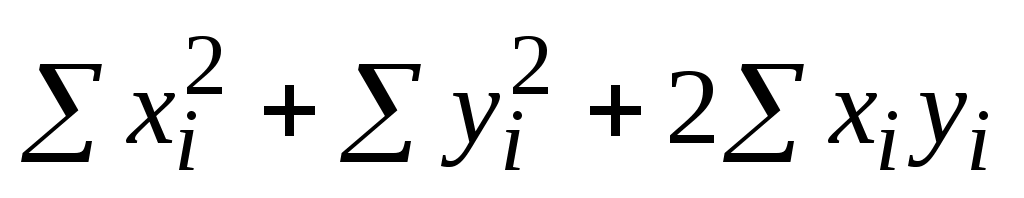 и сравним ее с содержимым ячейки Н12. В ячейках В14 и В15 вычислим средние арифметические
и сравним ее с содержимым ячейки Н12. В ячейках В14 и В15 вычислим средние арифметические  и
и 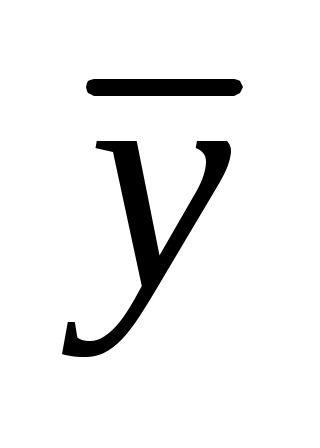 .
.
Формулы (5.8) и (5.9) для определения коэффициентов уравнения регрессии содержат одинаковые знаменатели, поэтому для упрощения расчетов целесообразно сначала вычислить общую часть, а затем результат использовать в отдельных формулах. Активизируем ячейку В16 и введем в нее формулу =A11*D12-B12*B12. Затем в ячейках В17 и В18 вычислим значения коэффициентов а и b, введя формулы =(C12*D12-B12*F12)/B16 и =(A11*F12-B12*C12)/B16. В результате получим а = 4,1667; b = 1,4444. Уравнение регрессии имеет вид
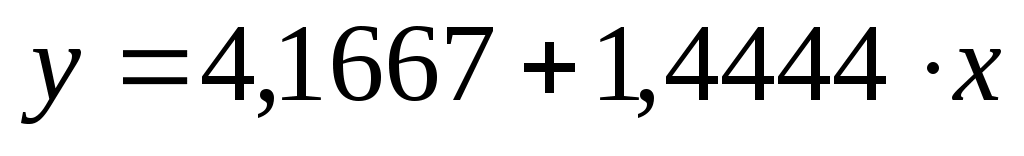 .
.
Проверим адекватность уравнения регрессии, определив в ячейках Е14 и Е15 общую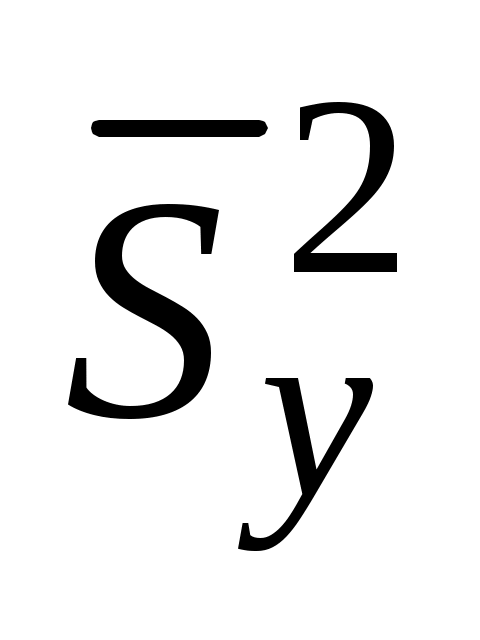 и остаточную
и остаточную 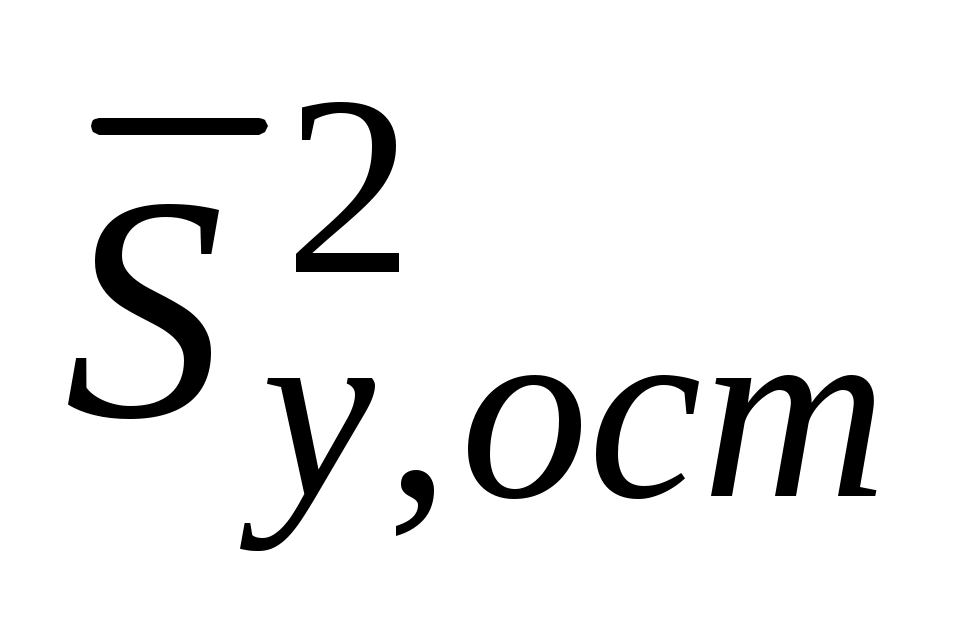 дисперсии. Затем в ячейке Е16 по (5.14) вычислим критерий Фишера. В результате получим F = 4,6692. Активизируем ячейку Е17 и из табл. П 2.3 или с помощью функции FРАСПОБР для α = 0,05; ν1 = 7; ν2 = 6 введем значение Fкр= 4,2067. Так как остаточная дисперсия заведомо должна быть меньше общей, то здесь должен использоваться односторонний критерий.
дисперсии. Затем в ячейке Е16 по (5.14) вычислим критерий Фишера. В результате получим F = 4,6692. Активизируем ячейку Е17 и из табл. П 2.3 или с помощью функции FРАСПОБР для α = 0,05; ν1 = 7; ν2 = 6 введем значение Fкр= 4,2067. Так как остаточная дисперсия заведомо должна быть меньше общей, то здесь должен использоваться односторонний критерий.
В нашем примереF> Fкр, поэтому уравнение регрессии признается адекватным, и этот вывод записывается в ячейку D18.
По найденному уравнению регрессии вычислим значения функции y, соответствующие наблюдаемым значениям параметра х. Активизируем ячейку I4, введем в нее формулу =$B$17+$B$18*B4 и растянем ячейку до I11.
Затем в ячейке Н14 по (5.16) или, используя формулу EXCEL
КОРРЕЛ, вычислим коэффициент корреляции. Для проверки его значимости по (5.17) в ячейке Н15 вычислим значение параметра распределения Стьюдента, записав формулу
=ABS(H14)*КОРЕНЬ((A11-2)/(1-H14^2)). В результате получим tr=5,1657. В ячейку Н16 введем значение критерия Стьюдента, взятое из табл. П 2.2 для α = 0,05 и ν = 6 или найденное с помощью функции =СТЬЮДРАСПОБР(0,05;6). Так как tr > tкр= 2,4469, то коэффициент корреляции признается значимым, и этот вывод записывается в ячейку G18.
Определим доверительные интервалы коэффициентов регрессии. В ячейке В19 вычислим остаточное среднеквадратичное отклонение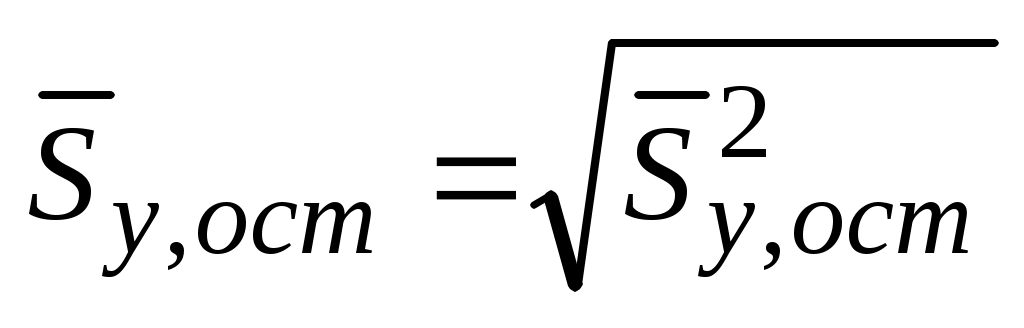 и по (5.20) и (5.21) среднеквадратичные отклонения коэффициентов регрессии
и по (5.20) и (5.21) среднеквадратичные отклонения коэффициентов регрессии 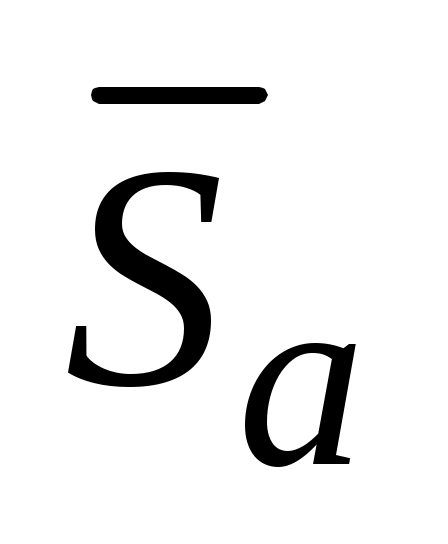 и
и 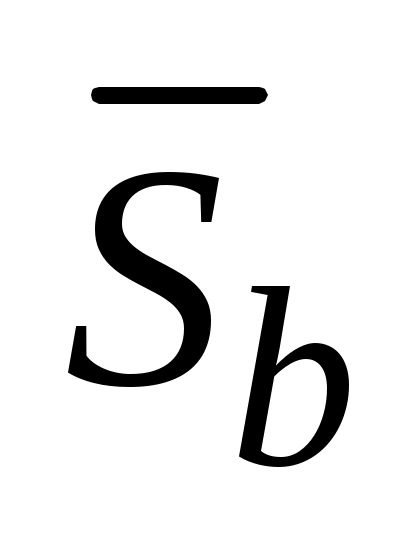 . В ячейках Е20:Е21 и G20:G21 по (5.18) и (5.19) вычислим минимальные и максимальные значения параметров уравнения регрессии.
. В ячейках Е20:Е21 и G20:G21 по (5.18) и (5.19) вычислим минимальные и максимальные значения параметров уравнения регрессии.
Для построения доверительных интервалов сформируем новый массив исходных данных. Наблюдаемый диапазон изменения аргумента х находится в пределах [1,1; 2,2]. Несколько расширим этот диапазон и занесем в ячейки А24:А28 значения аргумента х от 1,0 до 2,4 с шагом 0,1. В ячейках В24:В38 по уравнению регрессии найдем расчетные значения функции. Для определения доверительных интервалов линии регрессии по (5.22) сначала вычислим величину
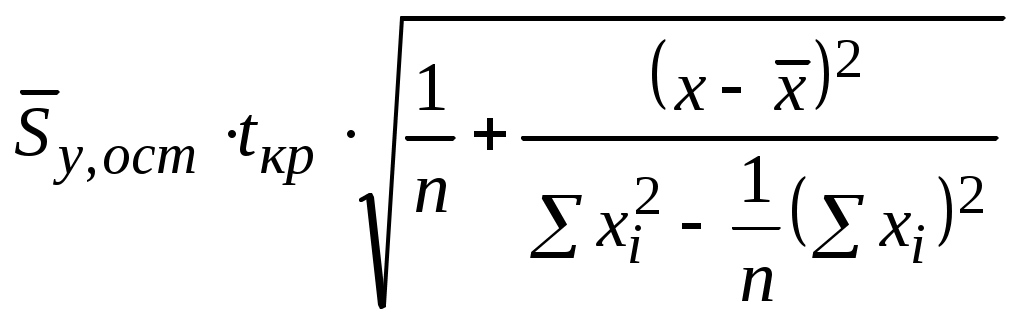 .
.
Для этого в ячейку G24 запишем формулу =$B$19*$H$16*КОРЕНЬ(1/$A$11+(A24-$B$14)^2/($D$12-$B$12*$B$12/$A$11)) и растянем эту ячейку до G38. Затем в ячейки С24 и D24 введем формулы =B24-G24, =B24+G24 и растянем эти ячейки до С38 и D38.
Далее в столбце Е, в строках, соответствующих наблюдаемым значениям аргумента х, введем наблюдаемые значения функции у. Затем выделим массив А24:Е38 и с помощью Мастера диаграмм построим график. Далее перенесем график на свободное место, растянем его до нужного размера и проведем его форматирование. Выберем для линии регрессии сплошную линию без маркеров, для границ доверительных интервалов – пунктирные линии без маркеров, а для экспериментальных значений – маркеры без линии.
Вид рабочего листа лабораторной работы №5 показан на рис.5.1, вид графика – на рис. 5.2. Тот факт, что некоторые экспериментальные значения могут находиться за доверительными границами, не противоречит теории, поскольку границы рассчитываются для математического ожидания (среднего значения) функции, а не для индивидуальных значений yi.
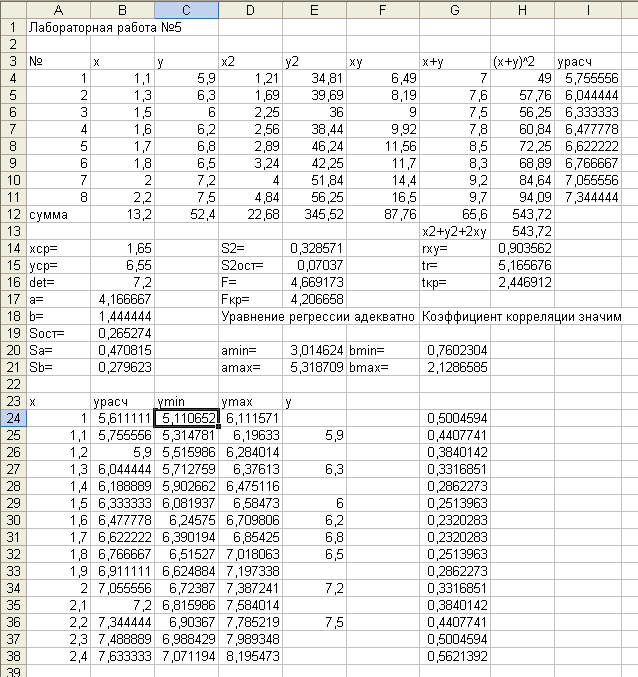
Рис. 5.1. Общий вид листа лабораторной работы №5
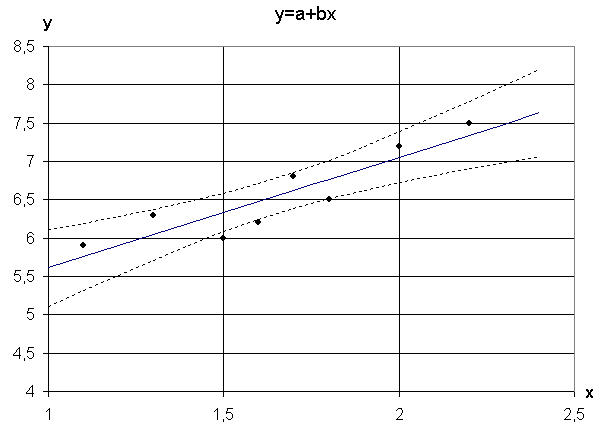
Рис. 5.2. Общий вид графика для линии регрессии
Приложения
Приложение 1
Таблица П 1.1. Варианты заданий к лабораторной работе №3
Таблица П.1.2. Варианты задания №1 к лабораторной работе №4
Пример выполнения лабораторной работы
Предположим, что при исследовании влияния независимого параметра х на величину параметра у было проведено восемь опытов и получено восемь пар значений (xi,yi), которые представлены в табл.5.2.
Таблица 5.2. Результаты экспериментов
| № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
Х | 1,1 | 1,3 | 1,5 | 1,6 | 1,7 | 1,8 | 2 | 2,2 |
У | 5,9 | 6,3 | 6,0 | 6,2 | 6,8 | 6,5 | 7,2 | 7,5 |
Выделим Лист5 Книги EXCELдля выполнения работы, запишем в ячейке А1 заголовок работы, в массив В4:С11 из табл. 5.2 занесем исходные данные. Затем в столбцах D4:D11, E4:E11, F4:F11, G4:G11 и H4:H11 вычислим значения
Формулы (5.8) и (5.9) для определения коэффициентов уравнения регрессии содержат одинаковые знаменатели, поэтому для упрощения расчетов целесообразно сначала вычислить общую часть, а затем результат использовать в отдельных формулах. Активизируем ячейку В16 и введем в нее формулу =A11*D12-B12*B12. Затем в ячейках В17 и В18 вычислим значения коэффициентов а и b, введя формулы =(C12*D12-B12*F12)/B16 и =(A11*F12-B12*C12)/B16. В результате получим а = 4,1667; b = 1,4444. Уравнение регрессии имеет вид
Проверим адекватность уравнения регрессии, определив в ячейках Е14 и Е15 общую
В нашем примереF> Fкр, поэтому уравнение регрессии признается адекватным, и этот вывод записывается в ячейку D18.
По найденному уравнению регрессии вычислим значения функции y, соответствующие наблюдаемым значениям параметра х. Активизируем ячейку I4, введем в нее формулу =$B$17+$B$18*B4 и растянем ячейку до I11.
Затем в ячейке Н14 по (5.16) или, используя формулу EXCEL
КОРРЕЛ, вычислим коэффициент корреляции. Для проверки его значимости по (5.17) в ячейке Н15 вычислим значение параметра распределения Стьюдента, записав формулу
=ABS(H14)*КОРЕНЬ((A11-2)/(1-H14^2)). В результате получим tr=5,1657. В ячейку Н16 введем значение критерия Стьюдента, взятое из табл. П 2.2 для α = 0,05 и ν = 6 или найденное с помощью функции =СТЬЮДРАСПОБР(0,05;6). Так как tr > tкр= 2,4469, то коэффициент корреляции признается значимым, и этот вывод записывается в ячейку G18.
Определим доверительные интервалы коэффициентов регрессии. В ячейке В19 вычислим остаточное среднеквадратичное отклонение
Для построения доверительных интервалов сформируем новый массив исходных данных. Наблюдаемый диапазон изменения аргумента х находится в пределах [1,1; 2,2]. Несколько расширим этот диапазон и занесем в ячейки А24:А28 значения аргумента х от 1,0 до 2,4 с шагом 0,1. В ячейках В24:В38 по уравнению регрессии найдем расчетные значения функции. Для определения доверительных интервалов линии регрессии по (5.22) сначала вычислим величину
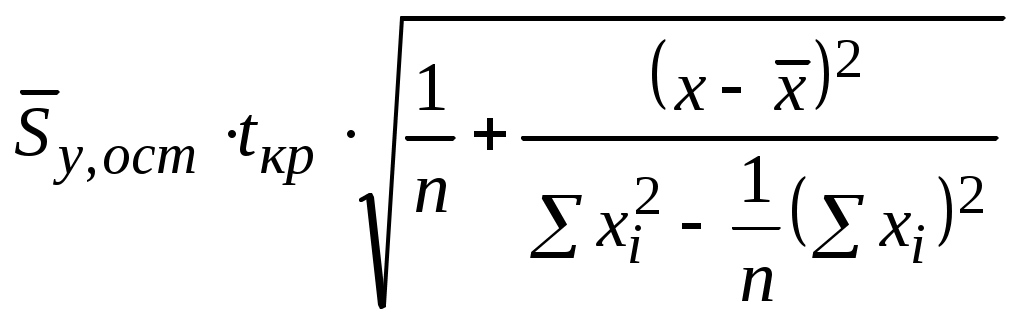 .
. Для этого в ячейку G24 запишем формулу =$B$19*$H$16*КОРЕНЬ(1/$A$11+(A24-$B$14)^2/($D$12-$B$12*$B$12/$A$11)) и растянем эту ячейку до G38. Затем в ячейки С24 и D24 введем формулы =B24-G24, =B24+G24 и растянем эти ячейки до С38 и D38.
Далее в столбце Е, в строках, соответствующих наблюдаемым значениям аргумента х, введем наблюдаемые значения функции у. Затем выделим массив А24:Е38 и с помощью Мастера диаграмм построим график. Далее перенесем график на свободное место, растянем его до нужного размера и проведем его форматирование. Выберем для линии регрессии сплошную линию без маркеров, для границ доверительных интервалов – пунктирные линии без маркеров, а для экспериментальных значений – маркеры без линии.
Вид рабочего листа лабораторной работы №5 показан на рис.5.1, вид графика – на рис. 5.2. Тот факт, что некоторые экспериментальные значения могут находиться за доверительными границами, не противоречит теории, поскольку границы рассчитываются для математического ожидания (среднего значения) функции, а не для индивидуальных значений yi.

Рис. 5.1. Общий вид листа лабораторной работы №5
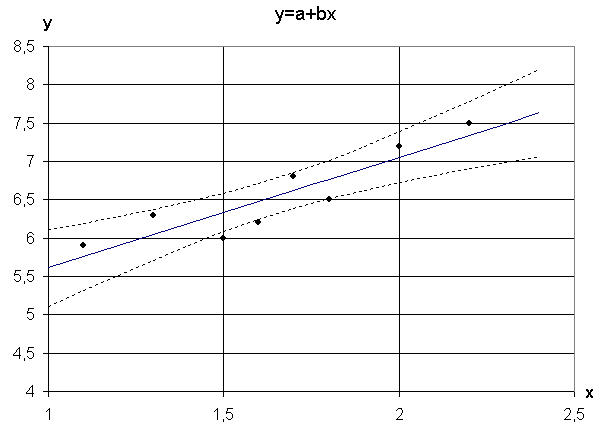
Рис. 5.2. Общий вид графика для линии регрессии
Приложения
Приложение 1
Таблица П 1.1. Варианты заданий к лабораторной работе №3
| Номер варианта | Результаты измерений | |||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| 1 | 1,37 | 1,43 | 1,38 | 1,42 | 1,54 | 1,35 | 1,34 | 1,35 | 1,36 | 1,37 | 1,36 | 1,31 |
| 2 | 12,3 | 17,4 | 11,8 | 14,2 | 13,5 | 11,5 | 13,4 | 14,2 | 14,3 | 10,7 | 12,6 | 12,3 |
| 3 | 43,1 | 18,2 | 60,5 | 28,3 | 35,4 | 30,2 | 33,4 | 48,7 | 42,4 | 39,2 | 53,2 | 47,0 |
| 4 | 43,1 | 48,2 | 60,5 | 44,3 | 45,4 | 50,2 | 43,4 | 48,7 | 42,4 | 39,2 | 53,2 | 47,0 |
| 5 | 3,42 | 2,72 | 2,15 | 2,88 | 2,87 | 2,92 | 2,84 | 3,07 | 2,84 | 3,02 | 2,97 | 2,67 |
| 6 | 143 | 132 | 111 | 108 | 122 | 116 | 118 | 108 | 111 | 117 | 123 | 113 |
| 7 | 143 | 132 | 111 | 114 | 122 | 116 | 118 | 119 | 111 | 117 | 123 | 113 |
| 8 | 343 | 332 | 331 | 314 | 332 | 339 | 338 | 335 | 323 | 341 | 344 | 340 |
| 9 | 1,07 | 1,11 | 1,23 | 1,19 | 1,09 | 1,07 | 1,09 | 1,12 | 1 ,10 | 1,09 | 1,10 | 1,11 |
| 10 | 10,7 | 9,98 | 10,2 | 10,1 | 10,0 | 9,97 | 10,1 | 10,2 | 10,1 | 10,2 | 10,1 | 9,38 |
| 11 | 5,61 | 5,59 | 5,38 | 5,60 | 5,58 | 5,60 | 5,59 | 5,57 | 5,59 | 5,62 | 5,58 | 5,59 |
| 12 | 16,3 | 15,8 | 15,9 | 16,2 | 15,7 | 15,8 | 15,9 | 16,9 | 15,7 | 15,8 | 15,8 | 15,8 |
| 13 | 32,2 | 31,7 | 30,4 | 32,2 | 31,9 | 32,0 | 32,1 | 31 ,9 | 32,1 | 32,1 | 31,9 | 32,1 |
| 14 | 352 | 331 | 343 | 311 | 342 | 337 | 339 | 342 | 335 | 338 | 340 | 338 |
| 15 | 81 ,7 | 80,9 | 81,3 | 82,1 | 84,2 | 80,8 | 81,3 | 82,2 | 81 ,4 | 82,0 | 82,0 | 82,1 |
| 16 | 72,3 | 69,7 | 74,2 | 71,8 | 70,5 | 63,4 | 70,7 | 72,2 | 80,4 | 71,3 | 72,1 | 68,1 |
| 17 | 525 | 518 | 515 | 522 | 517 | 505 | 517 | 519 | 538 | 519 | 522 | 523 |
| 18 | 328 | 331 | 330 | 332 | 329 | 338 | 321 | 327 | 330 | 327 | 312 | 329 |
| 19 | 2,48 | 2,52 | 2,46 | 2,47 | 2,60 | 2,44 | 2,45 | 2,50 | 2,51 | 2,42 | 2,68 | 2,47 |
| 20 | 13,7 | 14,1 | 14,3 | 13,9 | 10,0 | 13,2 | 14,0 | 14,1 | 16,3 | 12,9 | 13,4 | 13,7 |
| 21 | 66,2 | 63,1 | 65,4 | 68,1 | 62,1 | 53,8 | 69,7 | 66,6 | 65,1 | 62,7 | 52,1 | 67,3 |
| 22 | 47,3 | 46,9 | 42,1 | 46,7 | 45,9 | 47,0 | 46,9 | 45,7 | 47,1 | 46,7 | 71,2 | 46,5 |
| 23 | 213 | 215 | 212 | 202 | 209 | 214 | 212 | 215 | 222 | 217 | 212 | 214 |
| 24 | 422 | 423 | 428 | 422 | 422 | 411 | 425 | 420 | 419 | 427 | 418 | 417 |
| 25 | 772 | 767 | 770 | 758 | 767 | 771 | 769 | 770 | 768 | 780 | 772 | 769 |
| 26 | 7,23 | 7,19 | 7,25 | 7,18 | 7,22 | 7,12 | 7,23 | 7,20 | 7,21 | 7,33 | 7,19 | 7,20 |
| 27 | 51,4 | 50,9 | 51,6 | 52,7 | 51,3 | 51,0 | 51,1 | 50,8 | 51,1 | 51,3 | 51,2 | 51,2 |
| 28 | 73,9 | 71,1 | 72,2 | 77,3 | 73,3 | 72,7 | 72,5 | 73,1 | 70,4 | 72,8 | 73,0 | 73,2 |
| 29 | 412 | 448 | 436 | 413 | 425 | 3,48 | 416 | 415 | 403 | 450 | 411 | 422 |
| 30 | 375 | 377 | 368 | 337 | 382 | 371 | 369 | 370 | 365 | 393 | 313 | 370 |
Таблица П.1.2. Варианты задания №1 к лабораторной работе №4
| Номер варианта | Данные первой серии | Данные второй серии | Паспортные данные | ||||
| | n1 | | | n2 | | a | |
| 1 | 16,0 | 4 | 9,28 | 18,3 | 9 | 3,43 | 20 |
| 2 | 77,0 | 7 | 6,32 | 74 | 4 | 15,5 | 80 |
| 3 | 892,0 | 3 | 293,1 | 905,0 | 14 | 143,2 | 920 |
| 4 | 51,7 | 4 | 4,32 | 59,3 | 13 | 3,12 | 60 |
| 5 | 12,4 | 4 | 5,67 | 11,3 | 15 | 4,13 | 10 |
| 6 | 45,9 | 7 | 25,7 | 48,3 | 5 | 18,5 | 50 |
| 7 | 78,1 | 6 | 1,32 | 75,4 | 3 | 6,38 | 80 |
| 8 | 33,2 | 8 | 3,78 | 31,5 | 5 | 10,92 | 35 |
| 9 | 68,1 | 7 | 4,56 | 68,3 | 8 | 2,17 | 70 |
| 10 | 221,3 | 5 | 14,13 | 220,7 | 11 | 49,17 | 225 |
| 11 | 327,2 | 4 | 4,782 | 325,3 | 12 | 3,29 | 330 |
| 12 | 48,9 | 12 | 3,22 | 45,3 | 4 | 14,71 | 50 |
| 13 | 17,9 | 5 | 3,12 | 15,6 | 15 | 12,7 | 20 |
| 14 | 95,3 | 7 | 12,17 | 97,2 | 14 | 4,12 | 100 |
| 15 | 139,4 | 4 | 55,2 | 146,5 | 11 | 27,3 | 150 |
| 16 | 682,3 | 3 | 91,3 | 692,9 | 7 | 33,13 | 700 |
| 17 | 325,4 | 3 | 10,7 | 319,5 | 7 | 47,3 | 330 |
| 18 | 62,4 | 8 | 7,13 | 61,3 | 4 | 19,2 | 60 |
| 19 | 13,2 | 5 | 3,13 | 14,4 | 13 | 1,02 | 15 |
| 20 | 77,2 | 10 | 12,13 | 73,5 | 5 | 32,9 | 80 |
| 21 | 483,0 | 9 | 87,37 | 475,0 | 4 | 128,3 | 500 |
| 22 | 743,0 | 13 | 40,13 | 737,1 | 5 | 143,8 | 750 |
| 23 | 22,1 | 3 | 8,78 | 24,2 | 15 | 3,81 | 25 |
| 24 | 63,1 | 5 | 3,12 | 64,8 | 9 | 0,78 | 65 |
| 25 | 102,5 | 17 | 10,6 | 106,6 | 5 | 43,2 | 100 |
| 26 | 37,4 | 11 | 9,87 | 39,2 | 5 | 33,9 | 35 |
| 27 | 17,6 | 5 | 10,45 | 18,4 | 7 | 4,12 | 20 |
| 28 | 53,4 | 4 | 10,52 | 51,7 | 11 | 2,17 | 50 |
| 29 | 92,4 | 13 | 4,7 | 95,6 | 4 | 19,4 | 90 |
| 30 | 9,1 | 3 | 2,33 | 9,6 | 11 | 0,43 | 10 |