Файл: Методические указания к лабораторным работам для студентов специальности 140101.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.10.2023
Просмотров: 163
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, т.е. различие между ними статистически незначимо. В противном случае с вероятностью ошибки считают, что они статистически неодинаковы.
В тех случаях, когда средние значения исследуемой величины х статистически неразличимы, можно объединить обе серии опытов, рассматривая n1 + n2 результатов как данные одной серии. Суммарное среднее арифметическое будет равно
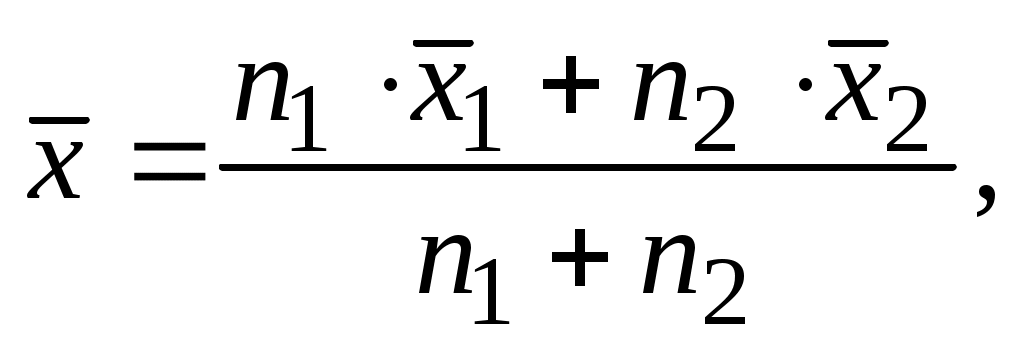 (4.4)
(4.4)
суммарная дисперсия
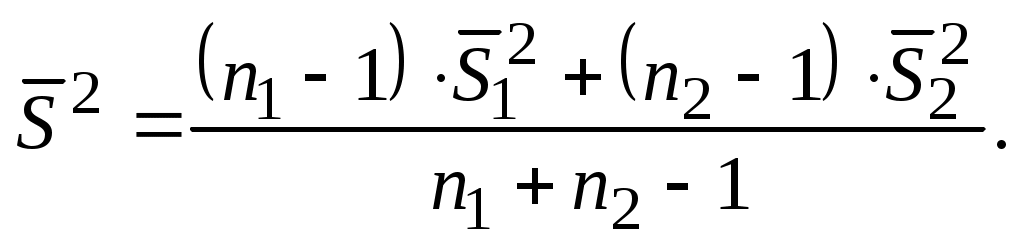 (4.5)
(4.5)
Частным случаем является сравнение среднего арифметического с постоянной величиной. Такая задача встречается, когда некоторую величину, вычисленную теоретически или заданную нормативными характеристиками, необходимо проверить экспериментально. В этом случае имеется только одно среднее арифметическое и одна дисперсия
и одна дисперсия  . Для сравнения полученного результата с заданной величиной вычисляют параметр распределения Стьюдента:
. Для сравнения полученного результата с заданной величиной вычисляют параметр распределения Стьюдента:
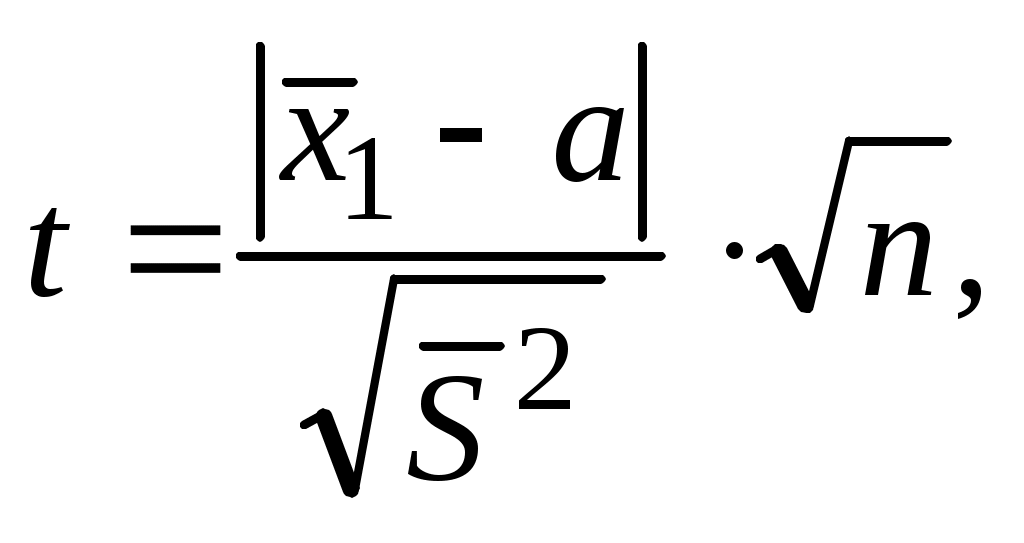 (4.6)
(4.6)
где а – величина, с которой сравнивают результаты измерений.
Критерий tкр для принятого уровня значимости и числа степеней свободы ν= n – l определяют из табл. П. 2.2 или с помощью функции EXCEL СТЬЮДРАСПОБР. При t > tкр можно утверждать, что наблюдаемое значение значимо отличается от нормативной величины а.
значимо отличается от нормативной величины а.
При неравноточных измерениях, когда F > Fкр, при n1 = n2 = n проверку однородности результатов в двух сериях опытов можно осуществить лишь приближенно. В этом случае вычисляют параметр
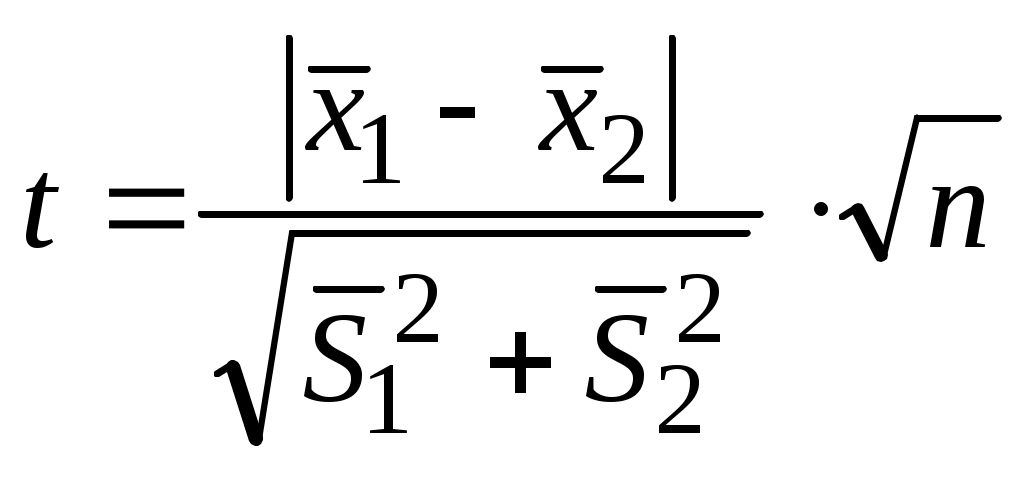 . (4.7)
. (4.7)
Для выбора критического значения tкр число степеней свободы ν вычисляют по формуле
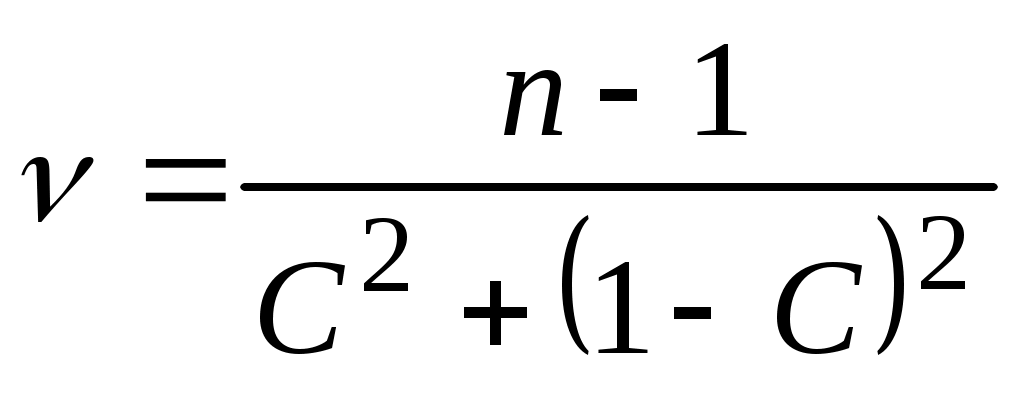 , (4.8)
, (4.8)
где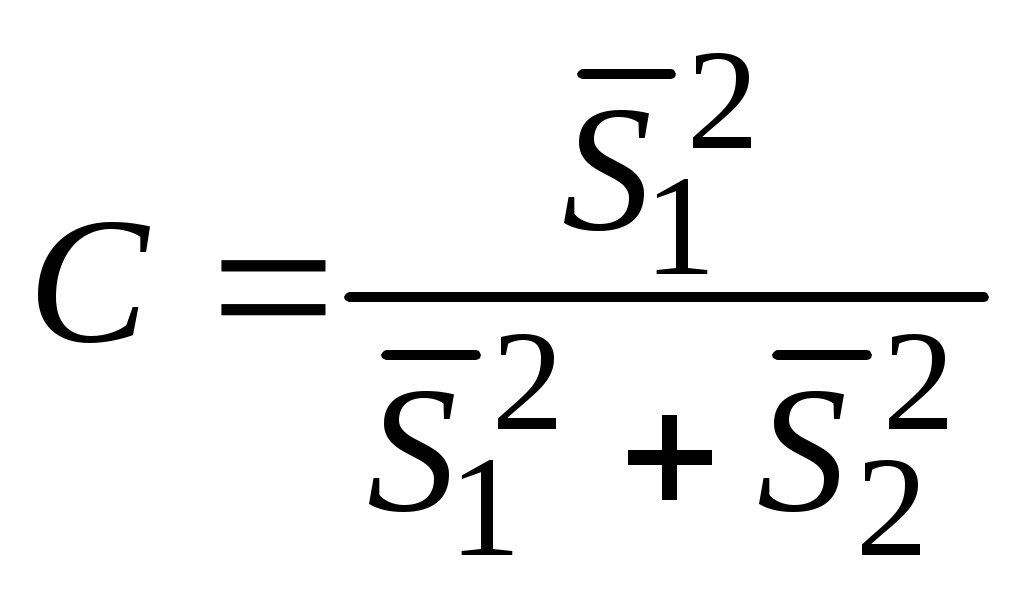 .
.
Для оценки однородности дисперсий k серий опытов с числом степеней свободы ν1, ν2
, …, νk применяется критерий Бартлетта:
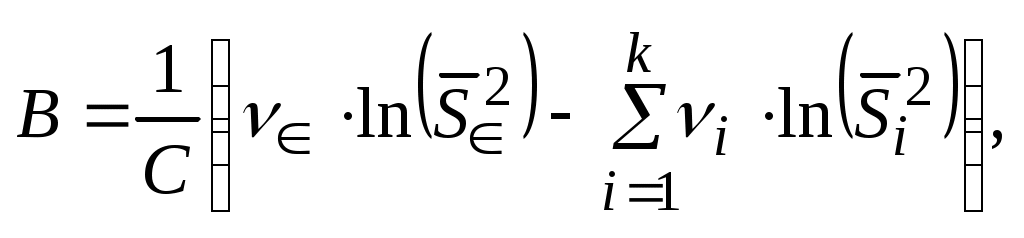 (4.9)
(4.9)
где средняя взвешенная дисперсия определяется выражением
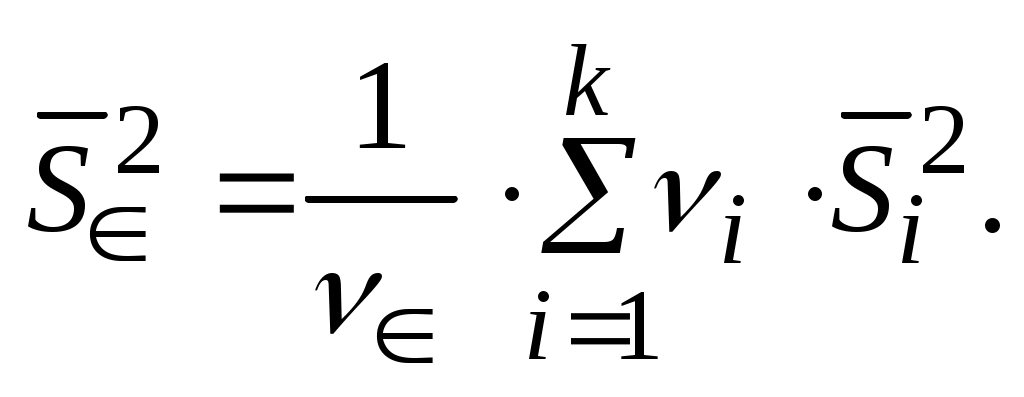 (4.10)
(4.10)
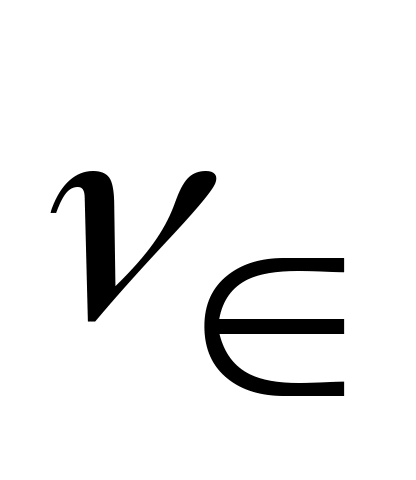 – суммарное число степеней свободы:
– суммарное число степеней свободы:
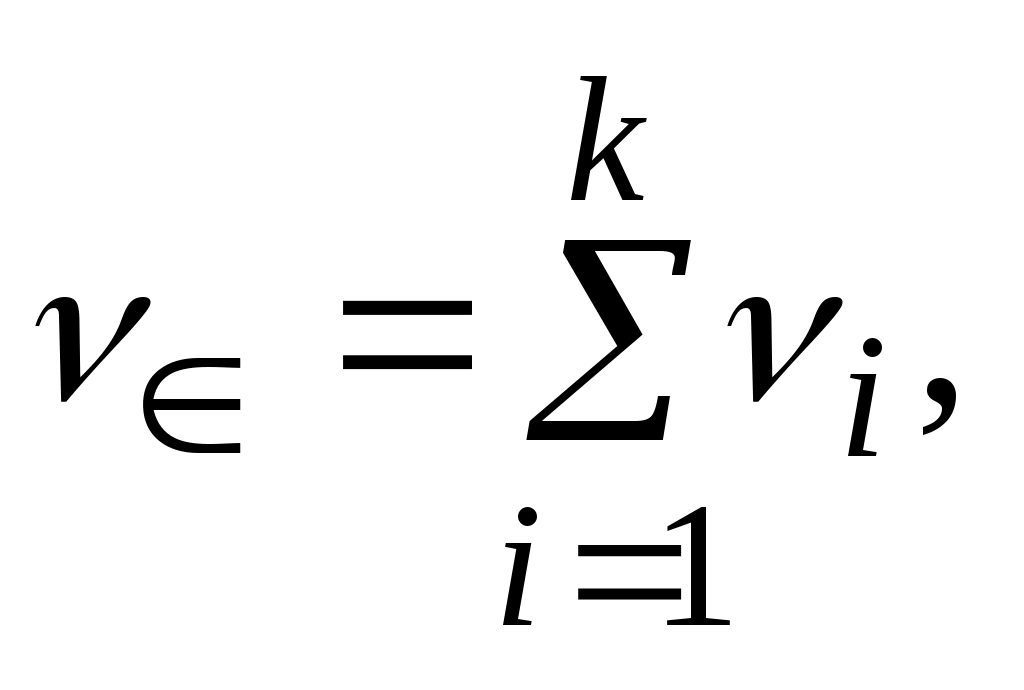 (4.11)
(4.11)
а параметр С рассчитывается по формуле
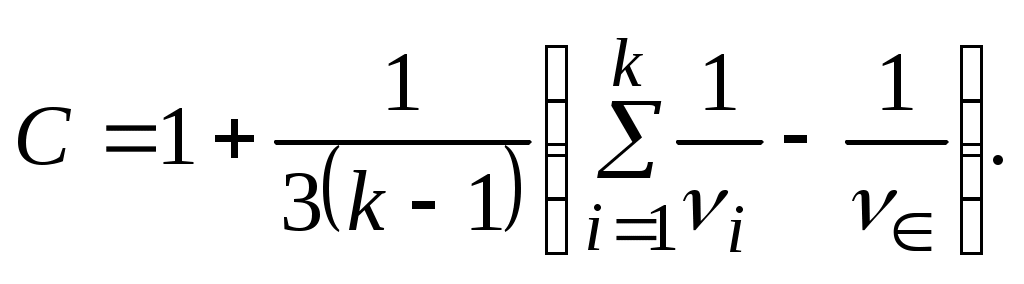 (4.12)
(4.12)
Критерий Бартлетта имеет распределение 2 с k-1 степенями свободы. Если найденная величина критерия В превосходит значение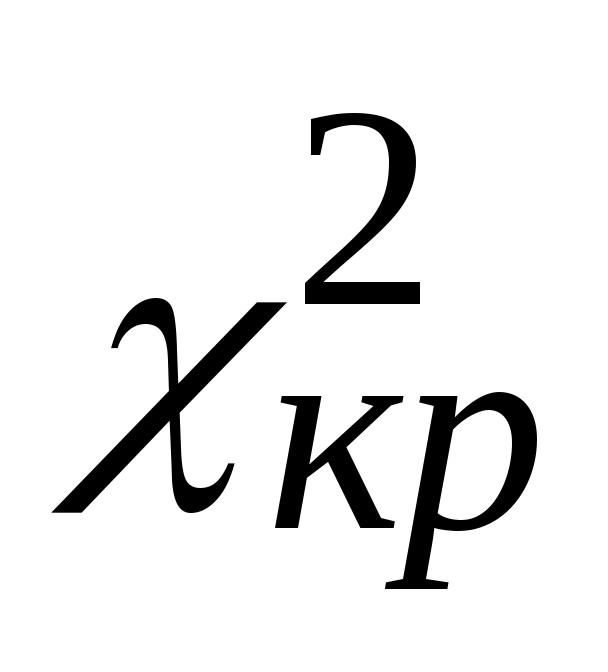 при выбранном уровне значимости, то дисперсии результатов в разных сериях опытов статистически неоднородны (измерения неравноточны). Значение
при выбранном уровне значимости, то дисперсии результатов в разных сериях опытов статистически неоднородны (измерения неравноточны). Значение 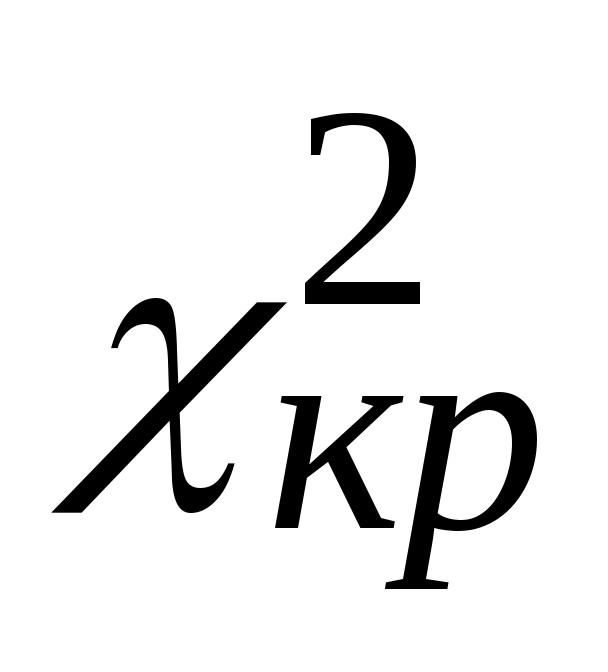 определяется по уровню значимости и числу степеней свободы ν = k - l из табл. П.2.4. или с помощью функции EXCEL ХИ2ОБР.
определяется по уровню значимости и числу степеней свободы ν = k - l из табл. П.2.4. или с помощью функции EXCEL ХИ2ОБР.
При одинаковом объеме измерений в каждой из серий опытов (n1=n2= …=n) для сравнения дисперсий используется более точный критерий Кохрена, равный отношению максимальной дисперсии к сумме всех дисперсий:
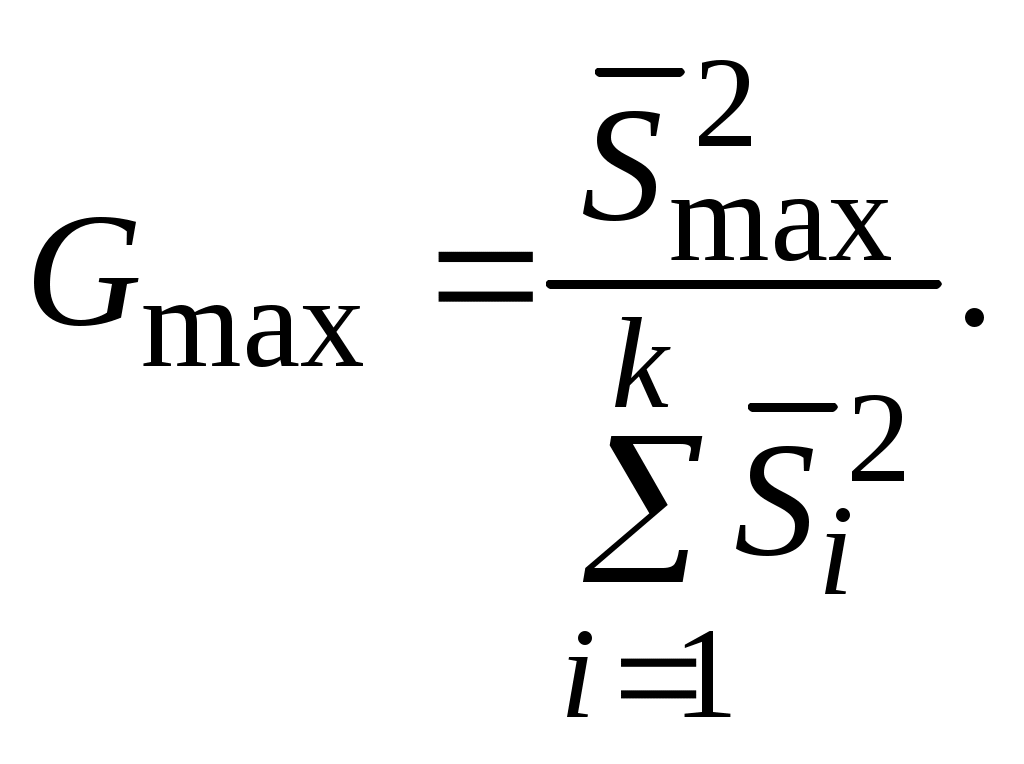 (4.13)
(4.13)
Рассчитанное по (4.13) значение Gmax сравнивают с критической величиной критерия Gкр, значения которого для уровней значимости =0,05 и 0,01, числа степеней свободы ν = n - l и количества серий опытов k приведены в табл. П 2.5.
При Gmax > Gкр гипотезу об однородности дисперсий отвергают с риском ошибки .
Задание на лабораторную работу
Оценки выполнить для уровня значимости α = 0,05.
Пример выполнения лабораторной работы
Задание 1
По паспортным данным некоторый параметр установки х должен иметь значение х0=65. Для экспериментальной проверки было проведено две серии опытов с n1=7 и n2=5 параллельными измерениями. В результате экспериментов были получены значения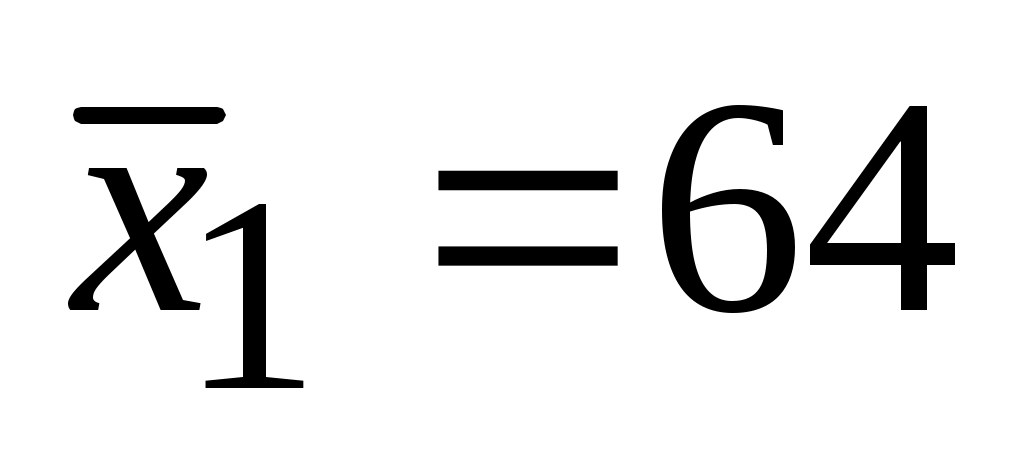 при
при 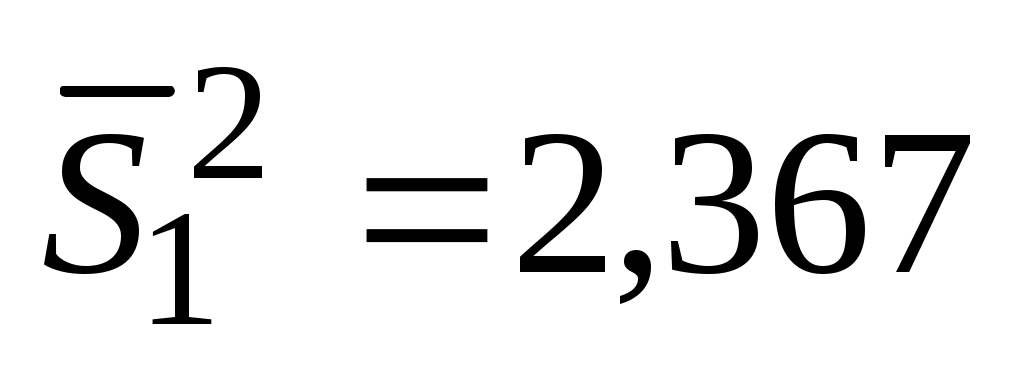 и
и 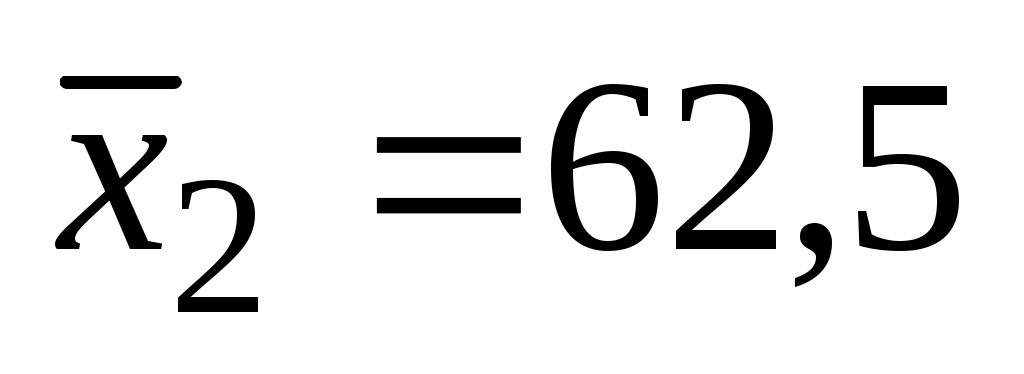 при
при 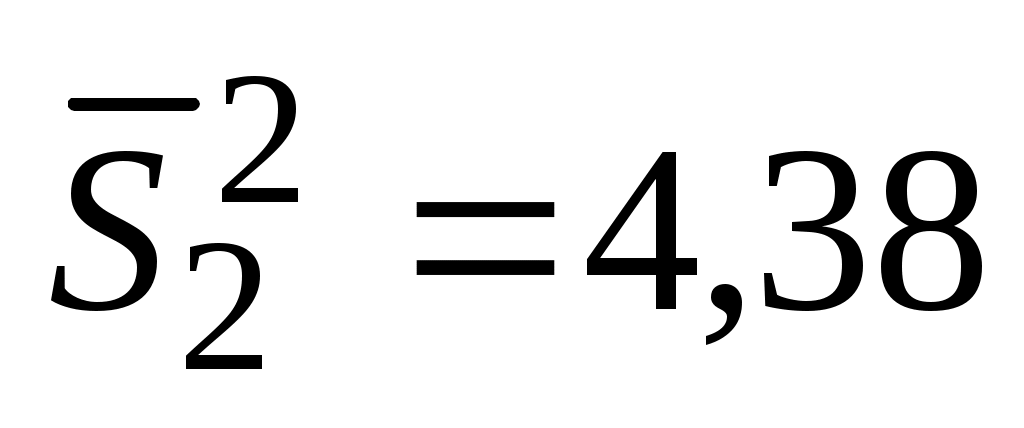 .
.
Выделим Лист4 Книги EXCELдля выполнения работы, запишем в ячейке А1 заголовок работы, в ячейке А2 укажем заголовок Задание1 а в массив В3:В9 занесем исходные данные соответственно 64; 7; 2,367; 62,5; 5; 4,38; 65.
Определим, являются ли измерения в сериях опытов равноточными. Запишем в ячейку С3 заголовок критерия Фишера. Так как наибольшая дисперсия наблюдалась во второй серии опытов, то активизируем ячейку D4 и введем формулу =B6/B4. Получим значение критерия 1,8504. Число степеней свободы распределения соответственно равны ν1= 5-1=4, ν2=7-1=6.
В табл. П 2.3. приведены односторонние значения Фишера. В данном случае нет оснований предполагать, что точность измерений в одной серии опытов должна быть выше, чем в другой, поэтому необходимо рассматривать двухсторонние ограничения, взяв критерий Фишера для уровня значимости α/2=0,025.
Так как для этого уровня данных в таблице нет, возьмем значения критерия для ближайших уровней и проведем линейную интерполяцию:
Fкр(0,05; 4; 6) = 4,534; Fкр(0,01; 4; 6) = 9,148;
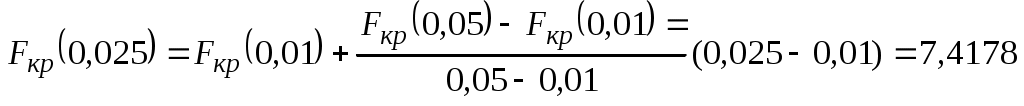 .
.
Значение критерия также можно найти, используя функцию =FРАСПОБР(0,025;4;6), которая выведет значение 6,2272. Столь заметное различие значений критерия, полученных интерполяцией и с помощью функции объясняется погрешностью линейной интерполяции при существенно нелинейной зависимости.
Так как F= 1,8504 < Fкр =6,2272, делаем вывод о том, что измерения в двух сериях опытов являются равноточными, и записываем этот вывод в ячейку С5.
Сравним средние значения в сериях опытов между собой. Для этого по (4.2) вычислим среднее взвешенное двух дисперсий, записав в ячейку В11 формулу =((B4-1)*B5+(B7-1)*B8)/(B4+B7-2). В результате в ячейке получим значение 3,1722. Далее в ячейке D7 по (4.3)
вычислим значение критерия Стьюдента, записав формулу
=ABS(B6-B3)/КОРЕНЬ(B11)*КОРЕНЬ(B4*B7/(B4+B7))
В результате вычисления получим значение 1,4383. Для числа степеней свободы ν = n1+ n2 -2 = 10 и α = 0,05 из табл. П 2.2 или с помощью функции =СТЬЮДРАСПОБР(0,05;10) найдем и запишем в ячейку D8 значение tкр= 2,2281.
Так как t = 1,4383 < tкр= 2,2281, то делаем заключение, что различия средних значений в обеих сериях опытов статистически незначимы, и записываем это заключение в ячейку С9.
Далее проверяем, значимо ли расхождение между паспортными и экспериментальными значениями параметра х.
Сравниваем результаты первой серии опытов с паспортным значением. В ячейке G7 вычисляем параметр t1, введя формулу =ABS(B3-B9)*КОРЕНЬ(B4/B5). В результате получим значение критерия
t1= 1,7196. В ячейке G8 находим значение критерия Стьюдента для
α = 0,05 и ν = 6: t1кр=2,4469. Так как t1 = < t1кр, то принимаем, что результаты первой серии опытов согласуются с паспортными данными, и записываем этот вывод в ячейку А13.
Сравниваем результаты второй серии опытов с паспортным значением. В ячейке I7 вычисляем значение критерия t2= 2.6711, в ячейке I8 для α = 0,05 и ν = 4 находим табличное значение критерия t2кр=2,7764. Так как t2 = < t2кр, то принимаем, что результаты второй серии опытов также согласуются с паспортными данными, и записываем этот вывод в ячейку А14.
Так как результаты двух серий опытов различаются между собой статистически незначимо, а измерения признаны равноточными, то можно представить их результаты как совокупность результатов одного эксперимента с n1 + n2 = 12 параллельными измерениями величины х. Определим средневзвешенные результаты совокупности опытов, записав в ячейке I10 формулу =(B3*B4+B6*B7)/(B4+B7). В результате вычисления получим:
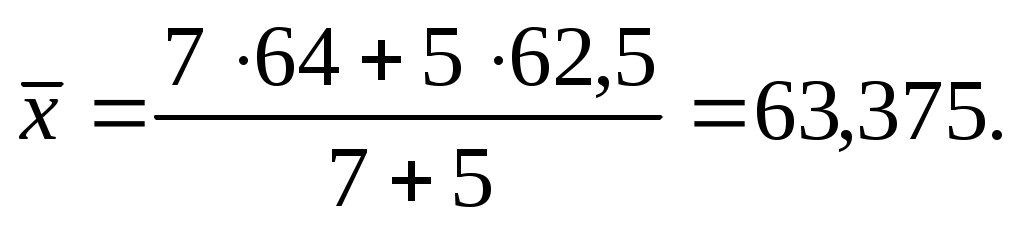
В ячейке I11 по (4.5) вычислим суммарную дисперсию, записав формулу =(B5*(B4-1)+B8*(B7-1))/(B4+B7-1). В результате получим:
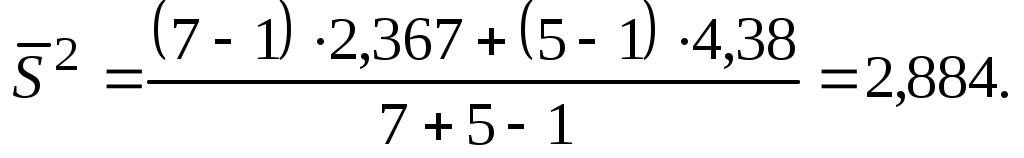
По (4.6) в ячейке I12 вычислим критерий Стьюдента:
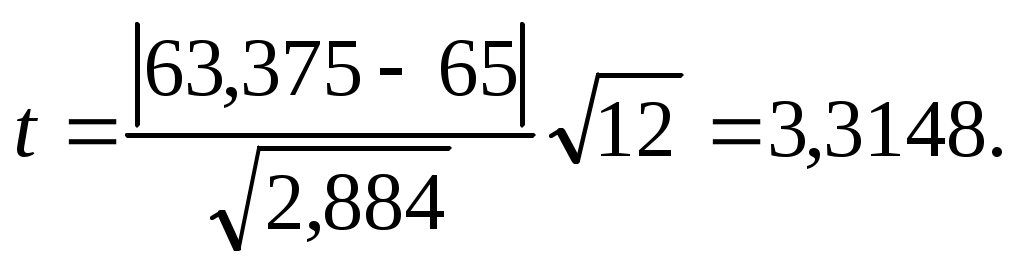
В ячейке I13 для α = 0,05 и ν = 11 находим табличное значение критерия tкр=2,2010.
В данном случае t = 3,3148 > tкр = 2,2010. Это свидетельствует о том, что результаты эксперимента значимо отличаются от паспортных данных. С вероятностью ошибки = 5% можно утверждать, что во время экспериментов параметр х принимал меньшие значения, чем указано в паспорте установки. Такой вывод оказалось возможным сделать только при использовании результатов экспериментов обеих серий, поскольку при раздельном анализе из-за небольшого количества опытов в каждой из серий паспортное и экспериментальные значения параметра х оказались статистически неразличимыми.
Задание 2
Во время испытаний установки на нескольких режимах были проведены измерения параметра Х. Всего было исследовано 7 режимов, причем в каждом из них для повышения надежности результатов измерения дублировались: n1 = 4; n2 = 6; n3 = 7; n4 = 5; n5=4; n6 = 6; n7 = 5. При обработке результатов были найдены дисперсии: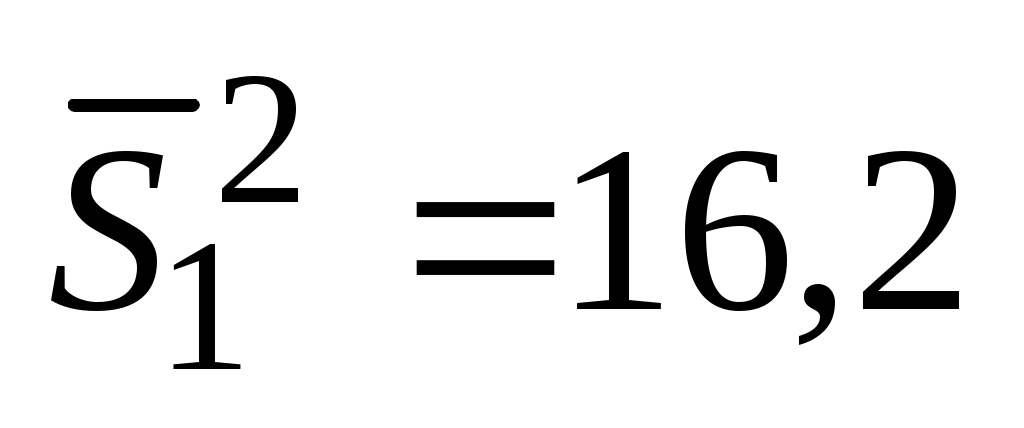 ;
; 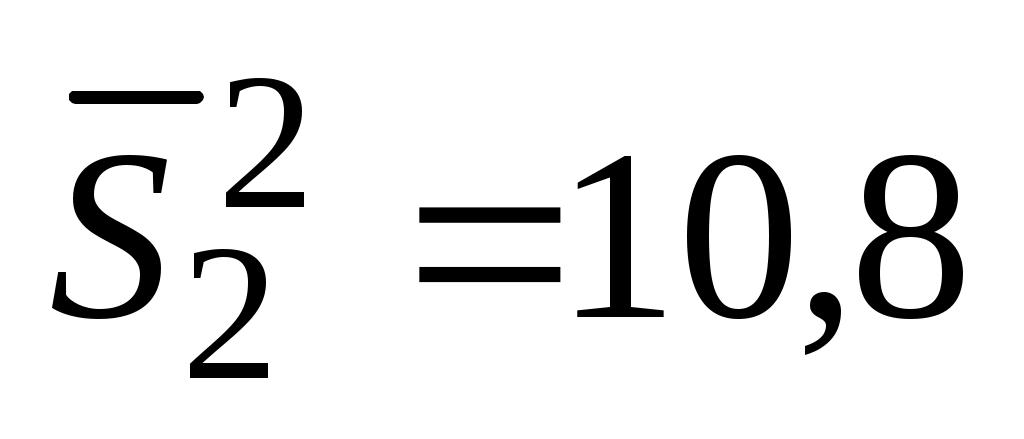 ;
; 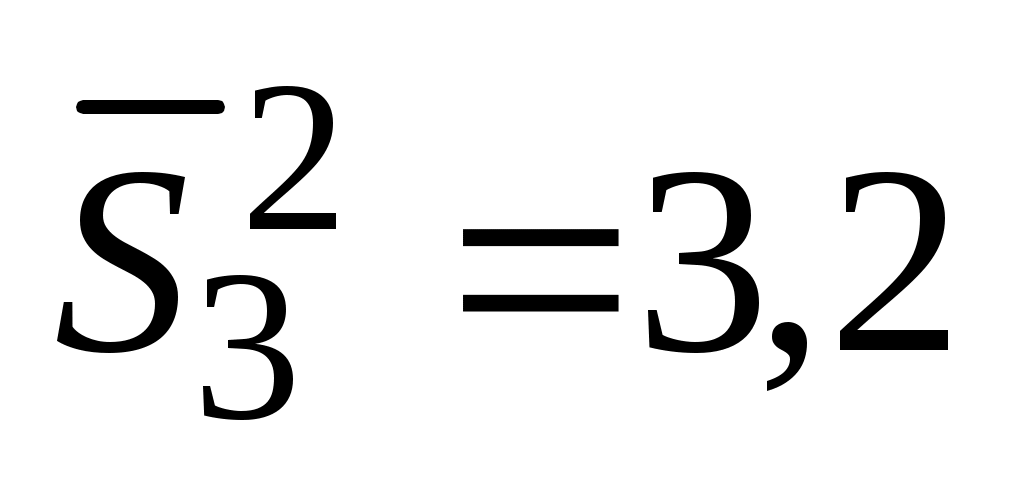 ;
; 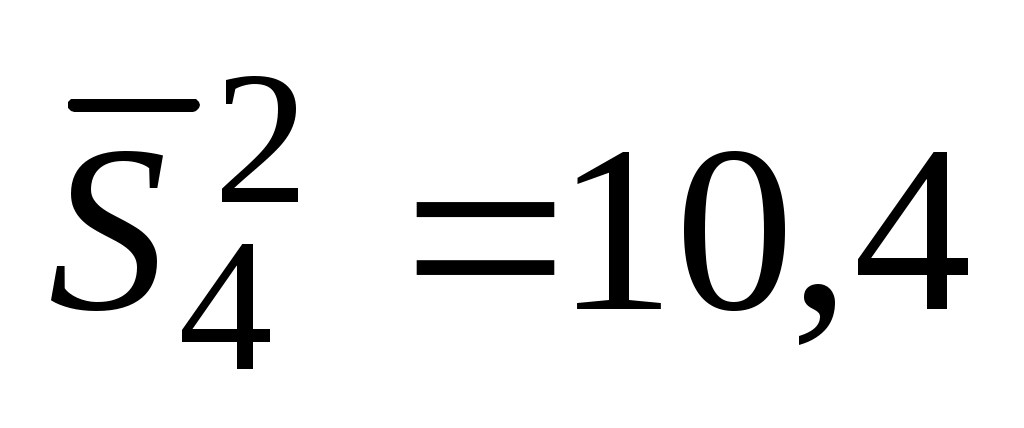 ;
; 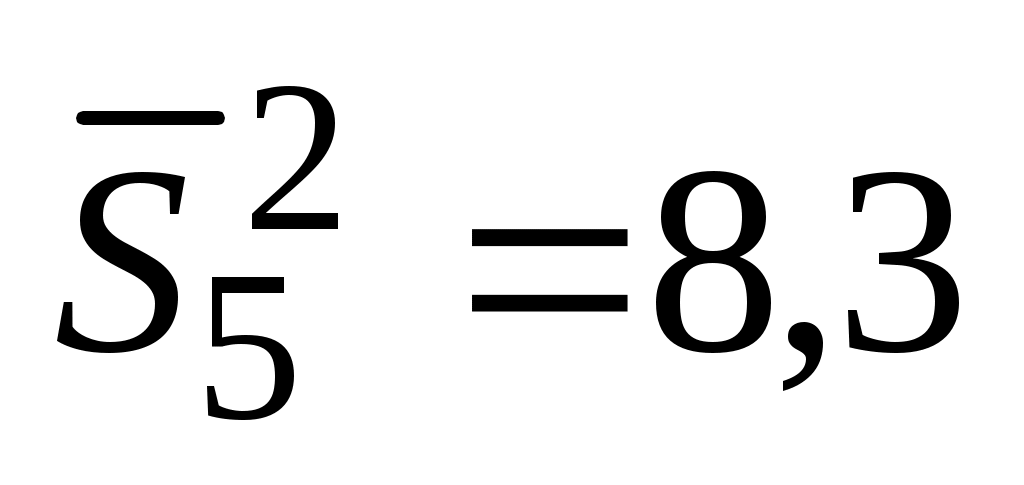 ;
; 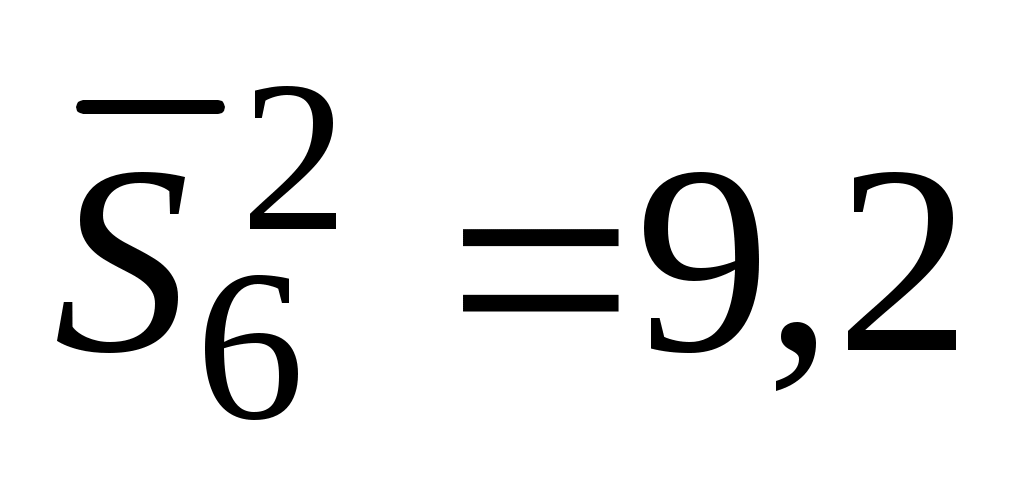 ;
; 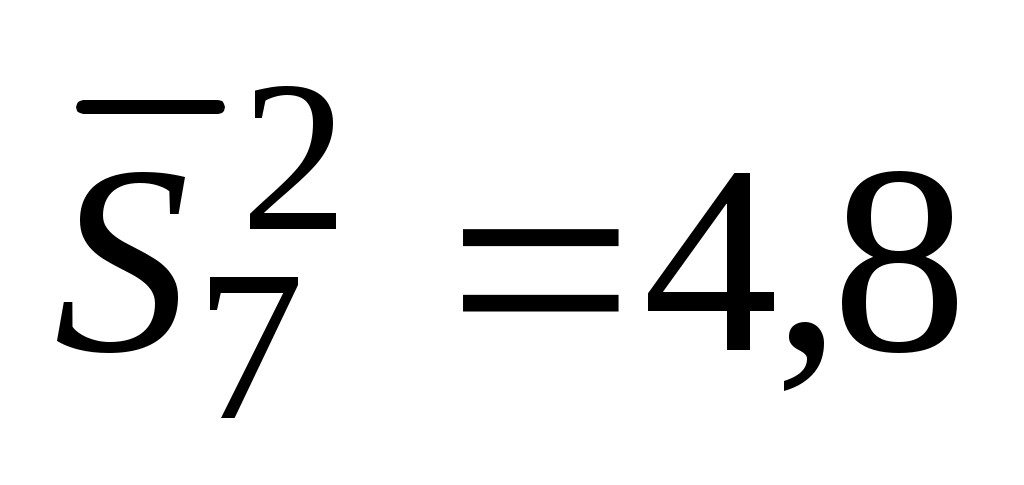 . Требуется определить, можно ли считать измерения на разных режимах равноточными.
. Требуется определить, можно ли считать измерения на разных режимах равноточными.
Запишем в ячейке А16 заголовок Задание2 и в ячейки В17:С24 введем исходные данные. Поскольку количество параллельных измерений на различных режимах неодинаково, то для оценки однородности дисперсий воспользуемся критерием Бартлетта. Для расчета критерия по (4.9) в ячейках D18:D24 вычислим числа степеней свободы ν, в ячейках Е18:Е24 найдем их обратные величины 1/ν, в ячейках F18:F24 вычислим произведение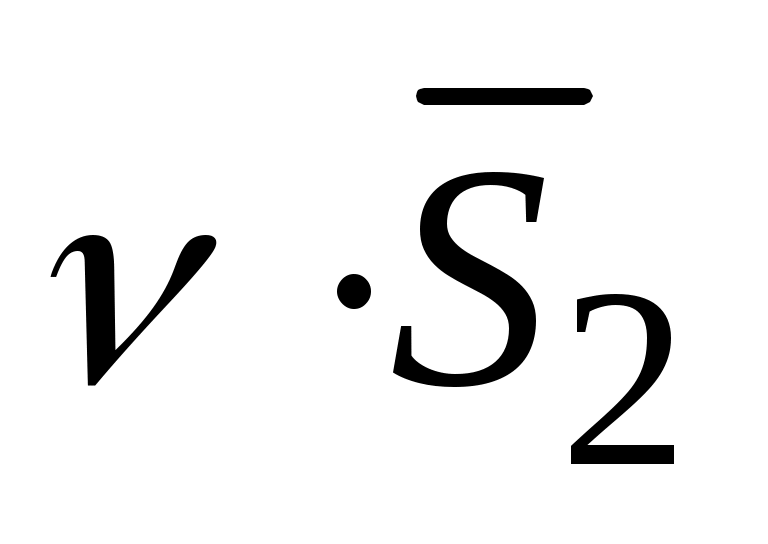 , а в ячейках G18:G24 – произведение
, а в ячейках G18:G24 – произведение 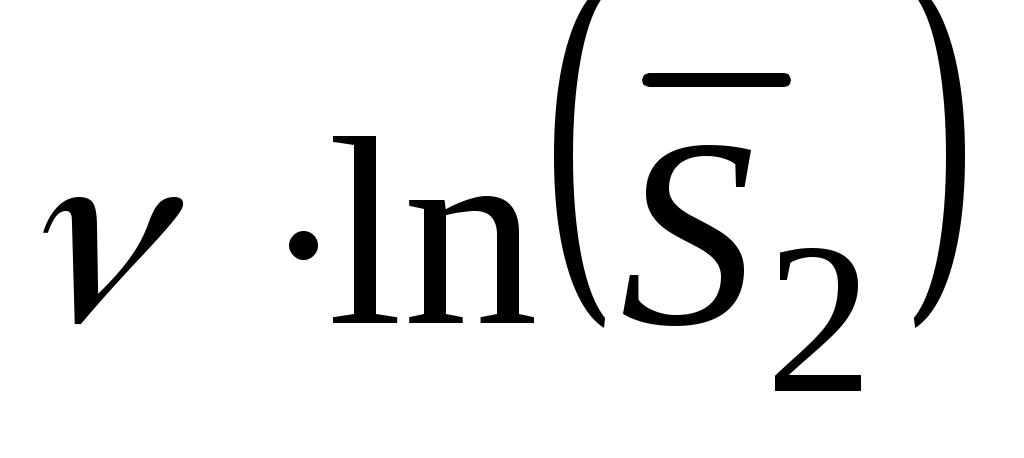 . В ячейках С25:G25 вычислим суммы значений в соответствующих столбцах.
. В ячейках С25:G25 вычислим суммы значений в соответствующих столбцах.
Далее в ячейке I17 по (4.12) определим значение параметра С, введя формулу =1+1/3/(7-1)*(E25-1/D25). В ячейке I18 по (4.10) найдем значение средневзвешенной дисперсии
В тех случаях, когда средние значения исследуемой величины х статистически неразличимы, можно объединить обе серии опытов, рассматривая n1 + n2 результатов как данные одной серии. Суммарное среднее арифметическое будет равно
суммарная дисперсия
Частным случаем является сравнение среднего арифметического с постоянной величиной. Такая задача встречается, когда некоторую величину, вычисленную теоретически или заданную нормативными характеристиками, необходимо проверить экспериментально. В этом случае имеется только одно среднее арифметическое
где а – величина, с которой сравнивают результаты измерений.
Критерий tкр для принятого уровня значимости и числа степеней свободы ν= n – l определяют из табл. П. 2.2 или с помощью функции EXCEL СТЬЮДРАСПОБР. При t > tкр можно утверждать, что наблюдаемое значение
При неравноточных измерениях, когда F > Fкр, при n1 = n2 = n проверку однородности результатов в двух сериях опытов можно осуществить лишь приближенно. В этом случае вычисляют параметр
Для выбора критического значения tкр число степеней свободы ν вычисляют по формуле
где
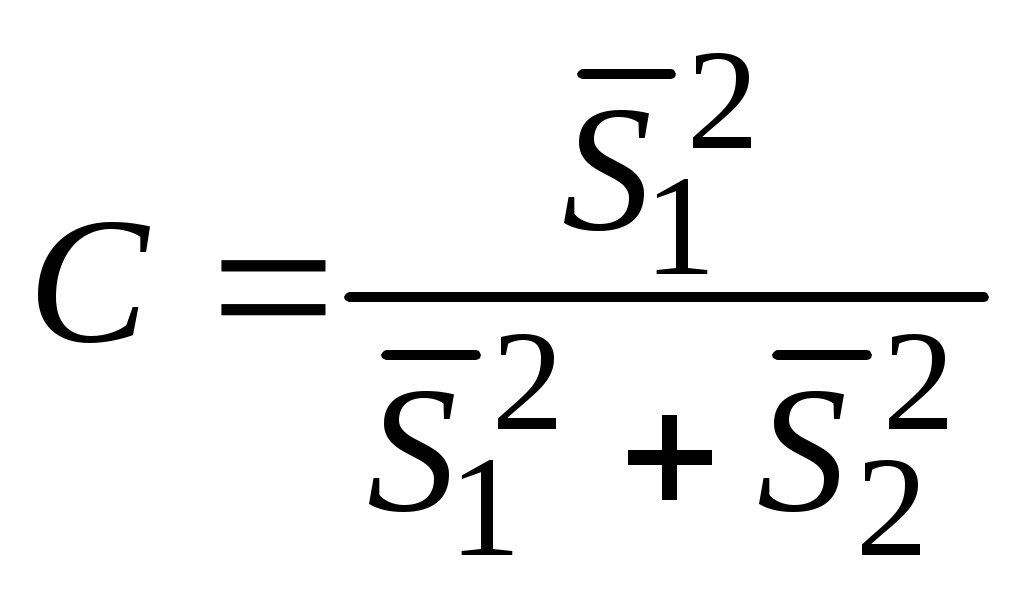 .
.Для оценки однородности дисперсий k серий опытов с числом степеней свободы ν1, ν2
, …, νk применяется критерий Бартлетта:
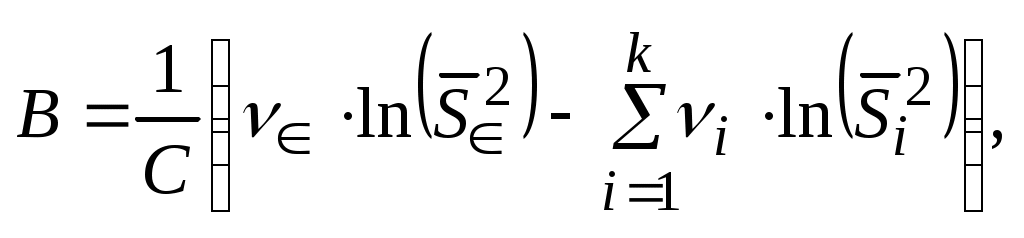 (4.9)
(4.9)где средняя взвешенная дисперсия определяется выражением
а параметр С рассчитывается по формуле
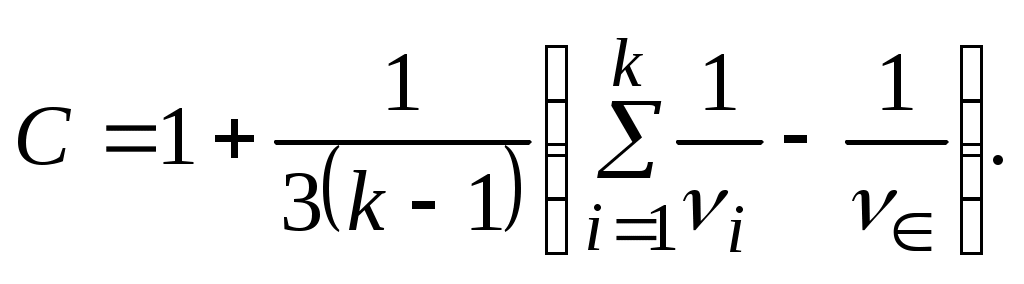 (4.12)
(4.12)Критерий Бартлетта имеет распределение 2 с k-1 степенями свободы. Если найденная величина критерия В превосходит значение
При одинаковом объеме измерений в каждой из серий опытов (n1=n2= …=n) для сравнения дисперсий используется более точный критерий Кохрена, равный отношению максимальной дисперсии к сумме всех дисперсий:
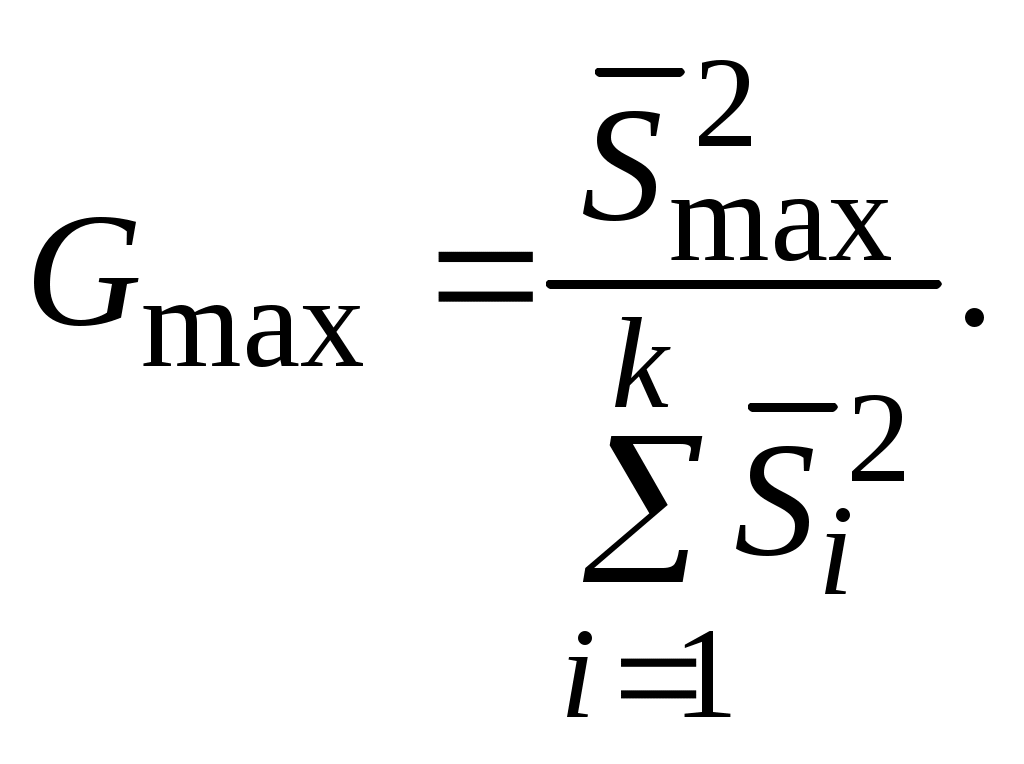 (4.13)
(4.13)Рассчитанное по (4.13) значение Gmax сравнивают с критической величиной критерия Gкр, значения которого для уровней значимости =0,05 и 0,01, числа степеней свободы ν = n - l и количества серий опытов k приведены в табл. П 2.5.
При Gmax > Gкр гипотезу об однородности дисперсий отвергают с риском ошибки .
Задание на лабораторную работу
-
Для варианта исходных данных в табл. П 1.2 определить:
-
значимо ли расхождение в результатах серий опытов; -
подтверждают ли результаты экспериментов паспортные данные на установку;
-
Для варианта исходных данных в табл. П 1.3 проверить равноточность измерений во всех режимах. -
Для этого же варианта проверить равноточность измерений при условии, что в каждом режиме проводилось одинаковое количество дублирующих измерений. Их количество принять равным количеству измерений в первой серии опытов.
Оценки выполнить для уровня значимости α = 0,05.
Пример выполнения лабораторной работы
Задание 1
По паспортным данным некоторый параметр установки х должен иметь значение х0=65. Для экспериментальной проверки было проведено две серии опытов с n1=7 и n2=5 параллельными измерениями. В результате экспериментов были получены значения
Выделим Лист4 Книги EXCELдля выполнения работы, запишем в ячейке А1 заголовок работы, в ячейке А2 укажем заголовок Задание1 а в массив В3:В9 занесем исходные данные соответственно 64; 7; 2,367; 62,5; 5; 4,38; 65.
Определим, являются ли измерения в сериях опытов равноточными. Запишем в ячейку С3 заголовок критерия Фишера. Так как наибольшая дисперсия наблюдалась во второй серии опытов, то активизируем ячейку D4 и введем формулу =B6/B4. Получим значение критерия 1,8504. Число степеней свободы распределения соответственно равны ν1= 5-1=4, ν2=7-1=6.
В табл. П 2.3. приведены односторонние значения Фишера. В данном случае нет оснований предполагать, что точность измерений в одной серии опытов должна быть выше, чем в другой, поэтому необходимо рассматривать двухсторонние ограничения, взяв критерий Фишера для уровня значимости α/2=0,025.
Так как для этого уровня данных в таблице нет, возьмем значения критерия для ближайших уровней и проведем линейную интерполяцию:
Fкр(0,05; 4; 6) = 4,534; Fкр(0,01; 4; 6) = 9,148;
Значение критерия также можно найти, используя функцию =FРАСПОБР(0,025;4;6), которая выведет значение 6,2272. Столь заметное различие значений критерия, полученных интерполяцией и с помощью функции объясняется погрешностью линейной интерполяции при существенно нелинейной зависимости.
Так как F= 1,8504 < Fкр =6,2272, делаем вывод о том, что измерения в двух сериях опытов являются равноточными, и записываем этот вывод в ячейку С5.
Сравним средние значения в сериях опытов между собой. Для этого по (4.2) вычислим среднее взвешенное двух дисперсий, записав в ячейку В11 формулу =((B4-1)*B5+(B7-1)*B8)/(B4+B7-2). В результате в ячейке получим значение 3,1722. Далее в ячейке D7 по (4.3)
вычислим значение критерия Стьюдента, записав формулу
=ABS(B6-B3)/КОРЕНЬ(B11)*КОРЕНЬ(B4*B7/(B4+B7))
В результате вычисления получим значение 1,4383. Для числа степеней свободы ν = n1+ n2 -2 = 10 и α = 0,05 из табл. П 2.2 или с помощью функции =СТЬЮДРАСПОБР(0,05;10) найдем и запишем в ячейку D8 значение tкр= 2,2281.
Так как t = 1,4383 < tкр= 2,2281, то делаем заключение, что различия средних значений в обеих сериях опытов статистически незначимы, и записываем это заключение в ячейку С9.
Далее проверяем, значимо ли расхождение между паспортными и экспериментальными значениями параметра х.
Сравниваем результаты первой серии опытов с паспортным значением. В ячейке G7 вычисляем параметр t1, введя формулу =ABS(B3-B9)*КОРЕНЬ(B4/B5). В результате получим значение критерия
t1= 1,7196. В ячейке G8 находим значение критерия Стьюдента для
α = 0,05 и ν = 6: t1кр=2,4469. Так как t1 = < t1кр, то принимаем, что результаты первой серии опытов согласуются с паспортными данными, и записываем этот вывод в ячейку А13.
Сравниваем результаты второй серии опытов с паспортным значением. В ячейке I7 вычисляем значение критерия t2= 2.6711, в ячейке I8 для α = 0,05 и ν = 4 находим табличное значение критерия t2кр=2,7764. Так как t2 = < t2кр, то принимаем, что результаты второй серии опытов также согласуются с паспортными данными, и записываем этот вывод в ячейку А14.
Так как результаты двух серий опытов различаются между собой статистически незначимо, а измерения признаны равноточными, то можно представить их результаты как совокупность результатов одного эксперимента с n1 + n2 = 12 параллельными измерениями величины х. Определим средневзвешенные результаты совокупности опытов, записав в ячейке I10 формулу =(B3*B4+B6*B7)/(B4+B7). В результате вычисления получим:
В ячейке I11 по (4.5) вычислим суммарную дисперсию, записав формулу =(B5*(B4-1)+B8*(B7-1))/(B4+B7-1). В результате получим:
По (4.6) в ячейке I12 вычислим критерий Стьюдента:
В ячейке I13 для α = 0,05 и ν = 11 находим табличное значение критерия tкр=2,2010.
В данном случае t = 3,3148 > tкр = 2,2010. Это свидетельствует о том, что результаты эксперимента значимо отличаются от паспортных данных. С вероятностью ошибки = 5% можно утверждать, что во время экспериментов параметр х принимал меньшие значения, чем указано в паспорте установки. Такой вывод оказалось возможным сделать только при использовании результатов экспериментов обеих серий, поскольку при раздельном анализе из-за небольшого количества опытов в каждой из серий паспортное и экспериментальные значения параметра х оказались статистически неразличимыми.
Задание 2
Во время испытаний установки на нескольких режимах были проведены измерения параметра Х. Всего было исследовано 7 режимов, причем в каждом из них для повышения надежности результатов измерения дублировались: n1 = 4; n2 = 6; n3 = 7; n4 = 5; n5=4; n6 = 6; n7 = 5. При обработке результатов были найдены дисперсии:
Запишем в ячейке А16 заголовок Задание2 и в ячейки В17:С24 введем исходные данные. Поскольку количество параллельных измерений на различных режимах неодинаково, то для оценки однородности дисперсий воспользуемся критерием Бартлетта. Для расчета критерия по (4.9) в ячейках D18:D24 вычислим числа степеней свободы ν, в ячейках Е18:Е24 найдем их обратные величины 1/ν, в ячейках F18:F24 вычислим произведение
Далее в ячейке I17 по (4.12) определим значение параметра С, введя формулу =1+1/3/(7-1)*(E25-1/D25). В ячейке I18 по (4.10) найдем значение средневзвешенной дисперсии