Файл: Методические указания к лабораторным работам для студентов специальности 140101.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.10.2023
Просмотров: 161
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, а в ячейке I19 вычислим значение критерия Бартлетта, введя формулу =1/I17*(D25*LN(I18)-G25). В итоге получаем значение критерия В=3,3870.
Затем в ячейку I20 запишем значение критерия Пирсона
χ2= 12,5960, найденное по табл. П 2.4 или с помощью функции ХИ2ОБР для = 0,05 и ν = 6.
Так как В < 2 = 12,6, то измерения признаются равноточными. Этот вывод записывается в ячейку А26.
Задание 3
Считаем, что во всех опытах проводилось по 4 опыта. Записываем в ячейку А28 заголовок Задание3. Далее определяем, что наибольший разброс данных (наибольшая дисперсия) наблюдался в первой серии опытов, копируем значение дисперсии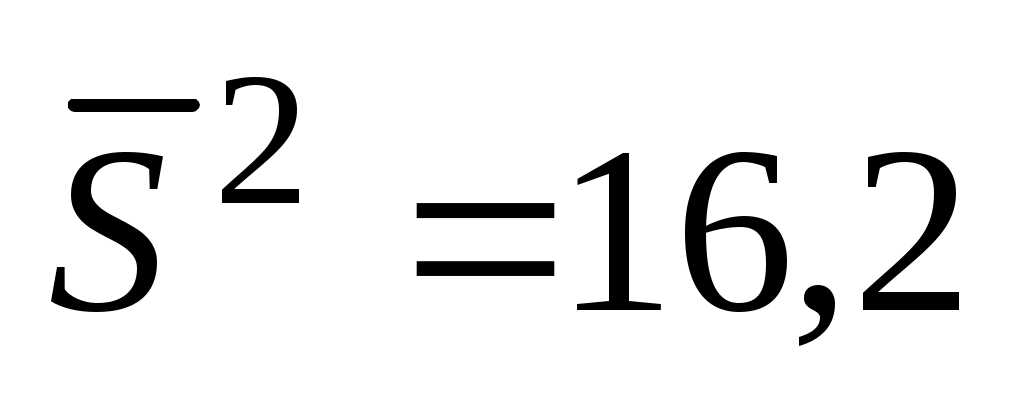 в ячейку В29, в ячейку В30 из ячейки С25 переносим сумму дисперсий и в ячейке В31 по (4.13) вычисляем значение критерия Кохрена:
в ячейку В29, в ячейку В30 из ячейки С25 переносим сумму дисперсий и в ячейке В31 по (4.13) вычисляем значение критерия Кохрена:
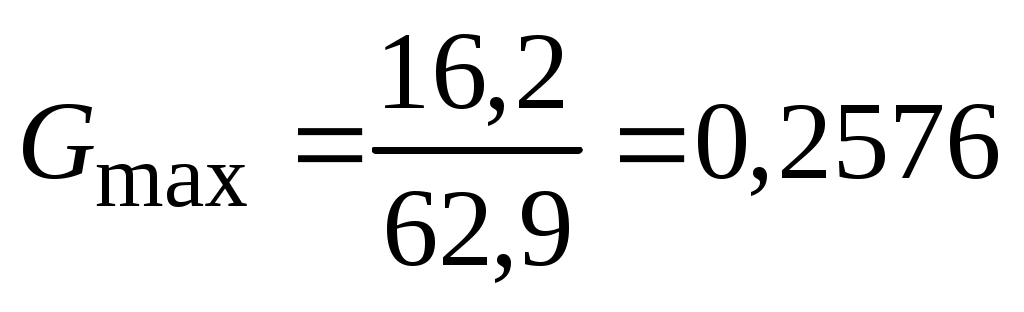 .
.
В ячейку В32 запишем значение Gкр=0,480, найденное по
табл. П 2.5 для = 0,05, ν = n–1 = 3 и k = 7.
Так как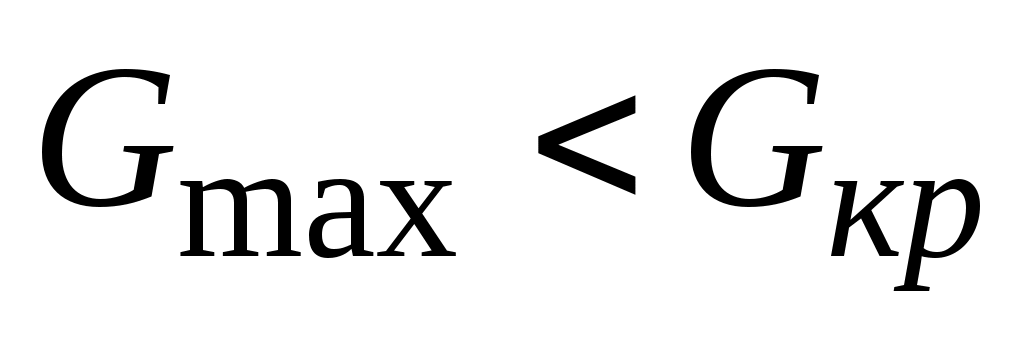 , то признаем измерения равноточными и заносим этот вывод в ячейку А33.
, то признаем измерения равноточными и заносим этот вывод в ячейку А33.
Общий вид рабочего листа лабораторной работы №4 показан на рис. 4.1.
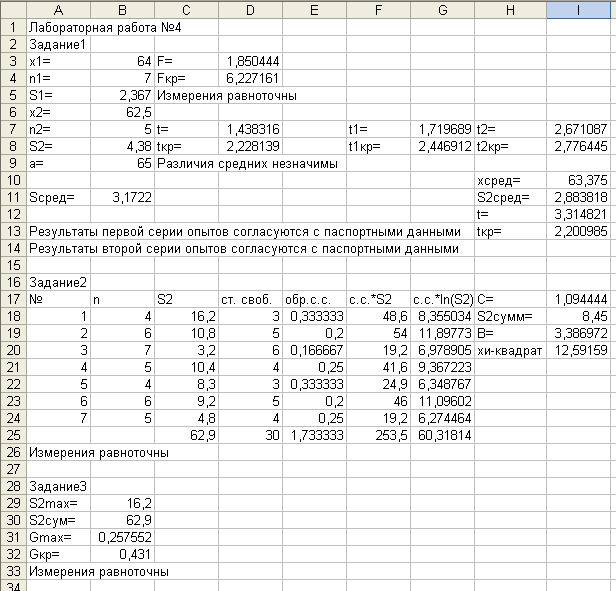
Рис. 4.1. Общий вид второй части лабораторной работы № 4
Лабораторная работа №5
Сглаживание результатов экспериментов
и построение парных линейных зависимостей
методом наименьших квадратов
Допустим, что для исследования взаимосвязи величин х и y были проведены n измерений и получен набор n пар значений xi и yi. Экспериментальные точки дают некоторый разброс относительно истинных значений, связанный с наличием случайных ошибок. При интерпретации этих данных необходимо ответить на следующие вопросы:
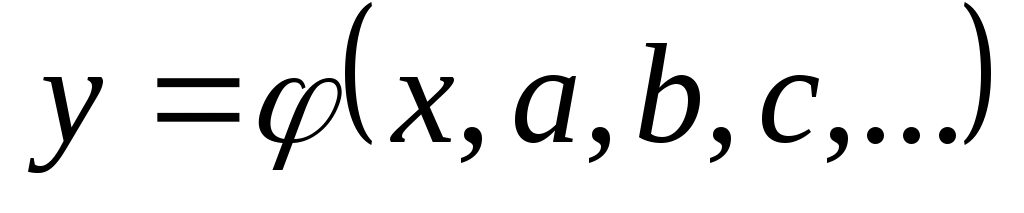 , (5.1)
, (5.1)
описывает результаты эксперимента?
Экспериментальные данные желательно обработать так, чтобы по возможности точно отразить общую тенденцию зависимости y от x и вместе с тем сгладить отклонения, связанные с влиянием случайных неконтролируемых факторов. Задача сводится к выбору типа зависимости (5.1), чтобы эта зависимость в некотором смысле наилучшим образом отображала экспериментальные данные. Уравнение (5.1) называется уравнением регрессии, а параметры a, b, c … – коэффициентами регрессии.
Метод наименьших квадратов предполагает, что наилучшим приближением считается такое, при котором достигается минимум суммы квадратов отклонений расчетных и наблюдаемых значений y, то есть выполняется условие
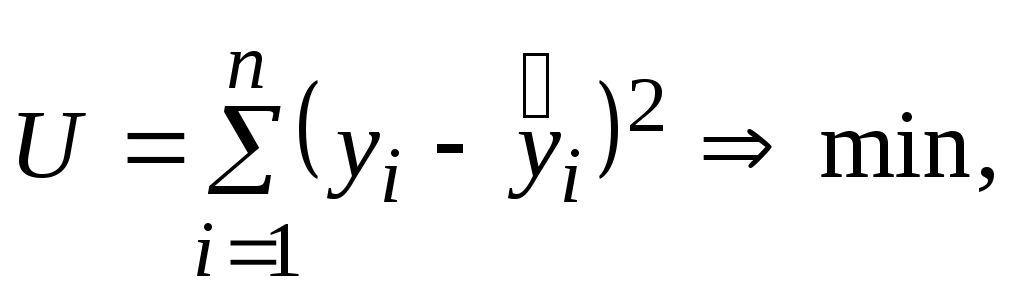 (5.2)
(5.2)
где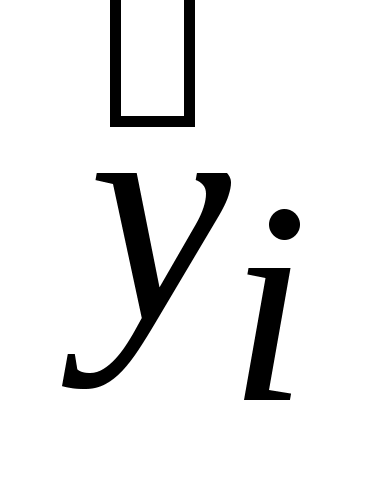 – значение y, рассчитанное по зависимости
– значение y, рассчитанное по зависимости 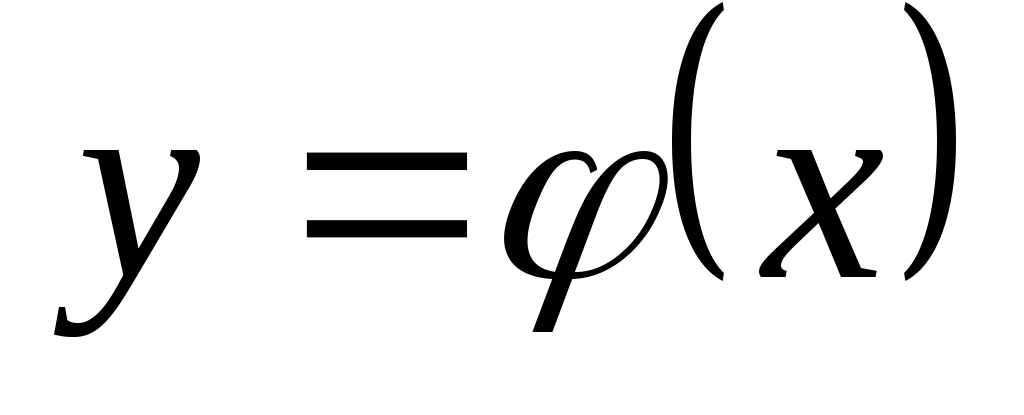 при x = xi.
при x = xi.
Следует заметить, что в данном случае величины xi и yi известны из опыта. При заданном виде функции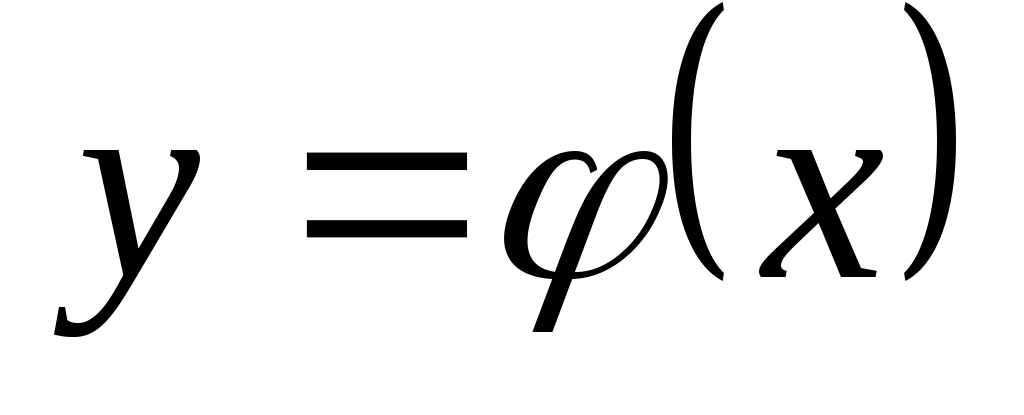 сумма квадратов отклонений результатов эксперимента от линии регрессии (величина U) является только функцией параметров a,b,c..., т.е. U = U(a,b,c,...).
сумма квадратов отклонений результатов эксперимента от линии регрессии (величина U) является только функцией параметров a,b,c..., т.е. U = U(a,b,c,...).
Необходимым условием минимума многопараметрической непрерывной функции на неограниченном диапазоне изменения параметров является равенство нулю частных производных по параметрам. Отсюда выполнение условия , представленного в виде
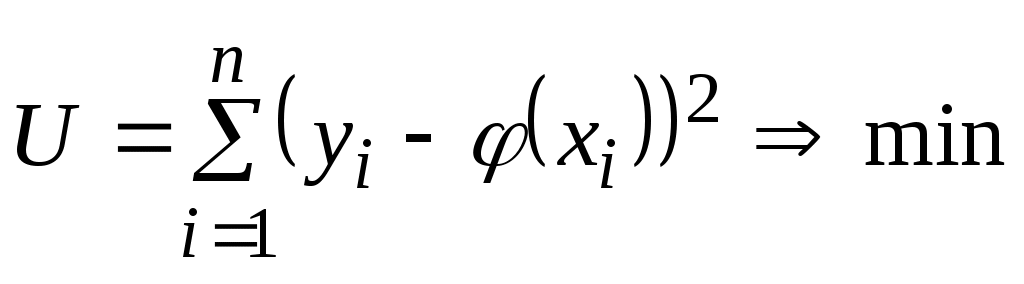 , (5.3)
, (5.3)
будет обеспечено при
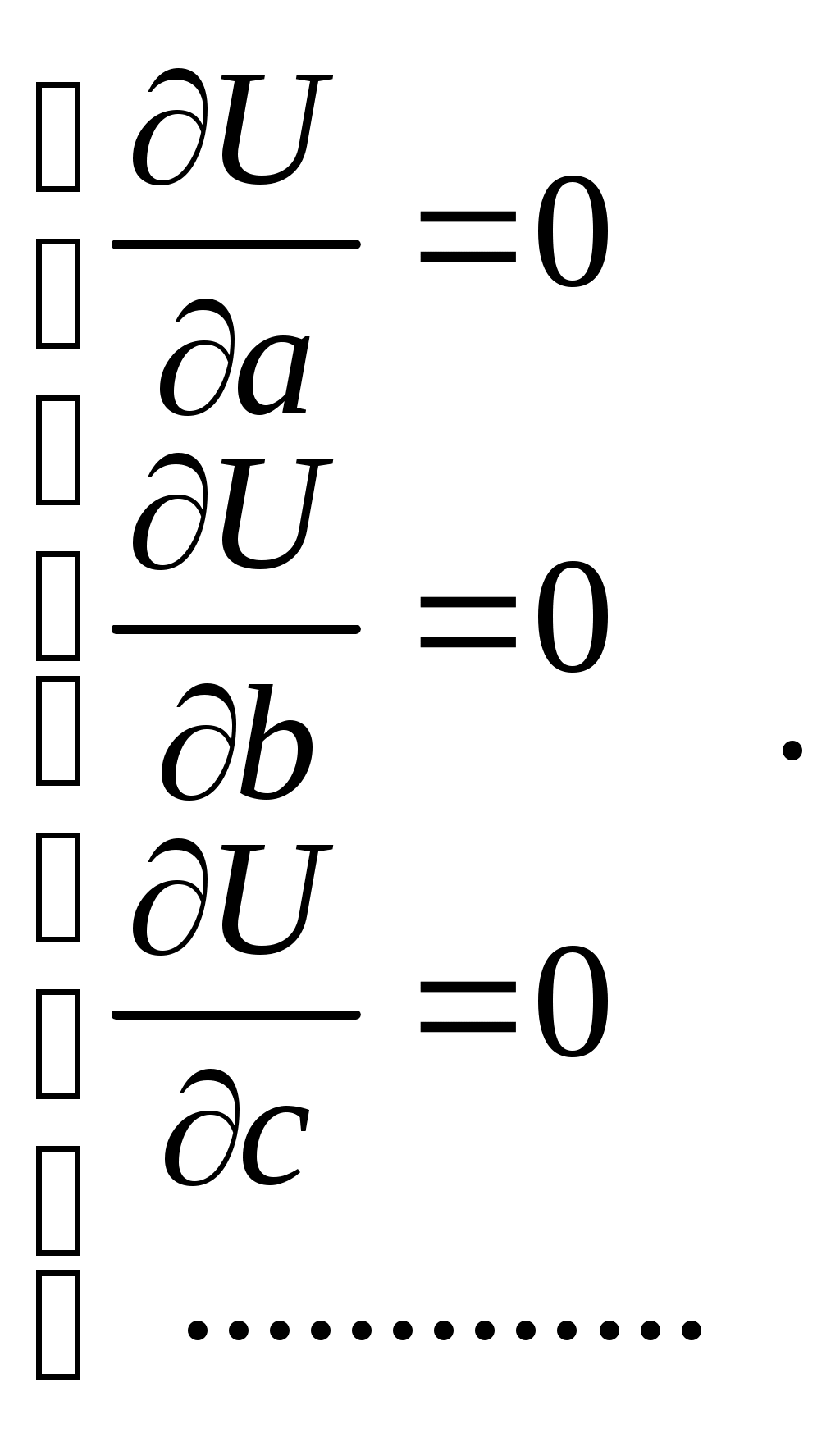 (5.4)
(5.4)
Количество уравнений в системе (5.4) равно количеству подлежащих определению параметров a, b, c,... Решая эту систему, можно найти значения параметров.
Еще раз отметим, что в общем виде эту систему решить нельзя, для этого необходимо задаться конкретным видом функции (x).
Наиболее часто в качестве уравнения регрессии используются алгебраические многочлены вида
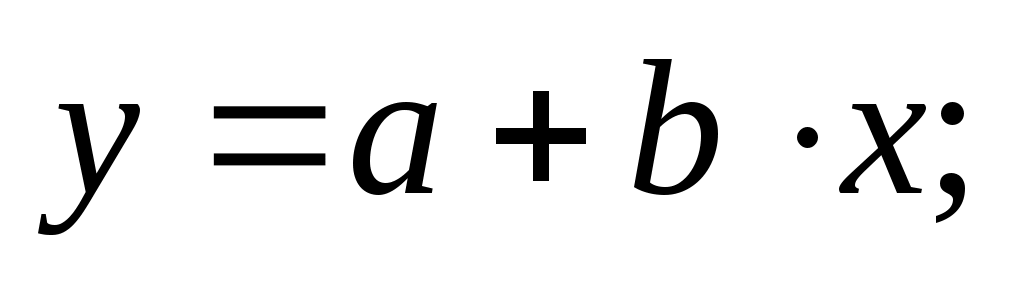
ё (5.5)
Подставляя (5.5) и (5.3) в (5.4), получим систему уравнений для определения неизвестных параметров a и b:
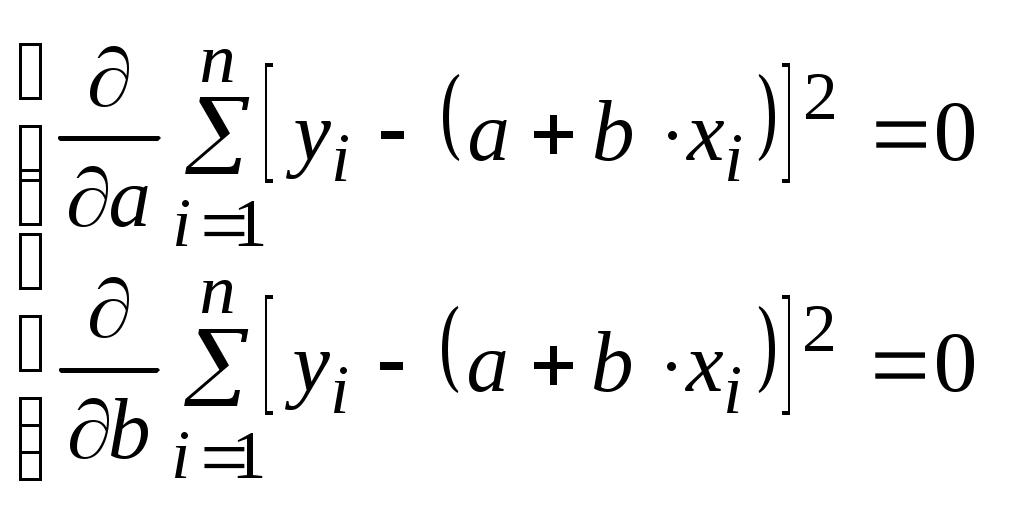 , (5.6)
, (5.6)
откуда, опуская индексы суммирования и проводя преобразования, получим систему из двух линейных уравнений:
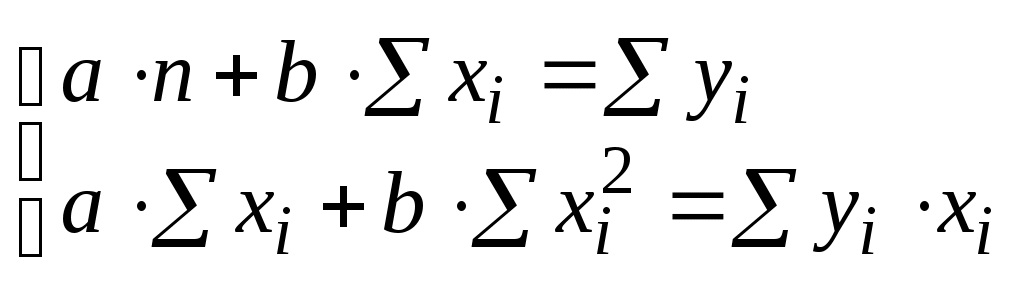 . (5.7)
. (5.7)
Решая систему (5.7) по правилу Крамера, получим
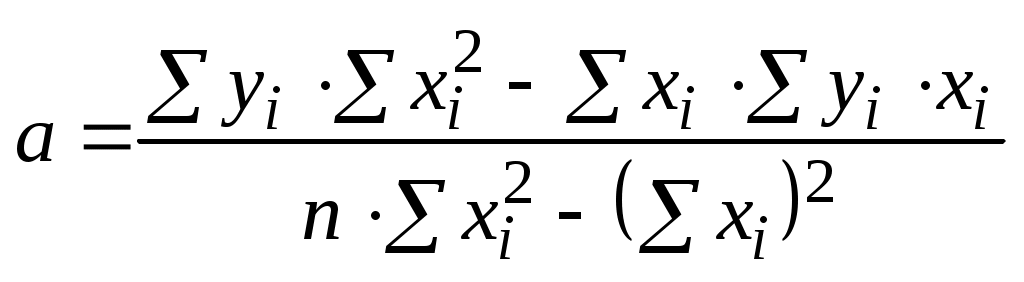 , (5.8)
, (5.8)
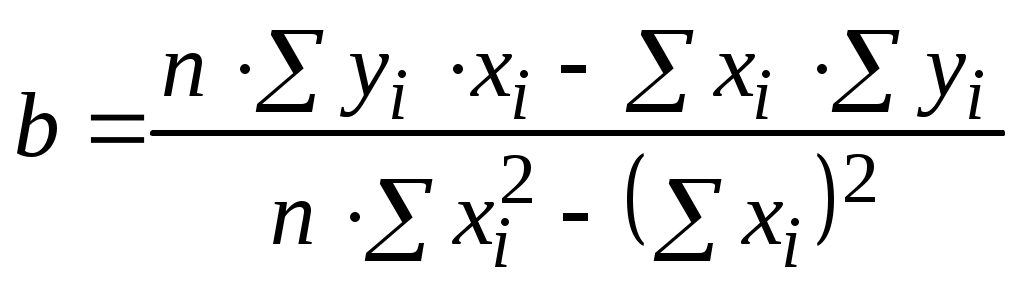 . (5.9)
. (5.9)
Вычисление коэффициентов по формулам (5.8) и (5.9) при ручной обработке экспериментальных данных целесообразно проводить в табличной форме (табл. 5.1).
Таблица 5.1 Методика первичной обработки результатов эксперимента
Для контроля правильности вычислений в табл. 5.1 используется выражение
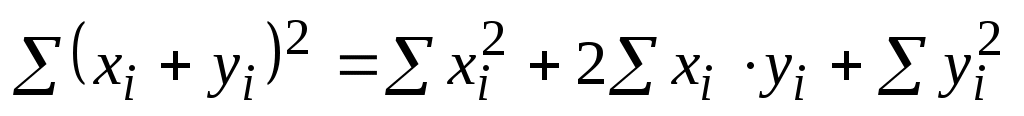 . (5.10)
. (5.10)
Разброс значений xi и yi относительно их средних значений определяется дисперсиями, которые рассчитываются по формулам:
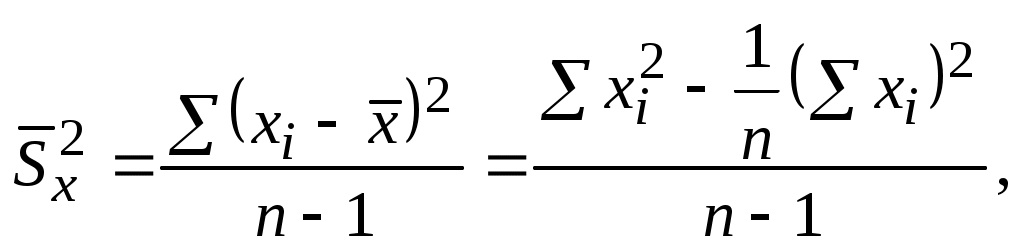 (5.11)
(5.11)
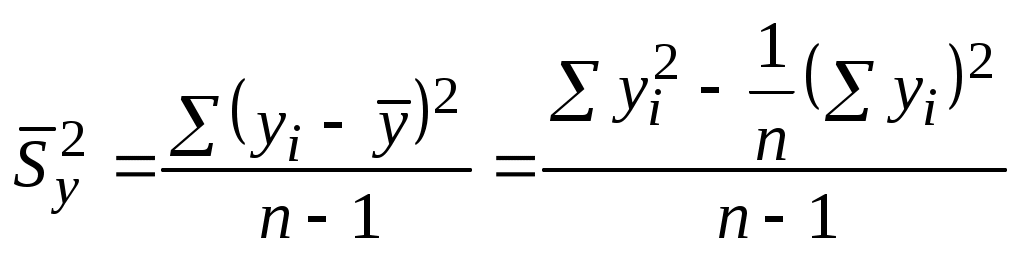 . (5.12)
. (5.12)
Качество аппроксимации оценивается по сумме квадратов отклонений экспериментальных значений yi от рассчитанных по (5.5)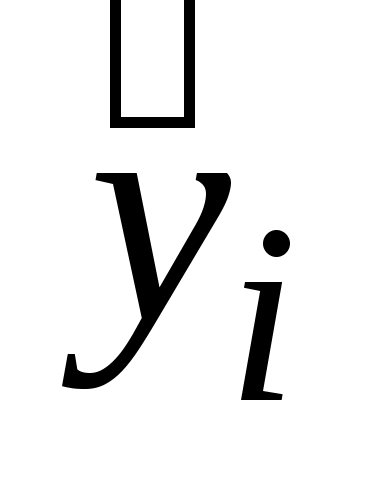 . Мерой расхождения служит остаточная дисперсия
. Мерой расхождения служит остаточная дисперсия
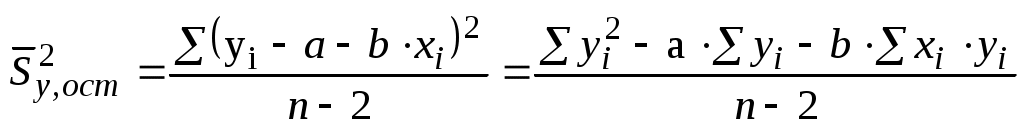 . (5.13)
. (5.13)
Адекватность описания результатов эксперимента уравнением регрессии проверяется по критерию Фишера:
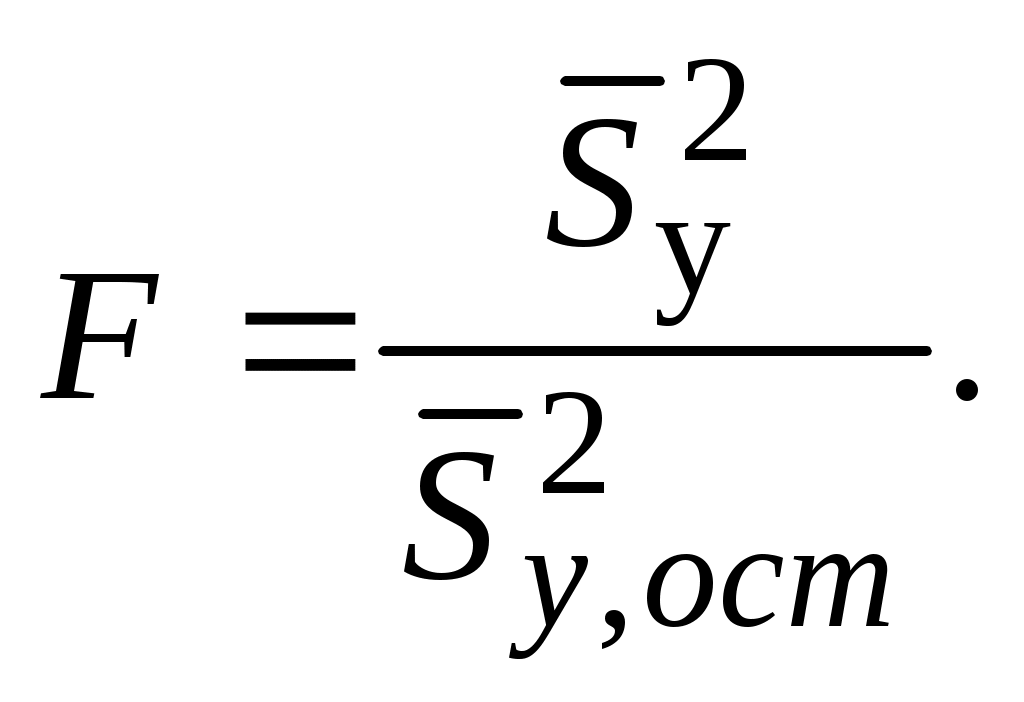 (5.14)
(5.14)
Полученное значение сравнивают с табличным Fкр,взятым из таблицы распределения Фишера по числу степеней свободы ν1 = n1-1,
ν2 = n2 - 1 и уровню значимости . При F > Fкр принимается, что уравнение регрессии соответствует результатам экспериментов, в противном случае уравнение регрессии признается неадекватным.
Представление результатов эксперимента уравнением (5.5) совершенно не означает, что между случайными величинами x и y действительно существует линейная зависимость. Для оценки меры линейной связи между двумя переменными используется коэффициент корреляции:
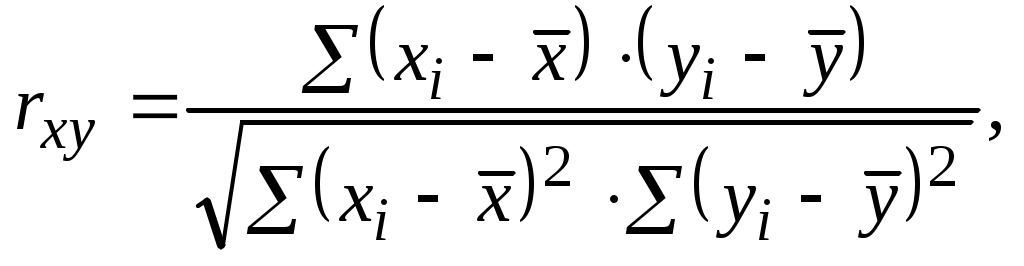 (5.15)
(5.15)
величина которого находится в пределах -1 rxy 1. Для вычисления более удобно представить выражение (5.15) в виде:
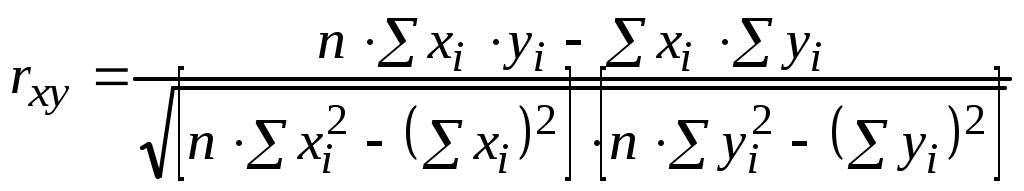 . (5.16)
. (5.16)
Знак коэффициента корреляции определяет направление изменения одной величины при изменении другой. При rxy > 0 увеличение значения x приводит в среднем к увеличению y, при rxy < 0 – к уменьшению y. Абсолютная величина rxy определяет тесноту линейной связи между x и y
. При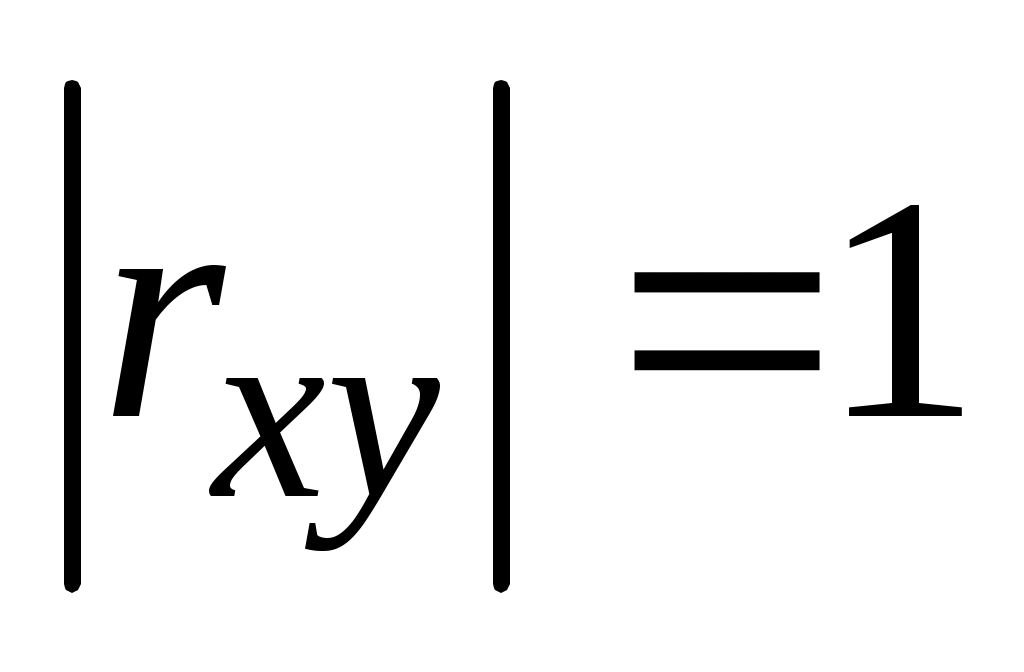 все значения y будут находиться на прямой, описываемой уравнением (5.5). При rxy=0 величины x и y линейно независимы.
все значения y будут находиться на прямой, описываемой уравнением (5.5). При rxy=0 величины x и y линейно независимы.
Поскольку значения величин x и y могут быть отягощены случайными погрешностями, то и параметры уравнения регрессии a и b, коэффициент регрессии rxy и значения , рассчитываемые по найденному уравнению регрессии, также представляют собой случайные величины.
, рассчитываемые по найденному уравнению регрессии, также представляют собой случайные величины.
Для того чтобы коэффициент корреляции rxy значимо отличался от нуля, необходимо выполнение условия:
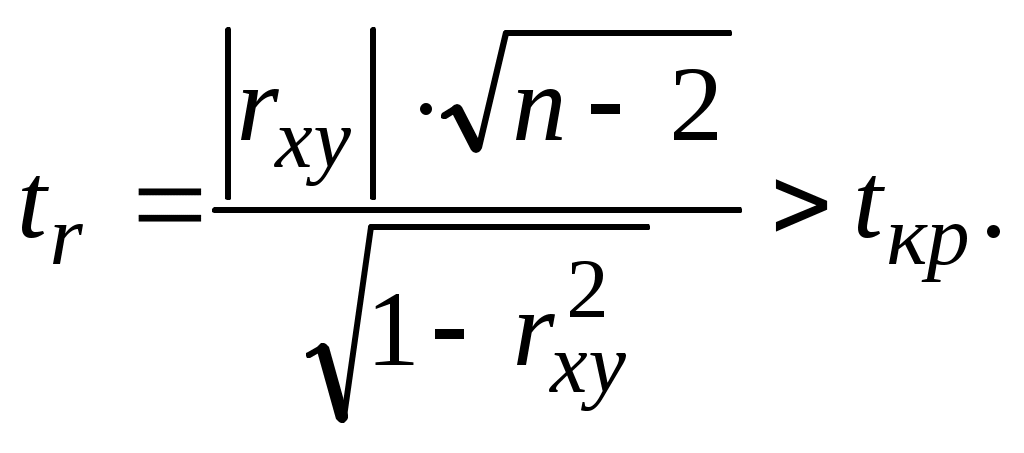 (5.17)
(5.17)
Параметр tкр определяется из таблицы t–распределения Стьюдента по числу степеней свободы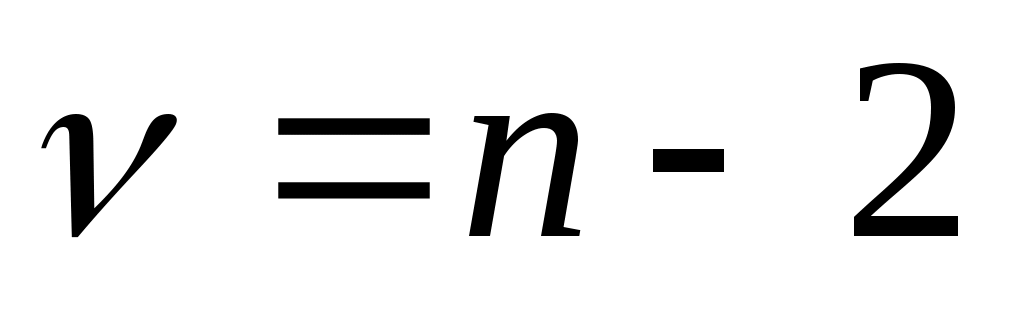 и выбранному уровню значимости .
и выбранному уровню значимости .
Доверительные интервалы, внутри которых с заданным уровнем значимости находятся истинные значения оцениваемых параметров, определяются выражениями:
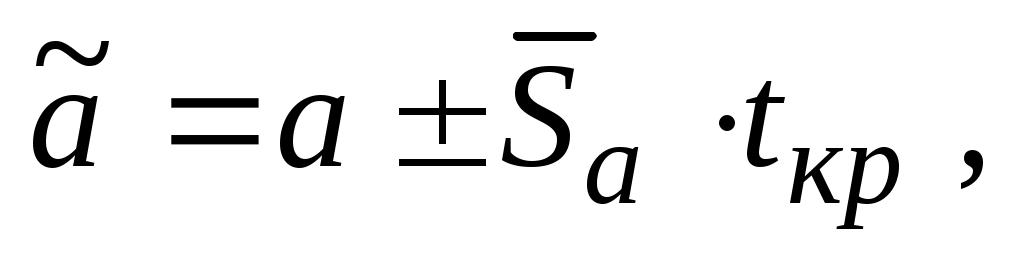 (5.18)
(5.18)
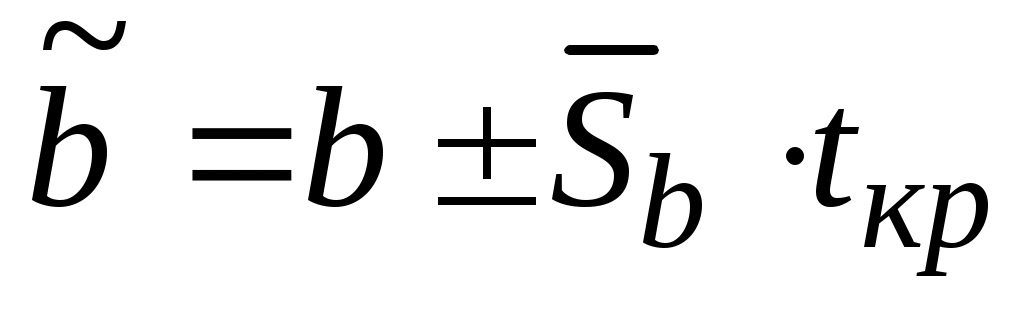 , (5.19)
, (5.19)
где средние квадратичные отклонения рассчитываются по формулам:
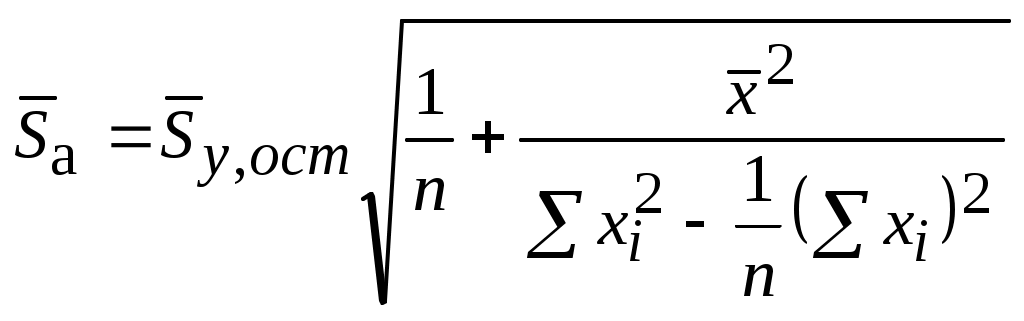 , (5.20)
, (5.20)
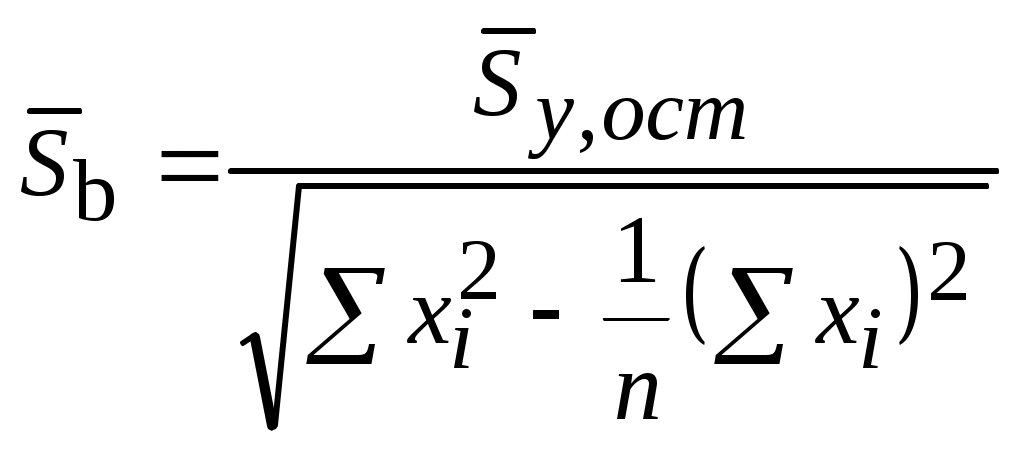 , (5.21)
, (5.21)
откуда доверительные интервалы линии регрессии составят
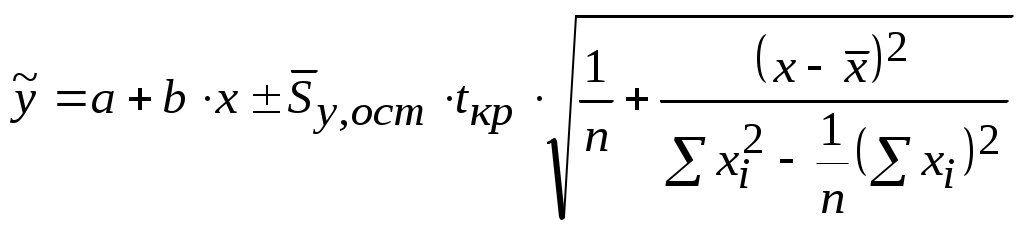 . (5.22)
. (5.22)
Задание на лабораторную работу
Для варианта исходных данных в табл. П 1.3:
– определить коэффициенты уравнения линейной регрессии;
– проверить адекватность регрессионного уравнения;
– определить коэффициент корреляции переменных х и у;
– оценить значимость коэффициента корреляции;
– найти доверительные интервалы коэффициентов и уравнения регрессии;
Затем в ячейку I20 запишем значение критерия Пирсона
χ2= 12,5960, найденное по табл. П 2.4 или с помощью функции ХИ2ОБР для = 0,05 и ν = 6.
Так как В < 2 = 12,6, то измерения признаются равноточными. Этот вывод записывается в ячейку А26.
Задание 3
Считаем, что во всех опытах проводилось по 4 опыта. Записываем в ячейку А28 заголовок Задание3. Далее определяем, что наибольший разброс данных (наибольшая дисперсия) наблюдался в первой серии опытов, копируем значение дисперсии
В ячейку В32 запишем значение Gкр=0,480, найденное по
табл. П 2.5 для = 0,05, ν = n–1 = 3 и k = 7.
Так как
Общий вид рабочего листа лабораторной работы №4 показан на рис. 4.1.

Рис. 4.1. Общий вид второй части лабораторной работы № 4
Лабораторная работа №5
Сглаживание результатов экспериментов
и построение парных линейных зависимостей
методом наименьших квадратов
Допустим, что для исследования взаимосвязи величин х и y были проведены n измерений и получен набор n пар значений xi и yi. Экспериментальные точки дают некоторый разброс относительно истинных значений, связанный с наличием случайных ошибок. При интерпретации этих данных необходимо ответить на следующие вопросы:
-
Можно ли с заданной вероятностью утверждать, что существует связь между величинами x и y? -
Если связь существует, то какой вид функции
описывает результаты эксперимента?
-
Какие численные значения коэффициентов a,b,c,... функции (x) обеспечивают наилучшее согласование экспериментальных и расчетных данных? -
Согласуется ли с результатами эксперимента (адекватно ли математическое описание результатов) выбранный вид функции (x) ? -
В каком диапазоне с заданной вероятностью находится математическое ожидание величины y(x)?
Экспериментальные данные желательно обработать так, чтобы по возможности точно отразить общую тенденцию зависимости y от x и вместе с тем сгладить отклонения, связанные с влиянием случайных неконтролируемых факторов. Задача сводится к выбору типа зависимости (5.1), чтобы эта зависимость в некотором смысле наилучшим образом отображала экспериментальные данные. Уравнение (5.1) называется уравнением регрессии, а параметры a, b, c … – коэффициентами регрессии.
Метод наименьших квадратов предполагает, что наилучшим приближением считается такое, при котором достигается минимум суммы квадратов отклонений расчетных и наблюдаемых значений y, то есть выполняется условие
где
Следует заметить, что в данном случае величины xi и yi известны из опыта. При заданном виде функции
Необходимым условием минимума многопараметрической непрерывной функции на неограниченном диапазоне изменения параметров является равенство нулю частных производных по параметрам. Отсюда выполнение условия , представленного в виде
будет обеспечено при
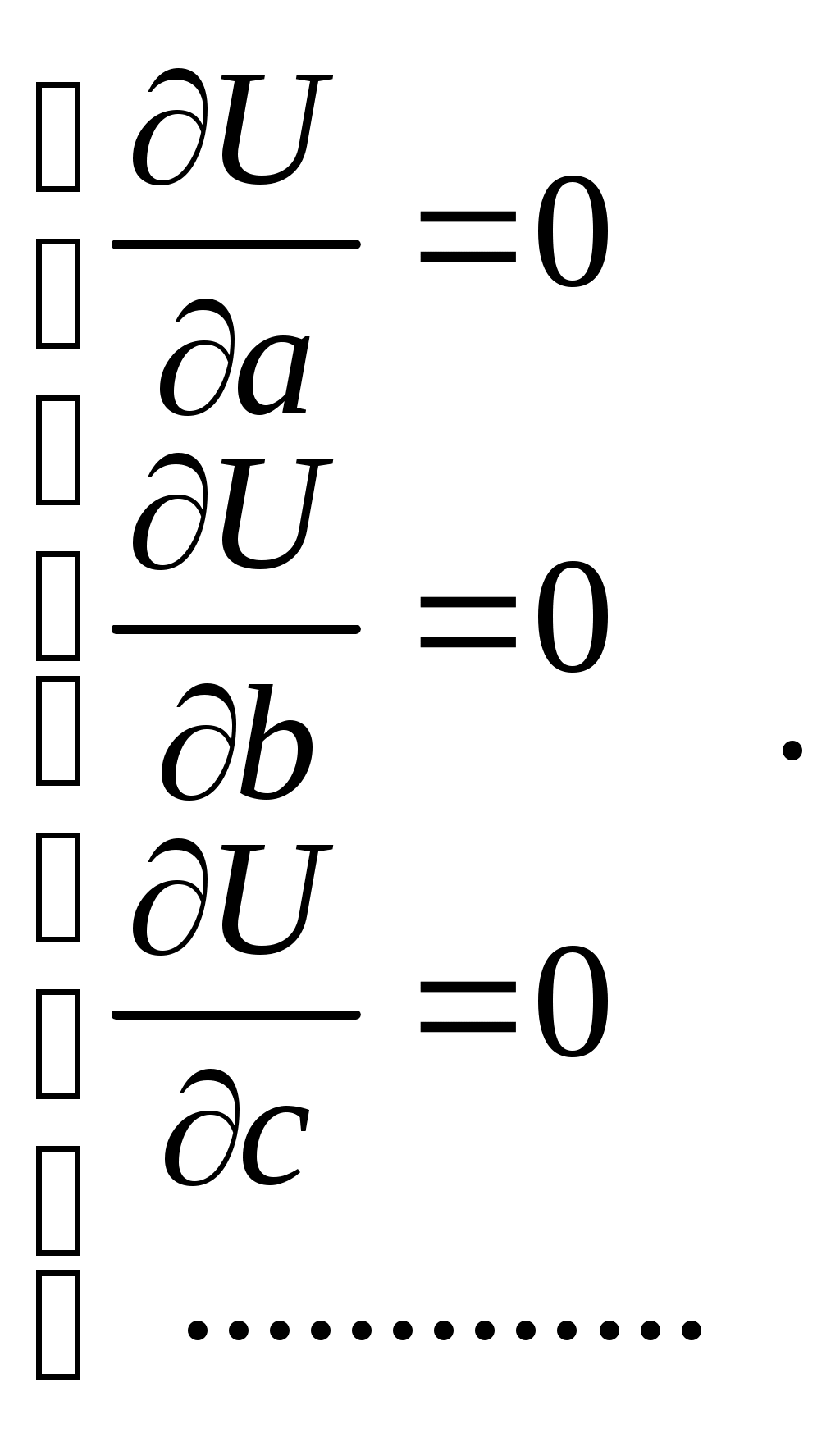 (5.4)
(5.4)Количество уравнений в системе (5.4) равно количеству подлежащих определению параметров a, b, c,... Решая эту систему, можно найти значения параметров.
Еще раз отметим, что в общем виде эту систему решить нельзя, для этого необходимо задаться конкретным видом функции (x).
Наиболее часто в качестве уравнения регрессии используются алгебраические многочлены вида
ё (5.5)
Подставляя (5.5) и (5.3) в (5.4), получим систему уравнений для определения неизвестных параметров a и b:
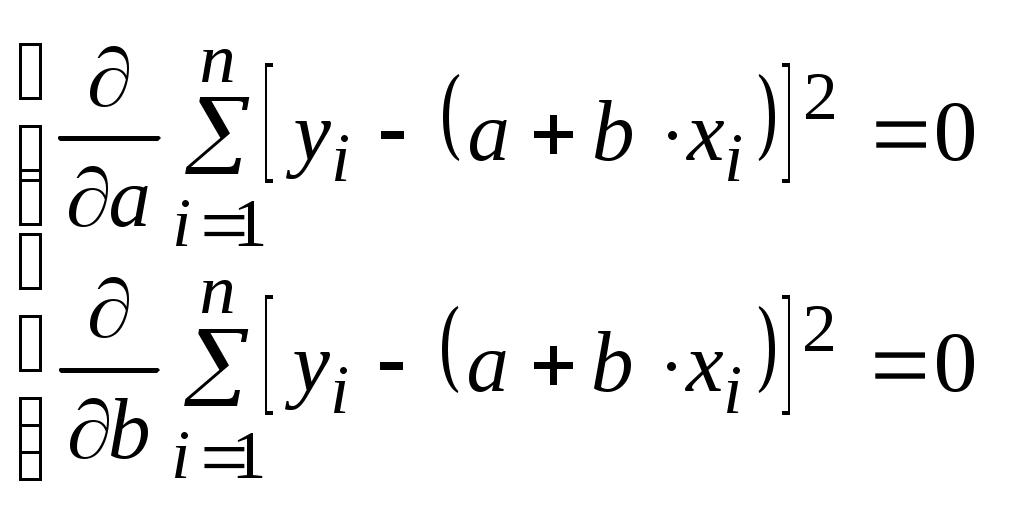 , (5.6)
, (5.6)откуда, опуская индексы суммирования и проводя преобразования, получим систему из двух линейных уравнений:
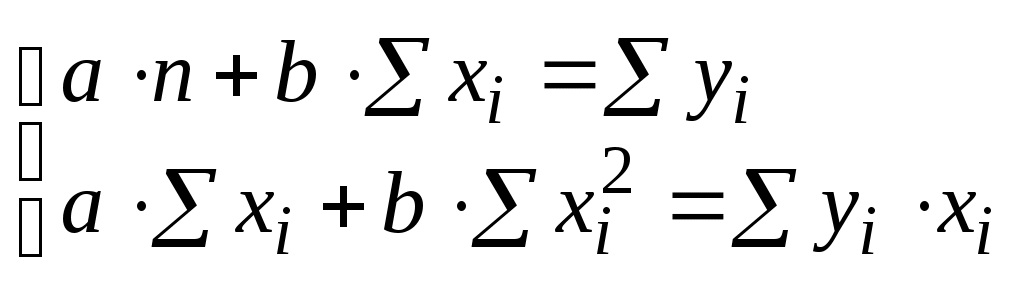 . (5.7)
. (5.7)Решая систему (5.7) по правилу Крамера, получим
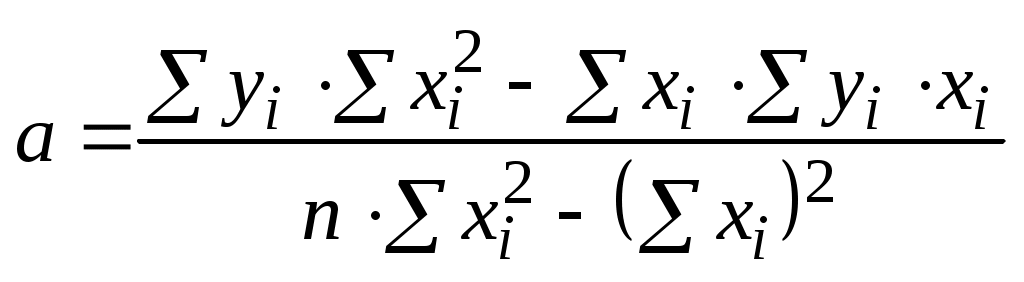 , (5.8)
, (5.8)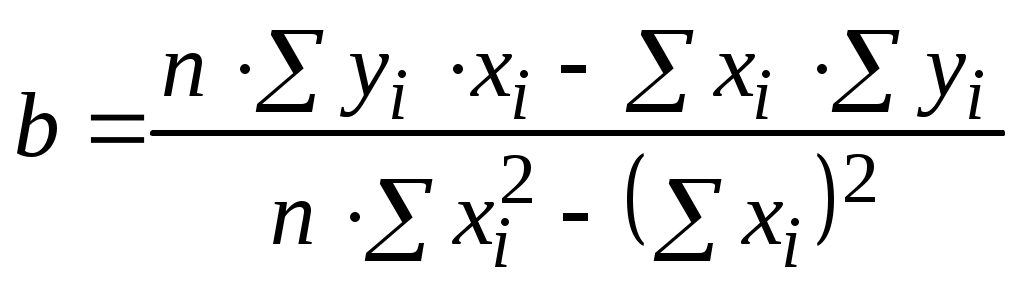 . (5.9)
. (5.9)Вычисление коэффициентов по формулам (5.8) и (5.9) при ручной обработке экспериментальных данных целесообразно проводить в табличной форме (табл. 5.1).
Таблица 5.1 Методика первичной обработки результатов эксперимента
| №№ опытов | x | y | x2 | y2 | xy | x+y | (x+y)2 |
| 1 | | | | | | | |
| 2 | | | | | | | |
| 3 | | | | | | | |
| … | | | | | | | |
| n | | | | | | | |
| | хi | yi | хi2 | yi2 | xiyi | (xi+yi) | (xi+yi)2 |
Для контроля правильности вычислений в табл. 5.1 используется выражение
Разброс значений xi и yi относительно их средних значений определяется дисперсиями, которые рассчитываются по формулам:
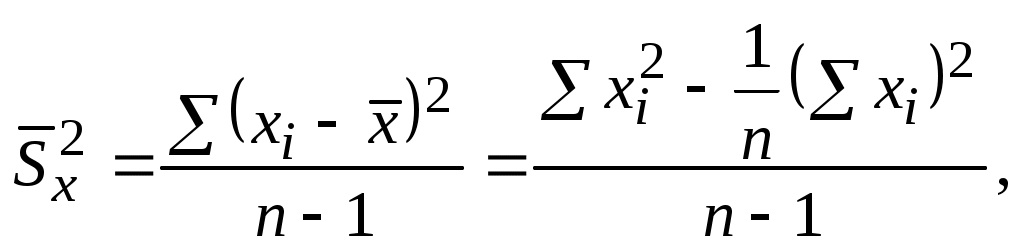 (5.11)
(5.11)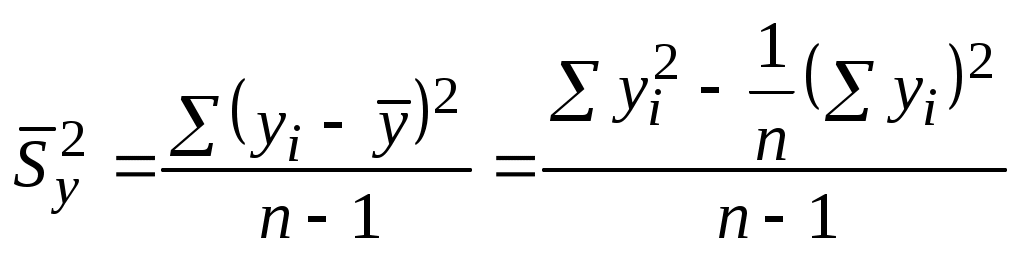 . (5.12)
. (5.12)Качество аппроксимации оценивается по сумме квадратов отклонений экспериментальных значений yi от рассчитанных по (5.5)
Адекватность описания результатов эксперимента уравнением регрессии проверяется по критерию Фишера:
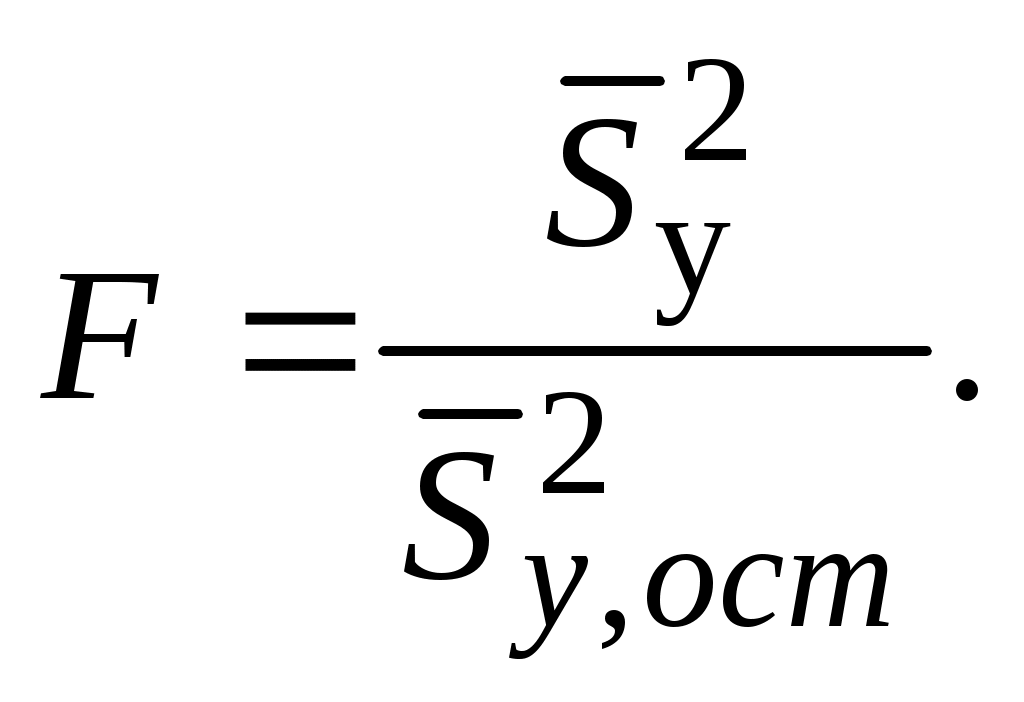 (5.14)
(5.14)Полученное значение сравнивают с табличным Fкр,взятым из таблицы распределения Фишера по числу степеней свободы ν1 = n1-1,
ν2 = n2 - 1 и уровню значимости . При F > Fкр принимается, что уравнение регрессии соответствует результатам экспериментов, в противном случае уравнение регрессии признается неадекватным.
Представление результатов эксперимента уравнением (5.5) совершенно не означает, что между случайными величинами x и y действительно существует линейная зависимость. Для оценки меры линейной связи между двумя переменными используется коэффициент корреляции:
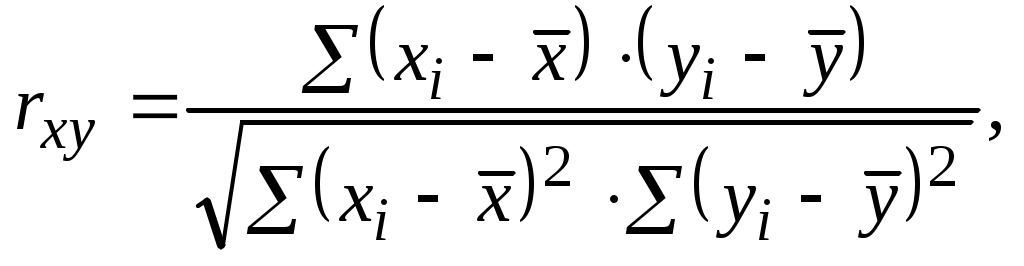 (5.15)
(5.15)величина которого находится в пределах -1 rxy 1. Для вычисления более удобно представить выражение (5.15) в виде:
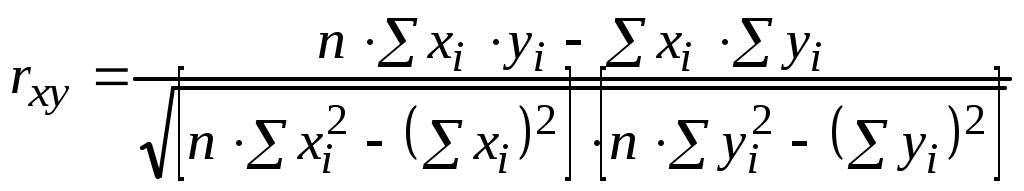 . (5.16)
. (5.16)Знак коэффициента корреляции определяет направление изменения одной величины при изменении другой. При rxy > 0 увеличение значения x приводит в среднем к увеличению y, при rxy < 0 – к уменьшению y. Абсолютная величина rxy определяет тесноту линейной связи между x и y
. При
Поскольку значения величин x и y могут быть отягощены случайными погрешностями, то и параметры уравнения регрессии a и b, коэффициент регрессии rxy и значения
Для того чтобы коэффициент корреляции rxy значимо отличался от нуля, необходимо выполнение условия:
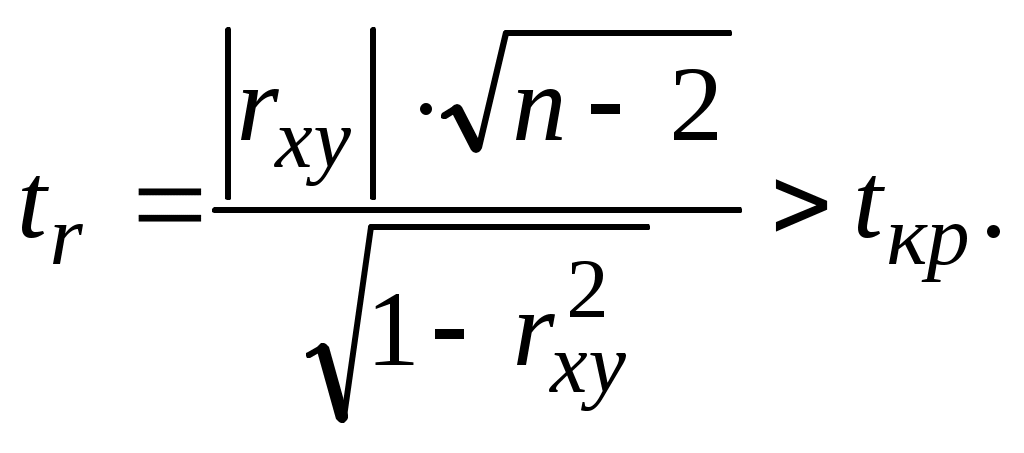 (5.17)
(5.17)Параметр tкр определяется из таблицы t–распределения Стьюдента по числу степеней свободы
Доверительные интервалы, внутри которых с заданным уровнем значимости находятся истинные значения оцениваемых параметров, определяются выражениями:
где средние квадратичные отклонения рассчитываются по формулам:
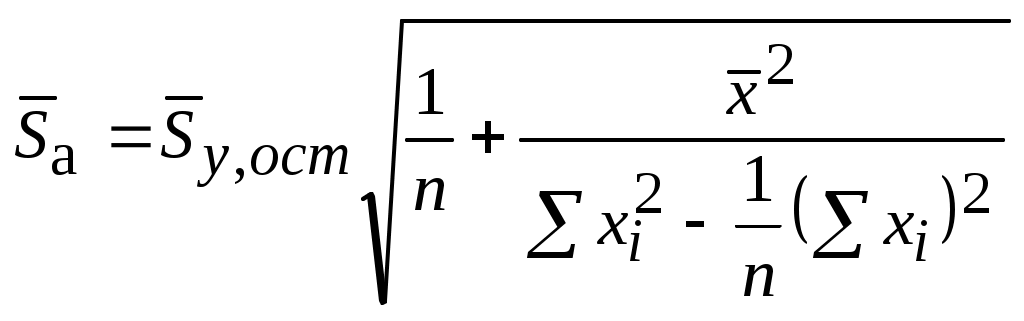 , (5.20)
, (5.20)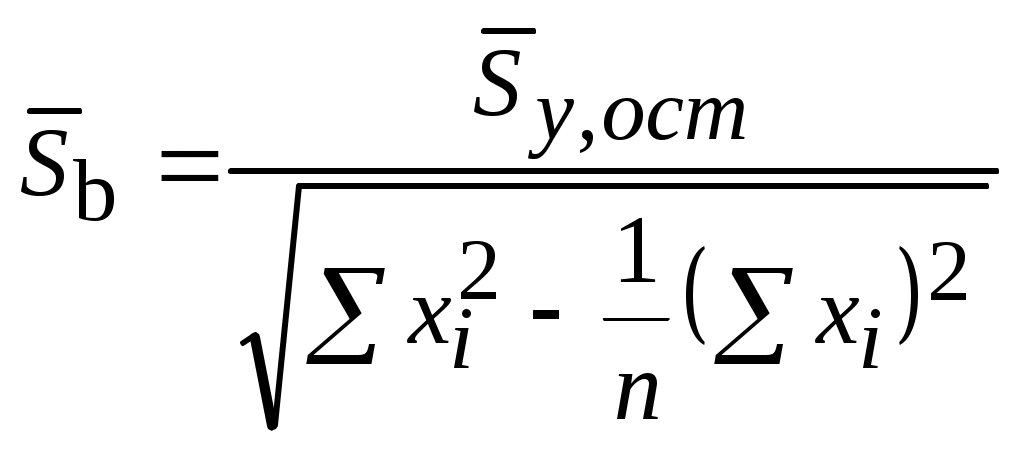 , (5.21)
, (5.21)откуда доверительные интервалы линии регрессии составят
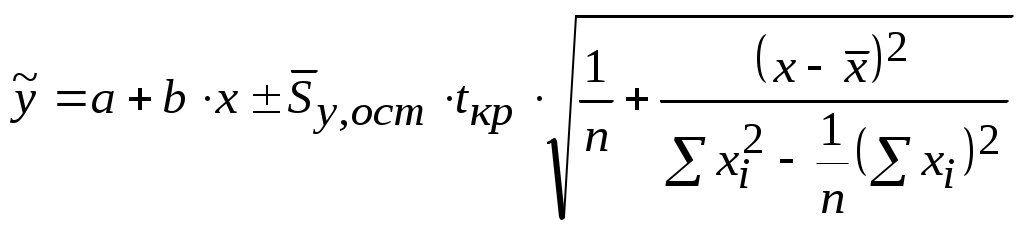 . (5.22)
. (5.22)Задание на лабораторную работу
Для варианта исходных данных в табл. П 1.3:
– определить коэффициенты уравнения линейной регрессии;
– проверить адекватность регрессионного уравнения;
– определить коэффициент корреляции переменных х и у;
– оценить значимость коэффициента корреляции;
– найти доверительные интервалы коэффициентов и уравнения регрессии;