Файл: Сборник методических пособий.doc

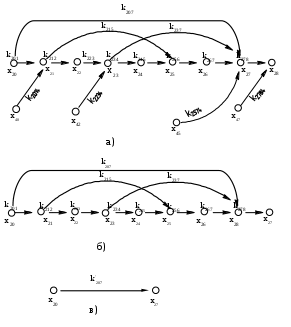
На рисунке 92, а представлен каскадный граф, показывающий в общем виде наследование отклонений формы поперечного сечения одной из деталей. В соответствии с изображением этого графа технологическое наследование отклонений формы представляется следующей системой уравнений:

;

;

;

;



Естественно, что вид графа, а следовательно, и соответствующая система уравнений целиком определяются принятым технологическим процессом со всеми его особенностями. Решение таких уравнений не составляет труда, необходимо сделать только ряд подстанов
ок. Значительно большие трудности возникают с получением соответствующей информации, т.е. с определением значений коэффициентов наследования.
Рисунок 92 – Каскадные графы
В общем виде отношения и взаимная зависимость свойств изделий на различных, в том числе и смежных, технологических операциях выражается уравнением . При этом характер наследования выражается через показатель степени h, a основные условия обработки определяются коэффициентом а. Последнее уравнение можно привести к линейному виду: .Величина характеризует значение наследуемого свойства после обработки; h·ln·x(i–1) – до обработки. Тогда логарифм показывает влияние метода обработки. Поэтому такое уравнение достаточно полно раскрывает механизм технологического наследования.

Коэффициент а, как коэффициент регрессии, может быть разложен в ряд Тейлора. Тогда в целом параметр наследуемого свойства после обработки раскладывается в следующий ряд:

и представляет собой некоторую поверхность в (j + 2)-мерном логарифмическом факторном пространстве. Коэффициенты регрессии в данном полиноме есть коэффициенты

---

Таким образом, дискретную наследственную связь можно описать уравнением где и — величины наследуемого свойства на входе и выходе наследственной связи; . — некоторые технологические факторы, присущие данной наследственной связи.

Каждую наследственную связь необходимо представить уравнениями указанного вида, а затем эти уравнения связать в систему. Тогда весь процесс технологического наследования некоторого свойства у опишем следующей системой:






. . . . . .


Далее необходимо решить задачу формирования массива технологических факторов таким образом, чтобы число разноименных технологических факторов, вносимых в систему, обеспечивало бы следующее равенство: , где – число наследственных связей, соответствующее числу уравнений в системе; – число анализируемых разноименных технологических факторов.

Становится очевидным, что рассматривать все технологические факторы в большинстве случаев не имеет смысла. Необходимо сосредоточить внимание на главных, определяющих факторах. Однако следует учитывать, что при исключении из анализа факторов, кажущихся второстепенными, четкость наследственных связей может нарушиться.

Наиболее целесообразно внести в массив все технологические факторы, полученные из производственного опыта, литературных источников, мнения специалистов-экспертов. Далее все факторы расставляют в порядке значимости и им присваивают необходимые номера. Соответствующая обработка массива позволяет облегчить решение ряда технологических задач, к которым относится: выбор оптимальных значений технологических факторов в соответствии с заданным изменением величины наследуемого свойства; прогнозирование параметров наследуемого свойства готовой детали по его значениям у заготовки; выбор заготовки; обеспечивающей заданное качество изделия.

---

Более простой случай технологического наследования погрешностей формы представлен на рисунке 93. Приведенному графу соответствует предыдущая система уравнений (1.1), в которой отсутствуют слагаемые, заключенные в квадратные скобки. Определенный интерес представляет нахождение значений в функции от . Для этого воспользуемся первыми (i+n) уравнениями. Простой граф, называемый приведенным, дающий в функции от , показан на рисунке 93, в. Искомая передача определяется методом подстановки:



о 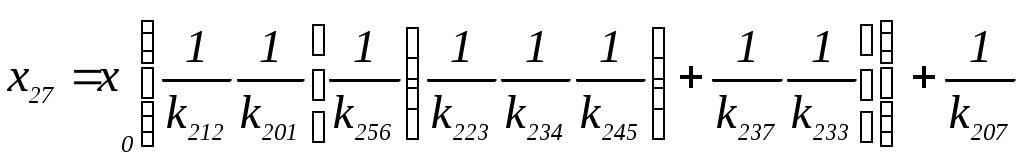ткуда передача приведенного графа



Очевидно, что при заданных значениях и можно найти передачу любой технологической операции, если известны передачи остальных операции.

В системе, имеющей обратную связь (рисунок 92), передачу можно найти на основе следующих рассуждений:



но Поэтому и передача оказывается равной

---

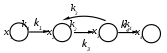
Рисунок 93 – Граф системы с обратной связью
Величина представляет собой коэффициент обратной связи, т.е. коэффициент, на который нужно умножить передачу, чтобы выявить полное влияние технологического процесса на формирование свойства. Выражение процесса технологического наследования с помощью системы уравнений облегчает задачу количественного определения свойств (значения х для многих случаев в литературе пока представлены недостаточно).

В сложном явлении наследования в ходе технологического процесса важнейшую роль играет передача и ее количественное значение. В одном случае на смежных операциях процесса значение передачи может быть таким, что свойство детали переносится полностью, либо даже становится более четко выраженным. Для другой пары смежных операций того же процесса передача оказывается едва заметной или отсутствует вовсе. В последнем случае очень важно установить ту точность, которой характеризуется наследственный перенос данного свойства. Например, часто принимают, что отдельные термические операции способны полностью устранить те напряжения, которые были получены ранее. Во многих случаях такое утверждение вполне допустимо. В действительности же после термической обработки напряжения в материале объекта производства могут остаться, хотя и весьма незначительные. Поэтому определить, произошел или нет наследственный перенос напряжений, можно установив, насколько существенно влияние оставшихся напряжений на выходной параметр детали.

Аналогичный подход следует применить и для оценки передаваемых отклонений формы деталей. Эти отклонения могут быть такими, что их, по малости, не принимают в расчет в одном случае, но считают большими — в другом. Однако, очевидно, малость таких отклонений не может явиться объяснением того, что процесс технологического наследования отсутствует. Аналогично, использование относительно грубых измерительных средств не дает основания утверждать, что определенный процесс или явление не имеют места, так как не регистрируются этими средствами.

В противовес детерминированным системам вероятностная модель содержит характеристики случайного изменения свойств обрабатываемой заготовки и характеристики рассеяния погрешностей ее обработки как внутри одной партии, так и в совокупности нескольких партий. Погрешности обработки на отдельно взятом переходе могут быть представлены в виде последовательности случайных величин

---

заданных функций распределения f ( ) = Р ( < ), где – некоторое предельное значение а.

Во многих случаях представление механизма технологическо­го наследования становится более удобным с помощью системы уравнений. Это тем более оправданно, что можно использовать ЭВМ, полагая, что число параметров, участвующих в процессе технологического наследования, оказывается во многих случаях очень большим.

---