Файл: Бодалев А. А. Столин В. В.docx

Рис. 16. Зависимость вероятности критериального события р и диагностических параметров X₁ и Х₂

С точки зрения распознавания образов, предварительная задача диагностики (предваряющая практические задачи) – определить границы диагностических категорий - областей в пространстве параметров, которым эмпирически корректно могут быть приписаны некоторые пороговые (качественно специфичные) значения прогнозируемого критериального показателя. Это задача построения «разделяющего правила» (или «решающего правила»). Точность такого разделения и предопределяет прогностическую валидность методики на данной совокупности испытуемых в данной диагностической ситуации.

Репрезентативность выборки при этом определяется степенью изменения точности разделения при увеличении совокупности обследованных. Влияние того или иного параметра на точность разделения определяет «вес», с которым входит данный параметр в задачу диагностики.

Построение формальной процедуры разделения может производиться по-разному. В простейшем случае - это сравнение тестового показателя с некоторым порогом. В более сложных случаях применяются методы дискриминантного анализа, позволяющие описывать «разделяющие правила» (границы диагностических областей в пространстве параметров) в виде сложных функций сразу от нескольких параметров.

Применение определенного метода для решения задачи построения системы диагностических категорий определяется несколькими факторами: во-первых, это соответствие допущений, положенных в основу алгоритма, содержательным представлениям о психологической типологии индивидов в рамках рассматриваемой системы психодиагностических параметров; во-вторых, это степень полноты имеющейся информации для эффективной «остановки» алгоритма, обеспечивающей оптимальное решение задачи за приемлемое время.

Под полнотой информации здесь, имеется в виду наличие достаточно многочисленных групп индивидов, четко и однозначно классифицированных по заданной системе критериев. В этом случае построение решающего правила сводится к применению какого-либо алгоритма автоматической классификации, приспособленного к работе с заданными классами. Если же критериальные классы представлены неполно - всего несколькими представителями, для которых при этом не всегда

---

известны все значения необходимых параметров, - то возникает ситуация, требующая применения так называемых эвристических алгоритмов (более подробно о применяемых алгоритмах классификации см. кн.: Типология и классификация в социологических исследованиях. М., 1982).

Остановимся на одном из методов распознавания, получившем применение в психодиагностике, — на семействе алгоритмов вычисления оценок (АВО), предложенном Ю. И. Журавлевым и его учениками (1978).

Основную задачу распознавания образов можно сформулировать как задачу отнесения объекта 5 к одному или нескольким классам К₁ К₂,..., К_i на основе информации о классах I (K₁), (К₂),..., I (К_i), информации об объекте I(S) и предположения о близости объекта к классу. Другими словами, задачу распознавания можно сформулировать как задачу определения того, обладает ли объект определенными свойствами.

В основе АВО лежит принцип частичной прецедентности: близость объекта к классу тем больше, чем больше частей в его описании «похожи» на соответствующие части в описаниях' объектов, чья принадлежность классу известна. Например, в одном из вариантов АВО (Зеличенко А. И., 1982) функция близости объекта S к классу К определяется так:

n m

Г(S,K)  P_jB(a _j (S_i^K )), (3.5.3)

i1 j1



^K 1,еслиa

B(a j (S),a j (Si _{)) }^j (SⁱK₎^j

_0 - в противном случе

где S_i^K - i-й объект, принадлежность которого к классу К уже известна; a_i (S) - i-й элемент (параметр) в описании объекта; P₁ - его вес; ε_j - i-й порог.

После того как вычислены Г(S₁ K₁,), ... , Г(S₁ K₁,) на основании некоторого решающего правила (зависящего от вектора параметров



B , принимается решение о принадлежности объекта к одному или нескольким классам К₁, ..., К₁ В задачах психодиагностики S- это испытуемый.

---

Таким образом, каждый вариант АВО определяется набором значений параметров. В нашем случае- это векторы p (p1  p_m),

 (1,...,_m) . Если информация об объекте S представлена в виде I(S)

= (а_1,..., а₂), то элемент вектора опорных множеств ω_j(S) = а_i, a ε_j -j-й порог.

В качестве примера решающего правила можно привести следующее (линейное пороговое решающее правило):

объект S принадлежит к классу K_t если

i

b_i^t Г(S,K_i )  C₁^t (3.5.4) j1

объект S не принадлежит к классу K_t если i

b_i^t Г(S,K_i )  C₂^t (3.5.5) j1

в остальных случаях -отказ от распознавания принадлежности

объекта S к классу K_t.

В работе алгоритмов распознавания вообще и АВО в частности можно выделить два этапа: обучение и собственно распознавание. На этапе обучения, как уже говорилось, происходит настройка алгоритма, т. е. выбор таких его параметров, которые обеспечивают оптимальное в нег котором смысле распознавание объектов обучающей выборки (объектов, принадлежность которых к классам К₁, ... ,K_i, известна). На этапе собственно распознавания происходит отнесение к классам K₁,..., К_i, тех объектов, принадлежность которых к классам априорно неизвестна.

Точность распознавания на этапе обучения измеряется полнотой и адекватностью распознавания эталонных объектов. Наряду с понятием «точность» (абсолютная отделимость) иногда удобно использовать понятие относительной отделимости объектов обучающей выборки, принадлежащих к различным классам. В случае, когда распознавание ведется для двух классов (например, в профориентации - для дифференциального прогноза успешности оптанта в одной из двух профессиональных областей), относительную отделимость можно определить как

X  X

^min (3.5.6)

100  X

min

где X - точность при обучении (выраженная в процентах), a

X -минимальная возможная точность обучения (совпадает с долей min

объектов в наибольшем классе от общего объема обучающей выборки). На этапе собственно распознавания точность характеризует главным образом репрезентативность обучающей выборки (выборки валидизации). Чем выше репрезентативность

---

, тем больше совпадают показателе точности на этапах обучения и собственно распознавания.

Использование АВО кроме решения задачи распознавания позволяет получить следующую информацию:

1. 
   Информационные веса отдельных элементов (параметров) описания объектов. Эти веса измеряются через изменение точности распознавания при исключении соответствующих параметров из описания эталонных объектов:
   

 (a _j )  ( (a _j ))a (3.5.7)



где X - точность распознавания при Р_j = 1; X(a_j ) - точность распознавания при Р. = 0, а а - нормирующий множитель. Информационные веса интерпретируются как мера прогностической важности параметров.

2. 
   Оптимальные значения порогов  , т. е. значения  , обеспечивающие наивысшую точность распознавания. Эти значения порогов в нашем случае можно .интерпретировать как чувствительность методики; ε_j - своего рода дифференциальный порог на шкале тестового показателя a_j определяющий переход индивида из одной диагностической категории в другую. Пусть на этапе разработки теста (тестовой батареи) была обследована группа из К человек, про которых известно, что K₁ из них относится к одному классу, а К₂ - к другому, К = К₁ + К₂. Выбрав случайным образом из этой группы М (М<<К) многомерных описаний, проводим на них процедуру обучения алгоритма. Точность обучения характеризует валидность теста. После этого применяем процедуру собственно распознавания (по выработанному решающему правилу) для остальных К-М описаний. В результате этой процедуры мы определяем принадлежность респондентов (испытуемых) к этим классам. Сравнивая полученные результаты с эталонными данными о принадлежности испытуемых к классам, мы определяем точность самого распознавания. Если эта точность близка к точности обучения, то наша пилотажная выборка объемом М может быть признана репрезентативной для обучения. Теперь можно переходить к задаче определения информационных весов.
   

---

* * *

Для эффективного использования алгоритмов распознавания по отношению к многомерным тестовым системам (при K>3), как правило, требуется использование компьютера.

При решении задач небольших размерностей (по количеству параметров) иногда психолог может быстрее найти решающее правило, применяя собственные способности зрительной системы (очень мощные) к визуально-геометрической группировке объектов. В пространстве параметров диагностические, классы выглядят как «сгущения», некие «облака» из точек, изображающих испытуемых. В этом случае при наличии априорной информации о принадлежности индивидов к классам удобно изображать точки из различных классов разными цветами (хуже - квадратиками, кружками, треугольниками). В этом случае «решающее правило» легко «увидеть» как некую воображаемую линию (прямую или кривую), разделяющую точки разного цвета (рис. 17). Точность диагностики в данном случае можно оценить по количеству точек, попавших при данном решающем правиле в «чужую» половину пространства параметров.



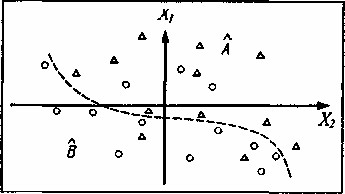
Рис.17. Разделение двух классов объектов (изображены кружками и треугольниками) в пространстве двух параметров

X₁, и Х₂

Точность правила, изображенного на рис. 17, равна:



А В

	10	2
3		12

A

B

  0,63

Здесь в четырехклеточной матрице сопряженности по строкам задано попадание объекта в один из априорных классов А (треугольники на рис. 17) или В (кружочки на рис. 17), а по столбцам - попадание объектов в один из апостериорных классов, образованных приме-



нением решающего правила, - А (слева от критериальной линии) или

---