ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.11.2023
Просмотров: 934
Скачиваний: 3
СОДЕРЖАНИЕ
1.3. ПСИХОДИАГНОСТИЧЕСКИЕ ЗАДАЧИ
1.4. ДИФФЕРЕНЦИАЛЬНАЯ ПСИХОМЕТРИКА
1.5. НОРМАТИВНЫЕ ПРЕДПИСАНИЯ РАЗРАБОТЧИКАМ И ПОЛЬЗОВАТЕЛЯМ ПСИХОДИАГНОСТИЧЕСКИХ МЕТОДИК
1.5.2. Требования к пользователям
1.5.3. Использование методик специалистамисмежниками
ГЛАВА 2 ИЗ ИСТОРИИ ПСИХОДИАГНОСТИКИ
2.1. ИЗ ИСТОРИИ ПСИХОЛОГИЧЕСКИХ ТЕСТОВ
2.2. ИЗ ИСТОРИИ ПРОЕКТИВНОГО МЕТОДА
Классификация видов проекции по Холмсу
2.3. ИЗ ИСТОРИИ КОНТЕНТ-АНАЛИЗА КАК ПСИХОДИАГНОСТИЧЕСКОЙ ПРОЦЕДУРЫ
3.1. РЕПРЕЗЕНТАТИВНОСТЬ ТЕСТОВЫХ НОРМ
Рис. 1.Соотношение индивидуальной и общей вариации тестовых баллов
3.4. ТЕХНОЛОГИЯ СОЗДАНИЯ И АДАПТАЦИИ МЕТОДИК
3.5. ПРОГНОЗИРОВАНИЕ И РАСПОЗНАВАНИЕ ОБРАЗОВ
Рис. 16. Зависимость вероятности критериального события р и диагностических параметров X1 и Х2
3.6. ТРЕБОВАНИЯ К ПСИХОМЕТРИЧЕСКОЙ ПОДГОТОВКЕ ПСИХОЛОГА
ГЛАВА 4 ПСИХОДИАГНОСТИКА ЧЕРТ ЛИЧНОСТИ
Рис. 18. Концептуальный куб, иллюстрирующий континуальную модель черты личности
Рис. 21. «Четырехполюсное» описание черт «экстраверсия-нтроверсия» при ортогональных параметрах
Рис. 28. Образец задания из субтеста «Абстрактное мышление» (DAT)
Рис. 29 Образец задания из субтеста «Пространственные отношения» (DAT)
Рис. 30. Образец задания из субтеста «Техническое мышление» (DAT)
5.4. ОБЛАСТИ ПРИМЕНЕНИЯ ТЕСТОВ СПОСОБНОСТЕЙ
6.2. ИЗМЕРЕНИЕ МОТИВАЦИИ ДОСТИЖЕНИЯ
Рис. 31. Зависимость Та от силы мотивов Мs и MAf и от субъективной вероятности успеха Ps
6.3. ОПРОСНИК ДЛЯ ИЗМЕРЕНИЯ ПОТРЕБНОСТИ В ДОСТИЖЕНИИ
Таблица 9 Результаты кроссвалидизации тест-опросника
Образец матрицы поведения ребенка
Матрица игры «Дилеммы узников» Выбор игрока Б
7.2. СОВМЕСТНЫЙ ТЕСТ РОРШАХА ДЛЯ ДИАГНОСТИКИ НАРУШЕНИЙ СЕМЕЙНОГО ОБЩЕНИЯ
Обработка данных СТР (на поведенческом уровне)
ГЛАВА 8 ПСИХОДИАГНОСТИКА ИНДИВИДУАЛЬНОГО СОЗНАНИЯ
Рис. 32. Способ последовательного вызывания конструктов и элементов
Рис. 35. Монолитная —(а), артикулированная - (б) и фрагментарная - (в) системы конструктов
ГЛАВА 9 ПСИХОДИАГНОСТИКА САМОСОЗНАНИЯ
9.2. МЕТОДИКИ ПСИХОДИАГНОСТИКИ САМОСОЗНАНИЯ
9.4. МЕТОДИКА УПРАВЛЯЕМОЙ ПРОЕКЦИИ
9.6. МЕТОДИКА КОСВЕННОГО ИЗМЕРЕНИЯ СИСТЕМЫ САМООЦЕНОК (КИСС)
Рис. 37. Параметры методики КИСС
Рис. 38. Графическое изображение индивидуальной обработки КИСС
Очевидно, что дифференцирующая способность теста сводится к нулю, если кривые, иллюстрирующие «истинную» и «ошибочную» дисперсии» совпадают. Как видим, анализ распределения тестовых баллов необходим уже для анализа надежности теста (см. раздел 3.2).
Проблема меры в психометрике и свойства пунктов теста. В физических измерениях калибровка шкалы производится на основе контроля за равномерным варьированием измеряемого свойства в эталонных объектах. Носителем меры является эталон- физический объект, стабильно сохраняющий заданную величину измеряемого свойства. В дифференциальной психометрике такие физические эталоны отсутствуют: мы не располагаем индивидами, которые были бы постоянными носителями заданной величины измеряемого свойства.
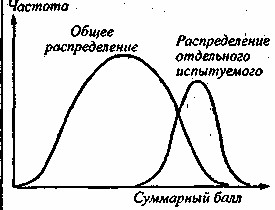
Рис. 1.Соотношение индивидуальной и общей вариации тестовых баллов
Роль косвенных эталонов в психометрике выполняют сами тесты: в том смысле, в каком трудность задач можно рассматривать как величину, прямо пропорционально сопряженную со способностью (чем труднее задача, тем выше должен быть уровень способности, требуемый для ее решения). Аналогом понятия «трудность» для «ливопросов»6 опросника является «сила»: более «сильные» высказывания (в логическом смысле) вызывают подтверждение (согласие) у меньшего числа испытуемых. Ни трудность, ни силу пунктов теста нельзя выявить иначе, чем с помощью проведения теста. Операциональным определением трудности оказывается «процентильная мера»: процент испытуемых, справившихся с заданием теста (или ответивших «верно» на «ли-вопрос»). Чем меньше процент, тем выше трудность.
Кривая распределения тестовых баллов отражает свойства пунктов, из которых составлен тест. Если кривая имеет правостороннюю асимметрию, то в тесте преобладают трудные задания; если кривая имеет левостороннюю асимметрию, значит, большинство пунктов в тесте - легкие (слабые) (рис. 2).
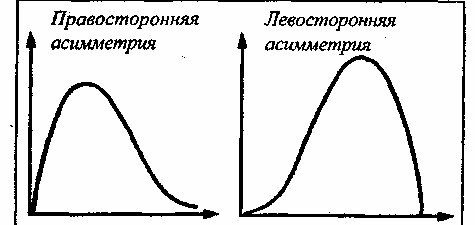
Рис. 2.Асимметрии распределения тестовых баллов
Тесты первого типа плохо дифференцируют испытуемых с низким уровнем способностей: все эти испытуемые получают примерно одинаковый низкий балл. Тесты второго типа, наоборот, хуже дифференцируют испытуемых с высоким уровнем способностей.
Если пункты обладают оптимальным уровнем трудности (силы), то кривая распределения зависит от того, насколько пункты однородны. Если пункты разнородны (исход по одному пункту не предопределяет исход по другому), то мы получаем тест в виде последовательности независимых испытаний Бернулли. Как известно из математической статистики, при достаточно большом количестве независимых испытаний с двумя разновероятными исходами кривая биномиального распределения (кривая суммарного балла) по закону больших чисел автоматически приближается к кривой нормального распределения (центральная предельная теорема Муавра - Лапласа). Если тест содержит разнородные задания примерно равного уровня трудности (именно такие задания и подбираются для измерения интегральных свойств личности), то нормальность распределения суммарных баллов возникает автоматически - как артефакт самой процедуры подсчета суммарных баллов. При этом, конечно, форма кривой распределения баллов не позволяет говорить о реальной форме распределения измеряемого свойства, каким оно является само по себе - в широкой популяции испытуемых. Нормальность распределения есть артефакт, прямое следствие направленного отбора пунктов с заданными свойствами.
Если подбираются пункты, тесно положительно коррелирующие между собой (испытания не являются статистически независимыми), то в распределении баллов возникает отрицательный эксцесс (рис. 3,а), Максимальных значений отрицательный эксцесс достигает по мере возрастания вогнутости вершины распределения - до образования двух вершин -двух мод (с «провалом» между ними -рис. 3,6). Бимодальная конфигурация распределения баллов указывает на то, что выборка испытуемых разделилась на две категории (с плавными переходами между ними): одни справились с большинством заданий (согласились с большинством «ли-вопросов»), другие - не справились.
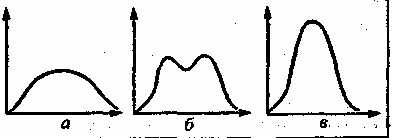
Рис. 3. Отрицательные (а, б) положительный (в) эксцессы распределения тестовых баллов
Такая конфигурация распределения свидетельствует о том, что в основе пунктов лежит какой-то один общий им всем признак, соответствующий определенному свойству испытуемых: если у испытуемых есть это свойство (способность, умение, знание), то они справляются с большинством пунктов, если этого свойства нет - то не справляются. В некоторых редких ситуациях пункты могут отрицательно коррелировать друг с другом. В этом случае на кривой возникает положительный эксцесс (рис. 3, в): вся масса эмпирических точек собирается вблизи среднего значения. Такое возможно в двух случаях: 1) когда ключ составлен неверно -объединены при подсчете отрицательно связанные признаки, которые обусловливают взаимоуничтожение баллов; 2) когда испытуемые применяют, разгадав направленность опросника, специальную тактику «медианного балла» - искусственно балансируют ответы «за» и «против» одного из полюсов измеряемого качества.
Итак, когда в качестве единственного эталона измерения психодиагностами рассматривается сам тест, то в качестве меры измеряемого свойства выступает положение балла на кривой распределения. Применяется процентильная шкала. В качестве универсальной меры, пригодной для разных (по своей качественной направленности и количеству пунктов) тестов, используется «процентильная мера». Процентилъ — процент испытуемых из выборки стандартизации, которые получили равный или более низкий балл, чем балл данного испытуемого. Таким образом, в качестве источника данной меры выступает нормативная выборка (выборка стандартизации), на которой построено нормативное распределение тестовых баллов. Процентильные шкалы лежат в основе всех традиционных шкал, применяемых в тестологии (Т-очки MMPI, баллы IQ, стены 16 PF и др.).
Подчеркнем, что с точки зрения теории измерений, процентильные шкалы относятся к порядковым шкалам: они дают информацию о том, у кого из испытуемых сильнее выражено измеряемое свойство, но не позволяют говорить о том, во сколько раз сильнее. Для того чтобы строить на базе таких шкал количественный прогноз, нужно повысить уровень измерения (популярное изложение представлений о теории измерений см. в книге: Клигер С. А. и др., 1978). Переход к шкалам интервалов производят либо на базе эмпирического распределения, либо на базе произвольной модели теоретического распределения. В абсолютном большинстве случаев в роли такой теоретической модели оказывается модель нормального распределения (хотя в принципе может быть использована любая модель).
В целом кроме статистических, процентильных шкал следует отличать нередко используемые в дифференциальной психометрике еще 2 вида шкал (и соответственно 2 вида тестовых норм). Это, во-первых, то, что можно условно назвать «абсолютными тестовыми нормами» — в роли шкалы для вынесения диагноза выступает сама шкала «сырых» очков, во-вторых, «критериальные» тестовые нормы. Применение таких норм можно считать оправданным в двух случаях: 1) когда сама тестовая «сырая» шкала имеет практический смысл (например, студент, изучающий иностранный язык, должен знать как можно больше слов этого языка, и сырой показатель лексического теста имеет практический смысл); 2) когда сырой балл по тесту в результате эмпирических исследований связывается с заданной вероятностью успешности какой-либо практической деятельности (вероятность успеха «критериальной» деятельности, каковой для упомянутого выше примера может быть синхронный перевод монолога в течение 30 минут).
Процентильная нормализация шкалы. Выше Показано, что нормальность распределения достигается искусственным подбором пунктов теста с заданными статистическими свойствами: Опишем еще ряд процедур, которые также широко используются для искусственной нормализации.
-
Нормализация пунктов. Ключ для данного пункта корректируется на базе нормальной модели. Если среди нормативной выборки с данным заданием справились только 16 % испытуемых, то данному пункту на интервальной шкале «трудности» (при условии априорного принятия нормальной модели с параметрами М = 0 и а = 1) соответствует значение +1 (см. график в книге: Анастазй А., 1982, с. 181). Если справились 75 % испытуемых, то балл пункта на сигма-шкале равен-0,67. В результате суммирования по пунктам баллов, скорректированных нормализацией, суммарные баллы лучше приближаются к нормальному распределению. -
Нормализация распределения суммарных баллов (или интервальная нормализация). В этом случае по таблице нормального распределения (нормального интеграла) производится переход от процентильной шкалы к сигма-шкале: используется функция, обратная интегральной, - от ординаты производится переход к абсциссе нормального распределения.
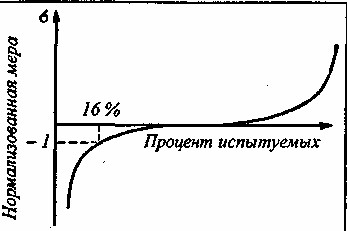
Рис. 4. Преобразование процентильной шкалы (по оси X) в нормализованную сигма-шкалу (по оси Y)
На рис. 4 дана условная графическая иллюстрация этого перехода (кривая, обратная традиционной S-образной интегральной кривой нормального распределения).
Приведем пример интервальной нормализации (табл. 3). Пусть строка X содержит сырые баллы (не нормализованные) по тесту, полученные простым подсчетом правильных ответов. В строке Р - частоты встречаемости сырых баллов в выборке из 62 испытуемых. В
i
строке F - кумулятивные частоты:Fi =Pji . В строке F* - кумулятив-
j1
ные баллы: Fi* Fi
PRi Fi* 100/n. В строке σ даются нормализованные баллы, полученные из соответствующих процентильных рангов по таблицам, а оценки часто называются в зарубежной литературе также z-оценками.
Таблица 3
| PR σ стен | 99 2,33 10 | 95 1,64 10 | 90 1,28 9 | 85 1,04 8 | 80 0,84 8 | 75 0,68 7 | 0 6 | |||
| PR σ стен | 50 0,0 5,5 | 45 - 0,13 5 | 40 - 0,25 | 35 - 0,39 4,5 | 30 - 0,52 4 | 25 - 0,68 4 | - 0,84 | |||
| | | | | | ||||||

