Файл: 1. Тип 20 26578 Из пункта a в пункт b одновременно выехали два автомобиля.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.11.2023
Просмотров: 152
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
км/ч.
Ответ: 70.
20. Тип 20 № 99607
Первые 190 км автомобиль ехал со скоростью 50 км/ч, следующие 180 км — со скоростью 90 км/ч, а затем 170 км — со скоростью 100 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Решение. Чтобы найти среднюю скорость на протяжении пути, нужно весь путь разделить на все время движения. Средняя скорость автомобиля равна
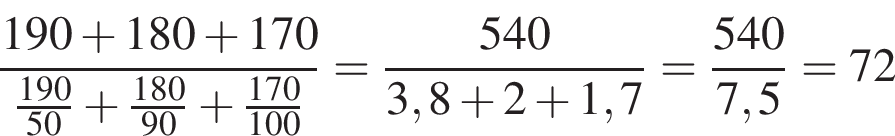км/ч.
Ответ: 72.
21. Тип 20 № 99608
Поезд, двигаясь равномерно со скоростью 80 км/ч, проезжает мимо придорожного столба за 36 секунд. Найдите длину поезда в метрах.
Решение. Скорость поезда равна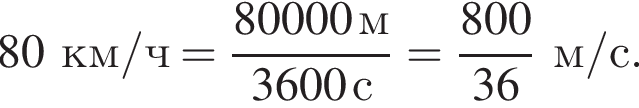
За 36 секунд поезд проходит мимо придорожного столба расстояние, равное своей длине:
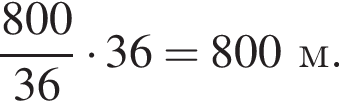
Ответ: 800.
22. Тип 20 № 99609
Поезд, двигаясь равномерно со скоростью 60 км/ч, проезжает мимо лесополосы, длина которой равна 400 метрам, за 1 минуту. Найдите длину поезда в метрах.
Решение. Скорость поезда равна 60 км в час, значит, за 1 минуту поезд проезжает 1 км. За это время поезд проезжает мимо лесополосы, то есть проходит расстояние, равное сумме длин лесополосы и самого поезда. Поэтому длина поезда равна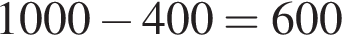
метров.
Ответ: 600.
23. Тип 20 № 99611
По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 90 км/ч и 30 км/ч. Длина товарного поезда равна 600 метрам. Найдите длину пассажирского поезда
, если время, за которое он прошел мимо товарного поезда, равно 1 минуте. Ответ дайте в метрах.
Решение. Скорость сближения поездов равна 60 км/ч или 1 км/мин. Следовательно, за 1 минуту пассажирский поезд сместится относительно товарного на 1 км. При этом он преодолеет расстояние, равное сумме длин поездов. Поэтому длина пассажирского поезда равна 1000 − 600 = 400 м.
Приведём другое решение.
Скорость сближения поездов равна
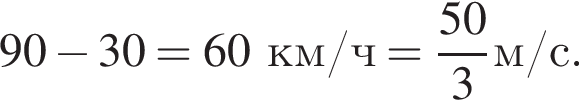
Пусть длина пассажирского поезда равна х метров. За 60 секунд один поезд проходит мимо другого, то есть преодолевает расстояние х + 600. Тогда:
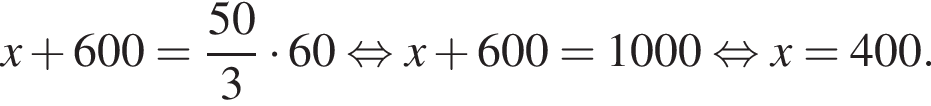
Поэтому длина пассажирского поезда 400 м.
Ответ: 400.
24. Тип 20 № 99612
По двум параллельным железнодорожным путям друг навстречу другу следуют скорый и пассажирский поезда, скорости которых равны соответственно 65 км/ч и 35 км/ч. Длина пассажирского поезда равна 700 метрам. Найдите длину скорого поезда, если время, за которое он прошел мимо пассажирского поезда, равно 36 секундам. Ответ дайте в метрах.
Решение. Относительная скорость поездов равна
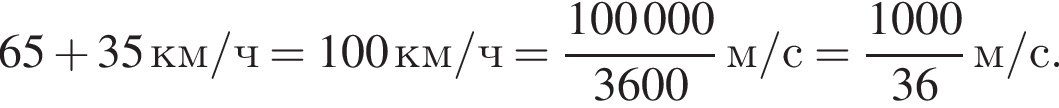
За 36 секунд один поезд проходит мимо другого, то есть вместе поезда преодолевают расстояние, равное сумме их длин:
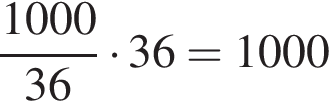м,
поэтому длина скорого поезда
Ответ: 300.
25. Тип 20 № 323849
Два человека отправляются из одного и того же места на прогулку до опушки леса, находящейся в 4,4 км от места отправления. Один идёт со скоростью 2,5 км/ч, а другой — со скоростью 3 км/ч. Дойдя до опушки, второй с той же скоростью возвращается обратно. На каком расстоянии от точки отправления произойдёт их встреча?
Решение. Пусть х км — искомое расстояние. Чтобы пройти это расстояние путнику, идущему со скоростью 2,5 км/ч, необходимо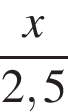
часа. Второй путник движется со скоростью 3 км/ч, поэтому чтобы пройти 4,4 км до опушки и вернуться на 
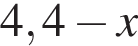км назад, ему необходимо 
+ 
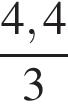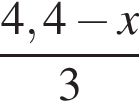часа. Времена движения путников равны, тогда:
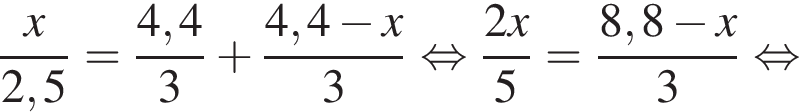
Тем самым, искомое расстояние равно 4 км.
Ответ: 4.
Приведем другое решение.
Пусть x ч — время, прошедшее от начала движения до момента встречи пешеходов. Тогда к моменту их встречи тот, кто шёл медленнее, прошёл 2,5x км, а тот, кто шёл быстрее, прошёл 4,4 км до опушки и ещё 3x км в обратном направлении. Пешеходы встретились на одном и том же расстоянии от опушки, поэтому расстояние, которое ещё осталось пройти до опушки более медленному из них, равно расстоянию, на которое более быстрый от неё уже удалился. Следовательно, 4,4 − 2,5х = 3х − 4,4, откуда х = 1,6 ч, а искомое расстояние равно 2,5 · 1,6 = 4 км.
Приведем другое решение.
Тот, кто идет быстрее, дойдет до опушки за 4,4 : 3 = 22/15 часа. За это время тот, кто идет медленнее, пройдет 2,5 · 22/15 = 11/3 км и окажется на расстоянии 4,4 − 11/3 = 11/15 км от опушки. Далее они пойдут на встречу друг другу со скоростью сближения 5,5 км/час и преодолеют разделяющее их расстояние за (11/15) : 5,5 = 2/15 часа. За это время медленно идущий пешеход пройдет еще 2,5 · 2/15 = 1/3 км и окажется на расстоянии 11/3 + 1/3 = 4 км от точки отправления.
26. Тип 20 № 323850
Дорога между пунктами А и В состоит из подъёма и спуска, а её длина равна 8 км. Турист прошёл путь из
А в В за 5 часов. Время его движения на спуске составило 1 час. С какой скоростью турист шёл на спуске, если скорость его движения на подъёме меньше скорости движения на спуске на 3 км/ч?
Решение. Пусть скорость, с которой турист спускался, равна х км/час, тогда его скорость на подъёме равна х − 3 км/ч, длина спуска равна х км, длина подъёма равна 4(х − 3) км. Поскольку весь путь равен 8 км, имеем: х + 4(х − 3) = 8, откуда х = 4 км/ч.
Ответ: 4.
27. Тип 20 № 323853
Иван и Алексей договорились встретиться в N-ске. Иван звонит Алексею и узнаёт, что тот находится в 275 км от N-ска и едет с постоянной скоростью 75 км/ч. Иван в момент разговора находится в 255 км от N-ска и ещё должен по дороге сделать 50-минутную остановку. С какой скоростью должен ехать Иван, чтобы прибыть в N-ск одновременно с Алексеем?
Решение. Время, необходимое Алексею, чтобы доехать до города, равно 275 : 75 = 11/3 часа или 3 часа 40 минут. Поскольку Иван должен сделать 50-минутную остановку, у него остаётся 2 часа 50 минут или 17/6 часа на движение. За это время он должен проехать 255 км, поэтому его скорость должна быть равной 255 : (17/6) = 90 км/час.
Ответ: 90.
28. Тип 20 № 503125
Дорога между пунктами А и В состоит из подъёма и спуска, а её длина равна 8 км. Пешеход прошёл путь из А в В за 2 часа 45 минут. Время его движения на спуске составило 1 час 15 минут. С какой скоростью пешеход шёл на спуске, если скорость его движения на подъёме меньше скорости движения на спуске на 2 км/ч? Ответ выразите в км/ч.
Решение. Заметим, что время подъема составило 1 час 30 минут или 1,5 часа, а время спуска 1,25 часа. Пусть x км/ч — скорость движения пешехода на спуске, тогда х − 2 км/ч — скорость движения пешехода на подъеме, 1,25х км — длина пути на спуске, 1,5(х − 2) км — длина пути на подъеме. Всего было пройдено 8 км, откуда имеем:
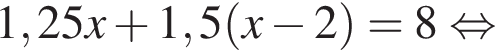
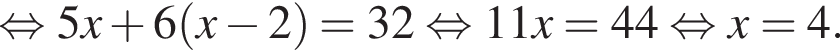
Тем самым, скорость пешехода на спуске была равна 4 км/ч.
Ответ: 4.
29. Тип 20 № 503316
Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 128 км. На следующий день он отправился обратно в А со скоростью на 8 км/ч больше прежней. По дороге он сделал остановку на 8 часов. В результате велосипедист затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из В в А. Ответ дайте в км/ч.
Решение. Пусть велосипедист ехал из А в В со скоростью x км/час, тогда обратно он ехал со скоростью
км/час. Разность времен на пути туда и обратно составляет 8 часов, откуда имеем:
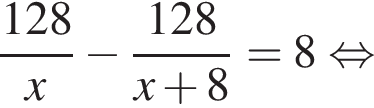
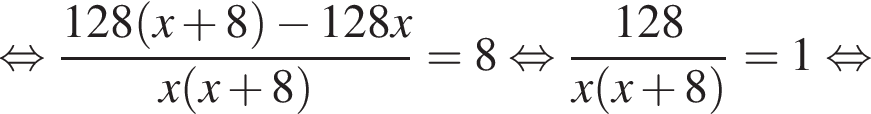
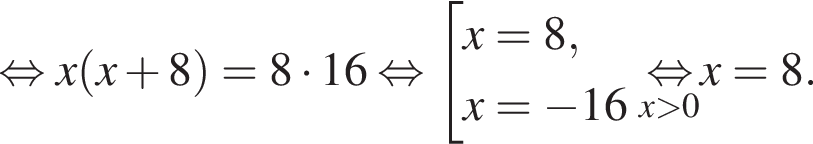
Искомая скорость велосипедиста на обратном пути на 8 км/час больше, поэтому она равна 16 км/час.
Ответ: 16.
30. Тип 20 № 523536
Два человека отправляются из одного дома на прогулку до опушки леса, находящейся в 5,5 км от дома. Один идёт со скоростью 2,5 км/ч, а другой — со скоростью 3 км/ч.
Ответ: 70.
20. Тип 20 № 99607
Первые 190 км автомобиль ехал со скоростью 50 км/ч, следующие 180 км — со скоростью 90 км/ч, а затем 170 км — со скоростью 100 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Решение. Чтобы найти среднюю скорость на протяжении пути, нужно весь путь разделить на все время движения. Средняя скорость автомобиля равна
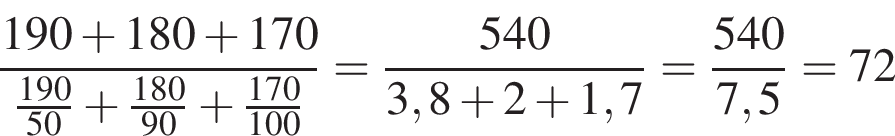км/ч.Ответ: 72.
21. Тип 20 № 99608
Поезд, двигаясь равномерно со скоростью 80 км/ч, проезжает мимо придорожного столба за 36 секунд. Найдите длину поезда в метрах.
Решение. Скорость поезда равна
За 36 секунд поезд проходит мимо придорожного столба расстояние, равное своей длине: Ответ: 800.
22. Тип 20 № 99609
Поезд, двигаясь равномерно со скоростью 60 км/ч, проезжает мимо лесополосы, длина которой равна 400 метрам, за 1 минуту. Найдите длину поезда в метрах.
Решение. Скорость поезда равна 60 км в час, значит, за 1 минуту поезд проезжает 1 км. За это время поезд проезжает мимо лесополосы, то есть проходит расстояние, равное сумме длин лесополосы и самого поезда. Поэтому длина поезда равна
метров.Ответ: 600.
23. Тип 20 № 99611
По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 90 км/ч и 30 км/ч. Длина товарного поезда равна 600 метрам. Найдите длину пассажирского поезда
, если время, за которое он прошел мимо товарного поезда, равно 1 минуте. Ответ дайте в метрах.
Решение. Скорость сближения поездов равна 60 км/ч или 1 км/мин. Следовательно, за 1 минуту пассажирский поезд сместится относительно товарного на 1 км. При этом он преодолеет расстояние, равное сумме длин поездов. Поэтому длина пассажирского поезда равна 1000 − 600 = 400 м.
Приведём другое решение.
Скорость сближения поездов равна
Пусть длина пассажирского поезда равна х метров. За 60 секунд один поезд проходит мимо другого, то есть преодолевает расстояние х + 600. Тогда:
Поэтому длина пассажирского поезда 400 м.
Ответ: 400.
24. Тип 20 № 99612
По двум параллельным железнодорожным путям друг навстречу другу следуют скорый и пассажирский поезда, скорости которых равны соответственно 65 км/ч и 35 км/ч. Длина пассажирского поезда равна 700 метрам. Найдите длину скорого поезда, если время, за которое он прошел мимо пассажирского поезда, равно 36 секундам. Ответ дайте в метрах.
Решение. Относительная скорость поездов равна
За 36 секунд один поезд проходит мимо другого, то есть вместе поезда преодолевают расстояние, равное сумме их длин:
м,поэтому длина скорого поезда
Ответ: 300.
25. Тип 20 № 323849
Два человека отправляются из одного и того же места на прогулку до опушки леса, находящейся в 4,4 км от места отправления. Один идёт со скоростью 2,5 км/ч, а другой — со скоростью 3 км/ч. Дойдя до опушки, второй с той же скоростью возвращается обратно. На каком расстоянии от точки отправления произойдёт их встреча?
Решение. Пусть х км — искомое расстояние. Чтобы пройти это расстояние путнику, идущему со скоростью 2,5 км/ч, необходимо
часа. Второй путник движется со скоростью 3 км/ч, поэтому чтобы пройти 4,4 км до опушки и вернуться на км назад, ему необходимо + часа. Времена движения путников равны, тогда: Тем самым, искомое расстояние равно 4 км.
Ответ: 4.
Приведем другое решение.
Пусть x ч — время, прошедшее от начала движения до момента встречи пешеходов. Тогда к моменту их встречи тот, кто шёл медленнее, прошёл 2,5x км, а тот, кто шёл быстрее, прошёл 4,4 км до опушки и ещё 3x км в обратном направлении. Пешеходы встретились на одном и том же расстоянии от опушки, поэтому расстояние, которое ещё осталось пройти до опушки более медленному из них, равно расстоянию, на которое более быстрый от неё уже удалился. Следовательно, 4,4 − 2,5х = 3х − 4,4, откуда х = 1,6 ч, а искомое расстояние равно 2,5 · 1,6 = 4 км.
Приведем другое решение.
Тот, кто идет быстрее, дойдет до опушки за 4,4 : 3 = 22/15 часа. За это время тот, кто идет медленнее, пройдет 2,5 · 22/15 = 11/3 км и окажется на расстоянии 4,4 − 11/3 = 11/15 км от опушки. Далее они пойдут на встречу друг другу со скоростью сближения 5,5 км/час и преодолеют разделяющее их расстояние за (11/15) : 5,5 = 2/15 часа. За это время медленно идущий пешеход пройдет еще 2,5 · 2/15 = 1/3 км и окажется на расстоянии 11/3 + 1/3 = 4 км от точки отправления.
26. Тип 20 № 323850
Дорога между пунктами А и В состоит из подъёма и спуска, а её длина равна 8 км. Турист прошёл путь из
А в В за 5 часов. Время его движения на спуске составило 1 час. С какой скоростью турист шёл на спуске, если скорость его движения на подъёме меньше скорости движения на спуске на 3 км/ч?
Решение. Пусть скорость, с которой турист спускался, равна х км/час, тогда его скорость на подъёме равна х − 3 км/ч, длина спуска равна х км, длина подъёма равна 4(х − 3) км. Поскольку весь путь равен 8 км, имеем: х + 4(х − 3) = 8, откуда х = 4 км/ч.
Ответ: 4.
27. Тип 20 № 323853
Иван и Алексей договорились встретиться в N-ске. Иван звонит Алексею и узнаёт, что тот находится в 275 км от N-ска и едет с постоянной скоростью 75 км/ч. Иван в момент разговора находится в 255 км от N-ска и ещё должен по дороге сделать 50-минутную остановку. С какой скоростью должен ехать Иван, чтобы прибыть в N-ск одновременно с Алексеем?
Решение. Время, необходимое Алексею, чтобы доехать до города, равно 275 : 75 = 11/3 часа или 3 часа 40 минут. Поскольку Иван должен сделать 50-минутную остановку, у него остаётся 2 часа 50 минут или 17/6 часа на движение. За это время он должен проехать 255 км, поэтому его скорость должна быть равной 255 : (17/6) = 90 км/час.
Ответ: 90.
28. Тип 20 № 503125
Дорога между пунктами А и В состоит из подъёма и спуска, а её длина равна 8 км. Пешеход прошёл путь из А в В за 2 часа 45 минут. Время его движения на спуске составило 1 час 15 минут. С какой скоростью пешеход шёл на спуске, если скорость его движения на подъёме меньше скорости движения на спуске на 2 км/ч? Ответ выразите в км/ч.
Решение. Заметим, что время подъема составило 1 час 30 минут или 1,5 часа, а время спуска 1,25 часа. Пусть x км/ч — скорость движения пешехода на спуске, тогда х − 2 км/ч — скорость движения пешехода на подъеме, 1,25х км — длина пути на спуске, 1,5(х − 2) км — длина пути на подъеме. Всего было пройдено 8 км, откуда имеем:
Тем самым, скорость пешехода на спуске была равна 4 км/ч.
Ответ: 4.
29. Тип 20 № 503316
Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 128 км. На следующий день он отправился обратно в А со скоростью на 8 км/ч больше прежней. По дороге он сделал остановку на 8 часов. В результате велосипедист затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из В в А. Ответ дайте в км/ч.
Решение. Пусть велосипедист ехал из А в В со скоростью x км/час, тогда обратно он ехал со скоростью
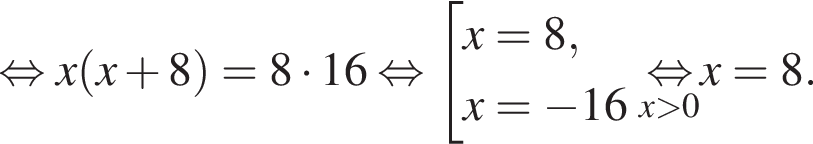
км/час. Разность времен на пути туда и обратно составляет 8 часов, откуда имеем: Искомая скорость велосипедиста на обратном пути на 8 км/час больше, поэтому она равна 16 км/час.
Ответ: 16.
30. Тип 20 № 523536
Два человека отправляются из одного дома на прогулку до опушки леса, находящейся в 5,5 км от дома. Один идёт со скоростью 2,5 км/ч, а другой — со скоростью 3 км/ч.