ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.11.2023
Просмотров: 609
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Базисная схема предусматривает сравнение анализируемого показателя (уровня ряда динамики) с аналогичным, относящегося к одному и тому же периоду (году). Прицепном методе анализа каждый последующий уровень ряда сравнивается (сопоставляется) с предыдущим.
| Год | Усл. обоз | Объем произ-ва млн.руб. | Абсолютный прирост | Темп роста | Темп прироста | Знач. 1% прироста | ||||||
| баз. | цепн. | баз. | цепн. | баз. | цепн. | П=Аi /Ti П=0.01Yi-1 | ||||||
| Yi-Y0 | Yi-Yi-1 | Yi/Y0 | Yi/Yi-1 | T=Tр-100 | ||||||||
| 2000 | Y0 | 17,6 | - | - | - | - | - | - | - | |||
| 2001 | Y1 | 18,0 | 0,4 | 0,4 | 102 | 102 | 2 | 2 | 0,17 | |||
| 2002 | Y2 | 18,9 | 1,3 | 0,9 | 107 | 105 | 7 | 5 | 0,18 | |||
| 2003 | Y3 | 22,7 | 5,1 | 3,8 | 129 | 120 | 29 | 20 | 0,19 | |||
| 2004 | Y4 | 25,0 | 7,4 | 2,3 | 142 | 110 | 42 | 10 | 0,23 | |||
| 2005 | Y5 | 30,0 | 12,4 | 5,0 | 170 | 120 | 70 | 20 | 0,25 | |||
| 2006 | Y6 | 37,0 | 19,4 | 7,0 | 210 | 123 | 110 | 23 | 0,30 | |||
| У | | 169,2 | | 19,4 | | | | | | |||
Определение среднегодовых показателей с применением формул расчета для средней (средняя арифметическая простая, средняя геометрическая простая).
1) Опр. среднегодовой абсолютный прирост:
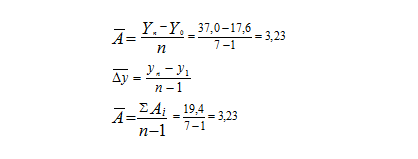
2) Опр. среднегодовой коэффициент (темп) роста:
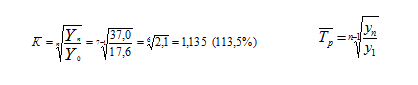
Либо по средней геометрической простой:
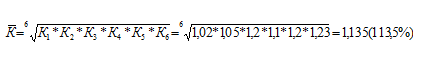
3) Опр. среднегодовой темп прироста:
-
Средний уровень ряда: определение и методика расчета.
Средний уровень ряда определяет обобщенную величину абсолютных уровней. Он определяется по средней, исчисленной из значений, меняющихся во времени. Методы расчета среднего уровня интервального и моментного рядов динамики разные.
Средний уровень из абсолютных уровней для интервальных рядов динамики рассчитывается по формуле средней арифметической:
1. При равных интервалах используют среднюю арифметическую простую:
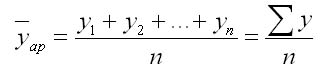
где у — абсолютные уровни ряда;
n — число уровней ряда.
2. При неравных интервалах используют среднюю арифметическую взвешенную:
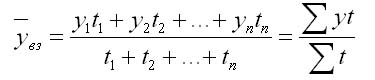
где у1,...,уn — уровни ряда динамики;
t1,... tn — веса, длительность интервалов времени.
Средний уровень моментного ряда динамики рассчитывается по формуле:
1. С равностоящими уровнями рассчитывается по формуле средней хронологической моментного ряда:
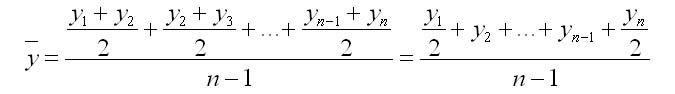
где у1,...,уn — уровни периода, за который делается расчет;
n — число уровней;
n-1 — длительность периода времени.
2. С неравностоящими уровнями рассчитывается по формуле средней хронологической взвешенной:
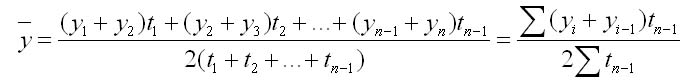
где у1,...,уn — уровни рядов динамики;
t — интервал времени между смежными уровнями
^
Средний абсолютный прирост в задачах статистики
Средний абсолютный прирост определяется как среднее из абсолютных приростов за равные промежутки времени одного периода. Он рассчитывается по формулам:
1. По цепным данным об абсолютных приростах за ряд лет рассчитывают средний абсолютный прирост как среднюю арифметическую простую:
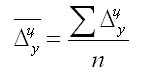
где n — число степенных абсолютных приростов в исследуемом периоде.
2. Средний абсолютный прирост рассчитывают через базисный абсолютный прирост в случае равных интервалов
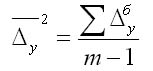
где m — число уровней ряда динамики в исследуемом периоде, включая базисный.
^
Средний темп роста
Средний темп роста есть свободная обобщающая характеристика интенсивности изменения уровней ряда динамики и показывает, во сколько раз в среднем за единицу времени изменяется уровень ряда динамики.
В качестве основы и критерия правильности вычисления среднего темпа роста (снижения) применяется обобщающий показатель, который рассчитывается как произведение цепных темпов роста, равное темпу роста за весь рассматриваемый период. Если значение признака образуется как произведение отдельных вариантов, то используют среднюю геометрическую.
Так как средний темп роста представляет собой средний коэффициент роста, выражен в процентах, то для равностоящих рядов динамики расчеты по средней геометрической сводятся к вычислению средних коэффициентов роста из цепных по «цепному способу»:
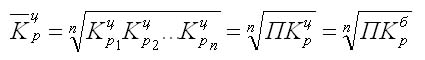
где n — число цепных коэффициентов роста;
Кц — цепные коэффициенты роста;
Кб — базисный коэффициент роста за весь период.
Определение среднего коэффициента роста может быть упрощено, если будут ясны уровни динамического ряда. Так как произведение цепных коэффициентов роста равно базисному, то в подкоренное выражение подставляют базисный коэффициент роста.
Формула для определения среднего коэффициента роста
для равностоящих рядов динамики по «базисному способу» будет такая:
^
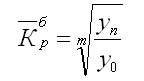
Средний темп прироста
Средние темпы прироста рассчитываются на основе средних темпов роста (Тр) вычитанием из последних 100%:
Для того, чтобы определить средний коэффициент прироста (Кпр), нужно из значений коэффициентов роста (Кр) вычесть единицу.
-
Проверка ряда на наличие тренда: метод средних; фазочастотный критерий знаков первой разницы; метод Стюарта-Кокса.
Прежде чем приступать к решению задачи аналитического сглаживания динамических рядов (аналитическое описание общей тенденции развития регрессионными моделями), необходимо проверить существенность трендовой составляющей динамического ряда.
Проверка проводится с помощью двух критериев:
1) Фазочастотный критерий Валлиса-Мура.
Этот критерий позволяет отличить отклонения последовательности уровней ряда от чисто случайной последовательности. Если тренд отсутствует, то знаки разностей значений уровней
образуют случайную последовательность.
С помощью критерия Валлиса-Мура проверяется гипотеза:
последовательность знаков разностей имеет случайный характер.
Альтернативной к ней является гипотеза:
последовательность знаков разностей значимо отличается от случайной.
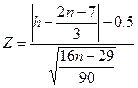где h – число плюсовых и минусовых разностейn – число уровней ряда
2) Знаковый критерий Кокса-Стюарта
Для использования критерия n уровней ряда делится на 3 равные части
Критерий строится на оценке знаков разностей начальной (первой) и конечной (третьей) частей динамического ряда. Расчет строится на сопоставлении одноименных уровней ряда и фиксировании знаков разностей:
При этом отрицательной разности присваивается «+», а положительной «-»
Проверяется гипотеза об отсутствии тренда через сравнение расчетного и табличного значений
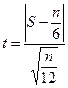где S – наибольшее значение среди «+» и «-»В рамках курсового проекта рассматривается фазочастотный критерий Валлиса-Мура.
| Год | Абсолютное изменение | Знак изменения |
| 1983 год | -2,446 | - |
| 1984 год | 0,145 | + |
| 1985 год | 5,466 | + |
| 1986 год | 32,384 | + |
| 1987 год | 37,569 | + |
| 1988 год | 22,026 | + |
| 1989 год | 19,235 | + |
| 1990 год | 76,451 | + |
| 1991 год | 43,755 | + |
| 1992 год | 12,532 | + |
| 1993 год | -56,413 | - |
| 1994 год | 39,324 | + |
| 1995 год | 78,92 | + |
| 1996 год | -5,488 | - |
| 1997 год | -17,041 | - |