ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.11.2023
Просмотров: 604
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
- сумма наблюдений, накопленная до начала медианного интервала;
- число наблюдений в медианном интервале.
Средний уровень ряда характеризует обобщенную величину абсолютных уровней. Он рассчитывается по средней хронологической, т.е. по средней исчисленной из значений, изменяющихся во времени.
-
Показатели вариации: назначение и методика расчета.
В практическом анализе оценка рассеяния значений признака может оказаться не менее важной, чем определение средней.
Самая грубая оценка рассеяния, легко определяемая по данным вариационного ряда, может быть дана с помощью размаха вариации –характеризует границы вариации изучаемого признака.
где xmax и xmin- наибольшее и наименьшее значения варьирующего признака.
Показывает, на сколько велико различие между единицами совокупности, имеющими самое маленькое и самое большое значение признака. Показатель основан на крайних значениях варьирующего признака и не отражает отклонений всех вариант в ряду.
Однако этот показатель не дает представления о характере вариационного ряда, расположении вариантов вокруг средней и может сильно меняться, если добавить или исключить крайние варианты (когда эти значения аномальны для данной совокупности). В этих случаях размах вариации дает искаженную амплитуду колебания против нормальных ее размеров. Поэтому следует очистить совокупность от аномальных наблюдений, прежде чем определять размах вариации.
Для оценки колеблемости значений признака относительно средней используются характеристики рассеяния. Они различаются выбранной формой средней и способами оценки отклонений от нее отдельных вариантов. К таким показателям относятся:
- среднее линейное отклонение;
- дисперсия;
- среднее квадратическое отклонение;
- коэффициент вариации.
Среднее линейное отклонение есть средняя арифметическая из абсолютных значений отклонений отдельных вариантов от их средней величины:
| | для несгруппированных данных |
| | для сгруппированных данных |
где xi - значение признака в дискретном ряду или середина интервала в интервальном распределении;
fi - частота признака.
Среднее линейное отклонение выражено в тех же единицах измерения, что и варианты или их средняя. Оно дает абсолютную меру вариации. Показывает, на какую величину отклоняется признак в изучаемой совокупности от средней величины признака.
Чтобы избежать равенства нулю суммы отклонений от средней, используют либо абсолютные значения отклонений, либо их четные степени, например квадраты. В последнем случае мера вариации называется дисперсией и обозначается D или s2:
Дисперсия представляет собой средний квадрат отклонений индивидуальных значений признака от их средних величин. В зависимости от исходных данных вычисляется по формулам:
| | для несгруппированных данных |
| | для сгруппированных данных |
Расчет дисперсии может быть упрощен.
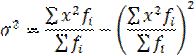
Вследствие суммирования квадратов отклонений дисперсия дает искаженное представление об отклонениях, измеряя их в квадратных единицах. Поэтому на основе дисперсии вводятся еще две характеристики: среднее квадратическое отклонение и коэффициент вариации.
Среднее квадратическое отклонение измеряется в тех же единицах, что и варьирующий признак, и исчисляется путем извлечения квадратного корня из дисперсии:
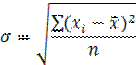 | для несгруппированных данных |
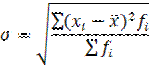 | для сгруппированных данных |
Среднее квадратическое отклонение, как и среднее линейное отклонение, показывает, на сколько в среднем отклоняются конкретные варианты признака от его среднего значения. Величина о часто используется в качестве единицы измерения отклонений от средней арифметической. Отклонение, выраженное в s, называется нормированным или стандартизированным.
Коэффициент вариации – характеризует меру вариации значений признака вокруг средней величины. Дает относительную оценку вариации и получается путем сопоставления среднего линейного или среднего квадратического отклонения со средним уровнем явления, а результат выражается в процентах:
Чем коэффициент меньше, тем однороднее совокупность и наоборот, чем больше тем неоднороднее.
Так как коэффициенты вариации дают относительную характеристику однородности явлений и процессов, они позволяют сравнивать степень вариации разных признаков.
| Линейный коэффициент вариации | |
| Коэффициент осциляции | |
-
Статистические таблицы и правила их построения.
Статистические таблицы позволяют охватить материал статистической сводки в целом. Макет таблицы – это строки по горизонтали и столбцы (графы) по вертикали, образованные пересекающимися линиями, т.е. скелет таблицы, не заполненный цифрами.
Статистическая таблица имеет подлежащее и сказуемое. Подлежащее показывает, о каком явлении идёт речь и представляет собой группы и подгруппы. Сказуемым таблицы называются показатели, характеризующие подлежащее (изучаемый объект), в основном, это численные значения. Подлежащее обычно располагается в левой части таблицы, а сказуемое – в правой части.
Статистическая таблица должна иметь общий, боковые и верхние заголовки. Общий заголовок располагается над таблицей, боковые раскрывают содержание подлежащего (строк), а верхние – содержание сказуемого (граф).
В зависимости от построения подлежащего таблицы бывают простые, групповые и комбинационные в соответствии с материалом сводки и группировки.
В подлежащем простых таблиц указывается перечневой, территориальный или хронологический материал.
Данная таблица содержит в подлежащем перечень единиц изучаемой совокупности.
В подлежащем групповых таблиц указываются конкретные группы по существенному признаку или группы, позволяющие выявить связи между показателями.
Данная таблица должна показать взаимосвязь между объёмом товарооборота и эффективностью использования торговой площади.
Для многостороннего анализа используются комбинационные таблицы, в которых каждая группа подлежащего по одному признаку делится на подгруппы по второму признаку и т.д.
Разработка сказуемого также бывает простой и сложной. При простой показатели сказуемого располагаются последовательно, один за другим. При сложной показатели сказуемого распределяются на группы по одному или нескольким признакам в определённом сочетании.
Правила составления таблиц.
1. Таблица должна быть небольшой по размеру, легко обозримой.
2. Общий заголовок должен кратко выражать основное содержание таблицы, т.е. указывать время, территорию, единицу измерения (если она едина). Заголовки строк и граф также формулируются кратко и ясно. Слова в таблице пишутся полностью.
3. При неполном объёме единиц совокупности или отсутствии исходных данных слагаемые (суммы) сначала показывают в строке «общие итоги», и, после строки «в том числе», перечисляют их составные части.
4. Для удобства анализа столбцы, содержащие подлежащее и сказуемое, нумеруются: с подлежащим и единицами измерения – буквами, со сказуемым – цифрами по порядку.
5. Применяются условные обозначения: при отсутствии явления прочерк (« – »); если нет информации – многоточие («...») или «нет сведений»; если значение признака не имеет смысла, ставится «Х» (например, состояние в браке в возрасте 0-10 лет); если значение признака меньше принятого, ставится «0,0».
6. Все числа в таблице должны быть с одинаковой степенью точности (один знак после запятой, два, три и т.д.). Также должны соблюдаться правила округления чисел. В случаях, когда одна величина превосходит другую многократно, показатели лучше выражать не в процентах, а в разах (пишется словами: в 2,5 раза и т.п.).
7. Когда в таблице, наряду с фактическими данными, приводятся сведения расчётного характера, делается пояснение в самой таблице, либо в заголовке таблицы, можно оформить примечанием.
-
Статистические графики: основные элементы и виды.
Статистический график -условное изображение, посредством которого статистической совокупности, характеризуемые определенными показателями, отображаются в виде различных геометрических образов-линий, точек, плоскостных или объемных фигур, а также разнообразных символов.
Элементы графика: