Задача 1.1. Расчет стержня

Условие задачи: Стержень, жестко закрепленный одним концом, состоящий из 3-х участков длиной 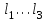и площадью 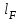, находится под действием собственного веса и силы , приложенной на координате . Материал стержня – ст. 3.

Требуется: Построить эпюры продольных сил 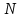, нормальных напряжений 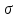и перемещений .

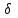Дано: 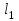=1,1 м, 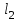=1,0 м, 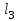=0,6 м, 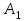=40 см² , 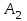=20 см², 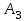=30 см², 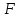=70 кН, 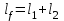, опора внизу.

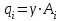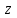Указания: Собственный вес стержня можно представить в виде распределенной нагрузки . Ось , направление силы 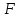и нумерацию участков вести от опоры.

Решение: Вычертим схему стержня в соответствии с исходными данными из табл. 1.1 и указаниями к задаче (см. рис. 1.1). Расчет начнем со свободного конца стержня, т.е. с III-го участка. На силовом участке рассекаем стержень и, отбрасывая часть стержня, содержащую опору, составляем уравнения .

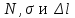Участок III:

---

, , ,

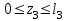
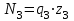
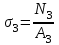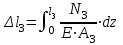где .

Получаем

при , ;

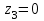
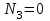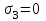при

= ,



= ;



= .

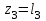
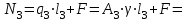
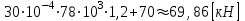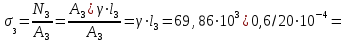
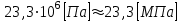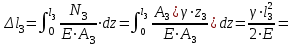
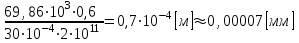Аналогично производим расчет на участках II и I. Далее определяем перемещения сечений стержня:

, , ,.

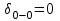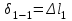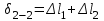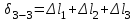
Результаты расчетов сведены в таблицу, а эпюры представлены на рис. 1.1.

Участок	Границы участка	Продольная сила N, кН	Нормальное напряжение , Мпа	Перемещение , мм
III	начало	0	0	0,2693
	конец	69,86	34,93	0,2694
II	начало	69,86	34,93	0,2694
	конец	69,70	34,89	0,0954
I	начало	69,70	17,43	0,0954
	конец	69,36	17,34	0

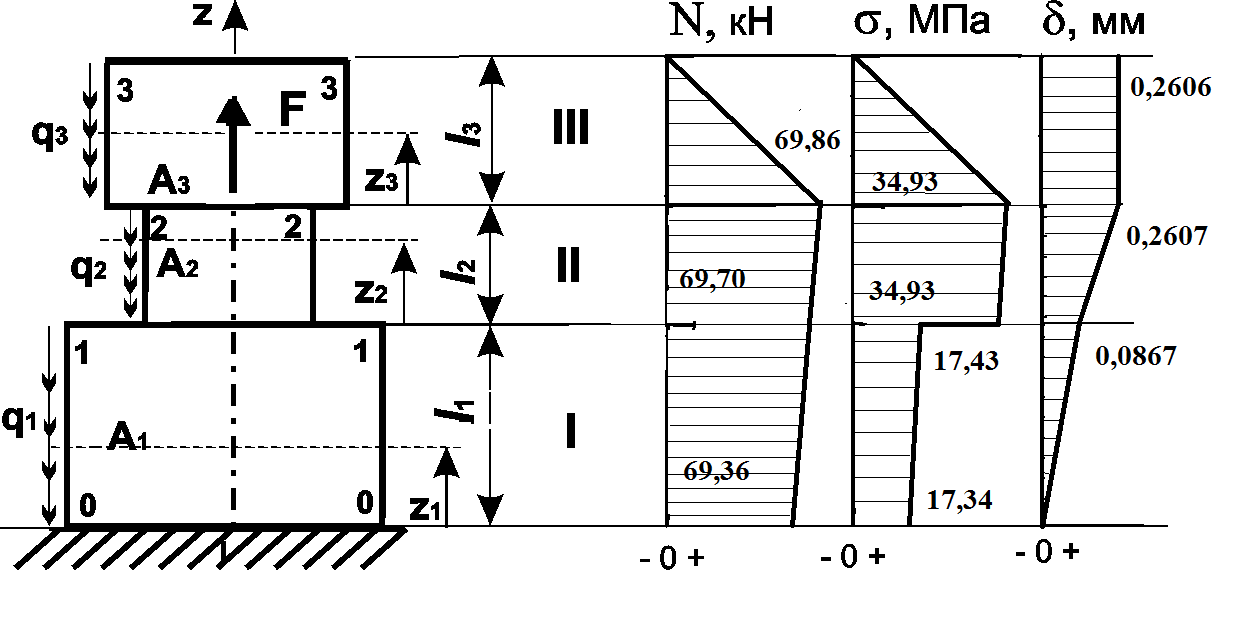
Рис. 1.1.

Задача 1.2.

---

Расчет статически-неопределимого стержня
Условие задачи: Стержень, жестко закрепленный одним концом (A), состоящий из 2-х участков длиной 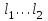и площадью 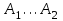, находится под действием приложенной на границе участков силы и разности температур . На расстоянии от свободного конца стержня расположена вторая опора (B). Материал участков стержня различен.

Требуется: Построить эпюры продольных сил , нормальных напряжений и перемещений .

Дано: =0,7 м, =1,3 м, =40 см² , =30 см², =40 кН, опора вверху, сталь-латунь, 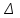=0,35 мм,. =32°С

Указания: Предварительно определите, будут ли деформации стержня от действия силы и разности температур превышать значение зазора , т.е. будет ли стержень статически неопределим. Собственным весом стержня пренебречь. Ось

---

, направление силы и нумерацию участков вести от опоры.

Решение: Вычертим схему стержня в соответствии с исходными данными из табл. 1.1 и 1.2 и указаниями к задаче (см. рис. 1.2).

_{Определим деформацию стержня от действия силы}

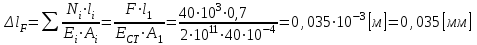и разности температур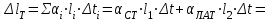



=

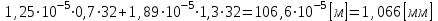
Т.о. деформация стержня от действия силы и разности температур составляет 1,101 мм, что превышает значение зазора 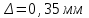, следовательно, стержень упирается во вторую опору и в результате возникает реакция .

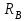Т.к. стержень становится статически неопределимым, уравнений статики недостаточно для нахождения его опорных реакций. Составим дополнительное уравнение, а именно уравнение деформации стержня.

,

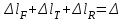где

=

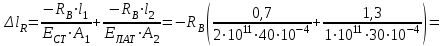
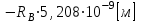
Решая дополнительное уравнение, получим .

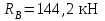Теперь система статически определена, начнем расчет аналогично предыдущей задаче.

Участок II:

,

,



=

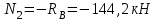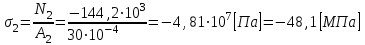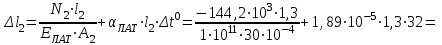
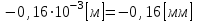
Аналогично производим расчет на I участке.

Далее определяем перемещения сечений стержня:

, ,

---

.


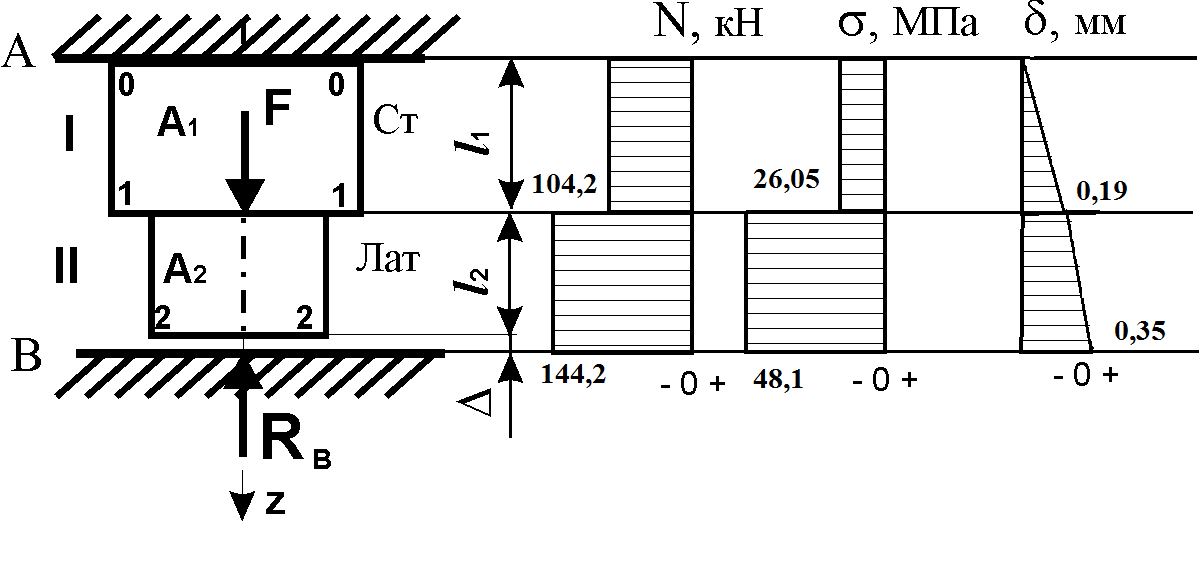
Рис. 1.2

Результаты расчетов сведены в таблицу, а эпюры представлены на рис. 1.2. Обратите внимание, что .

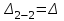Участок	Продольная сила N, кН	Нормальное напряжение , МПа	Перемещение , мм
I	-104,2	-26,05	0,19
II	-144,2	-48,1	0,35

Задача 1.3. Расчет статически-неопределимой

шарнирно-стержневой системы
Условие задачи: Горизонтально расположенный абсолютно жесткий брус, с приложенной к нему силой , опирается на шарнирно-неподвижную опору О и стержни AB и CD, концы которых шарнирно закреплены.

Требуется: Определить из условия прочности стержней AB и CD допустимую силу .

Дано: а=0,9 м, b=0,5 м, c=0,6 м, d =1,5 м, f=1,3 м, 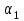= 45°, =10 см² , =20 см² , 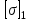= 100 МПа, 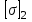= 210 МПа.

Указання: Модули упругости стержней считайте одинаковыми, т.е. 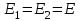. При составлении расчетной схемы координаты шарниров откладывайте в соответствии с направлениями осей 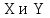: положительные значения – в положительном направлении осей, т.е. вверх и вправо, а отрицательные – наоборот, т.е. вниз и влево. Углы 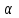откладывайте к горизонтали.

Решение: Составим уравнение статики для стержневой системы

---

Смотрите также файлы

• 4. Вопрос.docx

• Республики Узбекистан Филиал государственного бюджетного образовательного учреждения высшего.pdf

• Решение 1 2000(110)220000156000 2 1 год 200011%220 2 год 200022%400 2 задание.docx

• Согласие на обработку персональных данных 16.docx

• И. О. Фамилия Малоэтажный блокированный дом.docx