Добавлен: 06.11.2023
Просмотров: 109
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
- перемещения конца балки по осям X и Y, которые определим методом начальных параметров.
Начало координат выбираем в заделке (т. О), где начальные параметры - прогиб и угол поворота сечения равны нулю.
Предварительно определим опорные реакции и жесткость сечения:
,
,
,
.
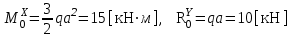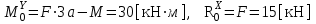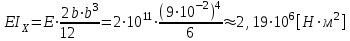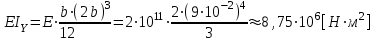Составим уравнения прогибов по методу начальных параметров:
.
,
.
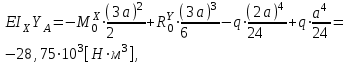
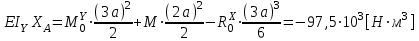Окончательно получаем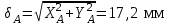
.
Задача 5.2. Внецентренное растяжение (сжатие)
Условие задачи: На короткий стержень действует сжимающая сила F, приложенная в полюс (точку p).
Требуется: Определим допускаемую нагрузку F из условия прочности.
Исходные данные к задаче 5.2
Таблица 5.2
Указания:. Форма сечения представлена на рис.4.2.1. Полюс р назначьте в точке сечения с максимальными координатами X и Y.
Решение: Определим положение центра тяжести сечения (относительно оси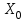
) и осевые моменты инерции сечения (см. рис. 5.2.1). Пример такого расчета представлен в задаче 4.2.
В нашем примере (расчет не приводим) получено:
, 
, 
, 
.
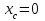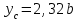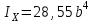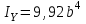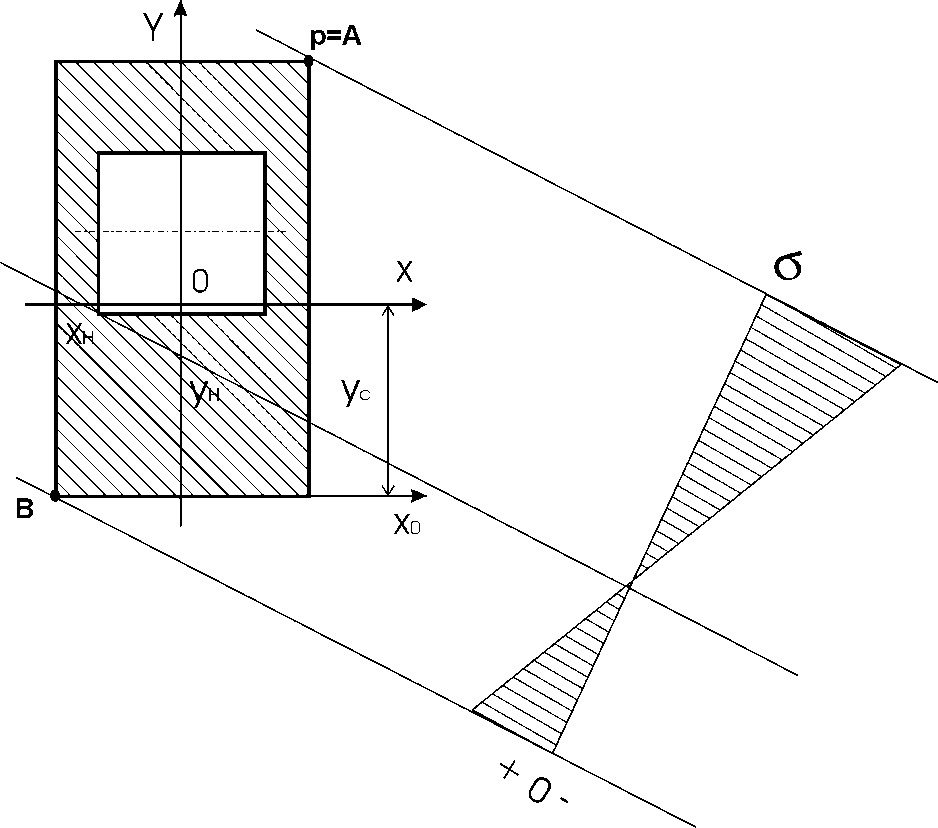
Рис. 5.2.1.
Определим положение нейтральной линии по координатам ее пересечения с осями X и Y :
,
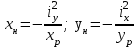где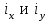
- радиусы инерции сечения, 
.
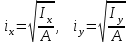Произведя расчет, получаем
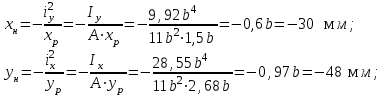
и, отложив эти координаты на оси X и Y, проводим через них нейтральную линию.
Выполним подбор допускаемой нагрузки из условия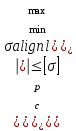
.
Максимальные и минимальные напряжения в наиболее удаленных от нейтральной линии точках сечения (это точка А, совпадающая с полюсом р и точка В) определим по формулам:
; 
.
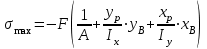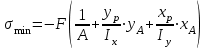Произведем расчет:
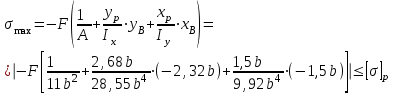
откуда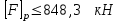
;
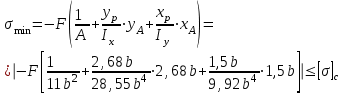
откуда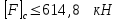
.
Окончательно принимаем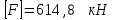
.
Задача 5.3. Изгиб с кручением
Условие задачи: На валу круглого сечения, вращающемся с угловой частотой
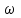, расположены два шкива ременной передачи диаметрами 
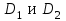, через которые передается мощность NЭД. Вал закреплен в подшипниковых опорах A и B. Ветви шкива 1 расположены под углом 
, а шкива 2 - под углом 
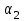к горизонтали.
Требуется: Подобрать диаметра вала по III теории прочности при заданном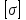
.
Указания:. Опору А расположите в начале координат, опору В на координате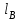
, шкивы 1 и 2 соответственно на координатах 
.
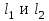Решение: Определим момент
, действующий на участке вала между шкивами 1 и 2
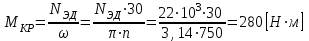
и построим эпюру крутящих моментов.
Определим усилия
в ремённой передаче:
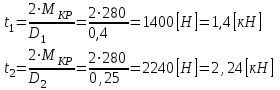
Опорные реакции, необходимые для построения эпюр, определим из уравнений статики:
;
.
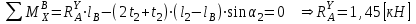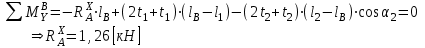и строим эпюры изгибающих моментов
.
Затем строим эпюру суммарного изгибающего момента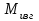
, являющегося векторной суммой моментов , т.е.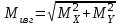 
.
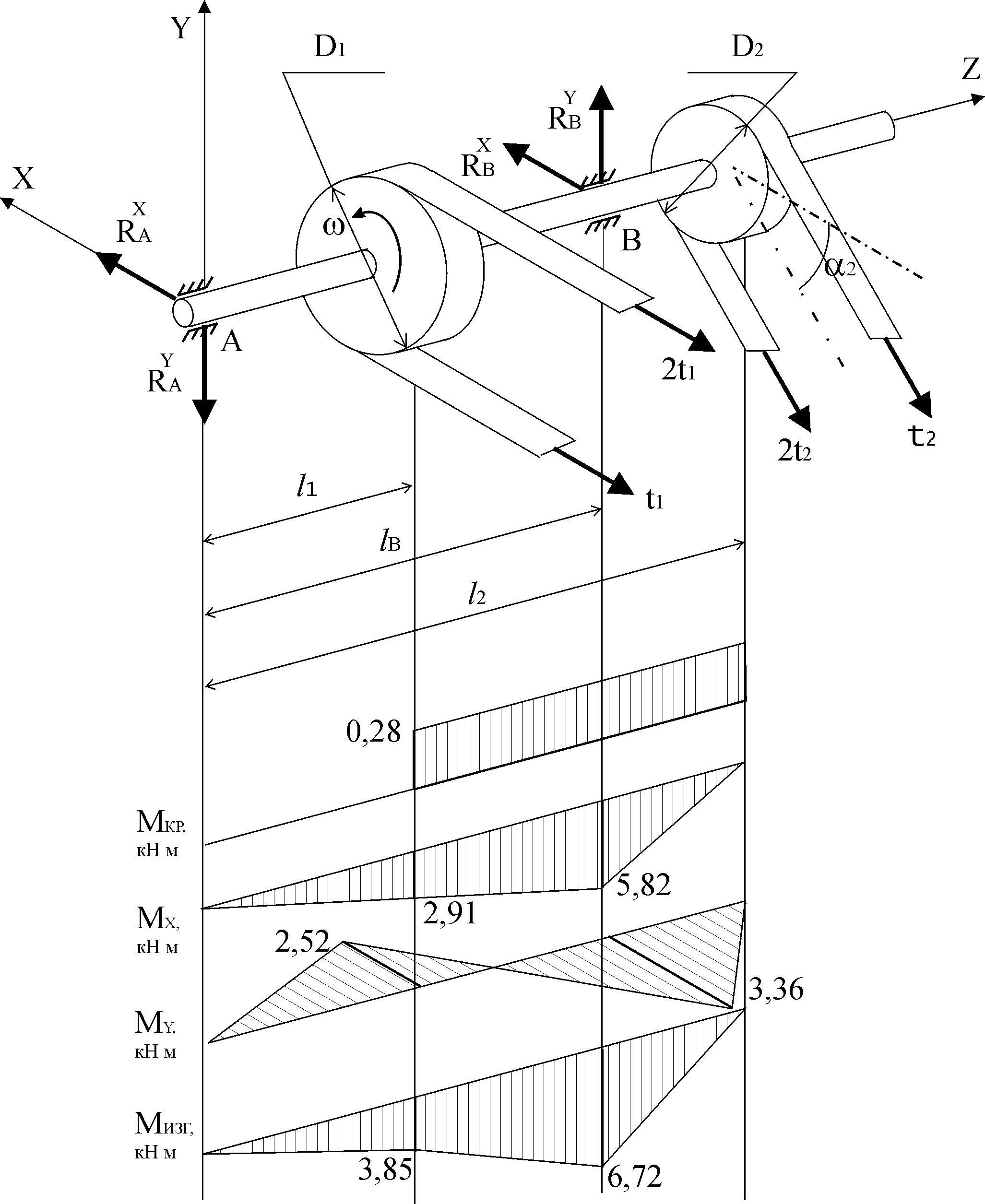
Рис. 5.3.1.
По эпюре
определяем опасное сечение вала по максимальному изгибающему моменту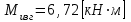 
.
Произведем подбор сечения вала по условию прочности:
,
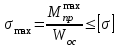где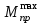
- приведенный момент, по III теории прочности
;
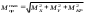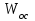- осевой момент сопротивления сечения,
для круглого сечения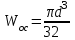
.
Вычислим диаметр:
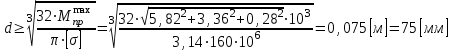
Принимаем d=80 мм.
Тема 6. Напряженное состояние
Задача 6.1. Плоское напряженное состояние
Условие задачи: На грани кубика действует нормальное напряжение по двум взаимно перпендикулярным направлениям, а также касательные напряжения.
Требуется: Найти главные напряжения в направлении главных площадок, относительные деформации, относительное изменение объема и удельную потенциальную энергию деформации.
Исходные данные к задаче 6.1
Таблица 6.1
Начало координат выбираем в заделке (т. О), где начальные параметры - прогиб и угол поворота сечения равны нулю.
Предварительно определим опорные реакции и жесткость сечения:
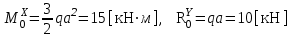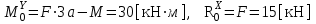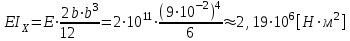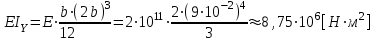, , , .Составим уравнения прогибов по методу начальных параметров:
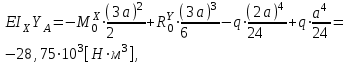
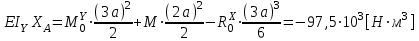. , .Окончательно получаем
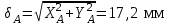.Задача 5.2. Внецентренное растяжение (сжатие)
Условие задачи: На короткий стержень действует сжимающая сила F, приложенная в полюс (точку p).
Требуется: Определим допускаемую нагрузку F из условия прочности.
Исходные данные к задаче 5.2
Таблица 5.2
| Данные | Сечение (рис.4.2.1) | b, мм |  |  |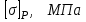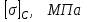
| 0 | 2 | 80 | 90 | 150 |
| 1 | 1 | 50 | 120 | 180 |
| 2 | 4 | 60 | 80 | 170 |
| 3 | 2 | 70 | 110 | 140 |
| 4 | 4 | 90 | 80 | 160 |
| 5 | 5 | 80 | 100 | 180 |
| 6 | 3 | 60 | 90 | 150 |
| 7 | 2 | 50 | 110 | 170 |
| 8 | 1 | 70 | 120 | 140 |
| 9 | 5 | 90 | 100 | 160 |
| Пример | 6 | 50 | 120 | 140 |
| Вариант | III | II | I | III |
Указания:. Форма сечения представлена на рис.4.2.1. Полюс р назначьте в точке сечения с максимальными координатами X и Y.
Решение: Определим положение центра тяжести сечения (относительно оси
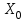) и осевые моменты инерции сечения (см. рис. 5.2.1). Пример такого расчета представлен в задаче 4.2.В нашем примере (расчет не приводим) получено:
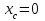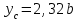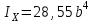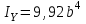, , , . Рис. 5.2.1.
Определим положение нейтральной линии по координатам ее пересечения с осями X и Y :
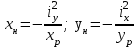,где
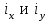- радиусы инерции сечения, 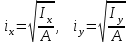.Произведя расчет, получаем
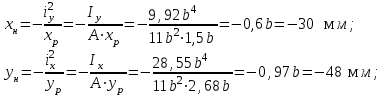
и, отложив эти координаты на оси X и Y, проводим через них нейтральную линию.
Выполним подбор допускаемой нагрузки из условия
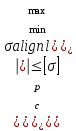.Максимальные и минимальные напряжения в наиболее удаленных от нейтральной линии точках сечения (это точка А, совпадающая с полюсом р и точка В) определим по формулам:
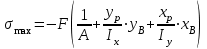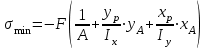; .Произведем расчет:
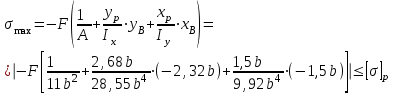
откуда
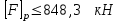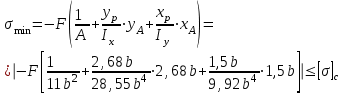
; откуда
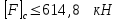.Окончательно принимаем
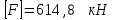.Задача 5.3. Изгиб с кручением
Условие задачи: На валу круглого сечения, вращающемся с угловой частотой
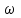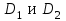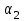, расположены два шкива ременной передачи диаметрами , через которые передается мощность NЭД. Вал закреплен в подшипниковых опорах A и B. Ветви шкива 1 расположены под углом , а шкива 2 - под углом к горизонтали. Требуется: Подобрать диаметра вала по III теории прочности при заданном
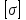.Указания:. Опору А расположите в начале координат, опору В на координате
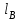, шкивы 1 и 2 соответственно на координатах 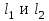.Решение: Определим момент
, действующий на участке вала между шкивами 1 и 2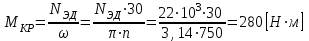 и построим эпюру крутящих моментов.
Определим усилия
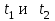в ремённой передаче: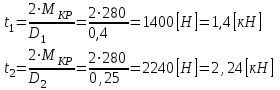 Опорные реакции, необходимые для построения эпюр, определим из уравнений статики:
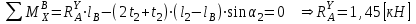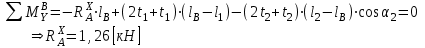; .и строим эпюры изгибающих моментов
.Затем строим эпюру суммарного изгибающего момента
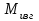, являющегося векторной суммой моментов , т.е. 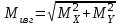.| Исходные данные к задаче 5.3 блица 5.2.2. | Таблица 5.3 | [] МПа | 240 | 220 | 180 | 240 | 160 | 200 | 220 | 180 | 200 | 160 | 160 | I |
| n об/мин | 1500 | 1500 | 1000 | 750 | 1250 | 500 | 750 | 1500 | 1250 | 1000 | 750 | III | ||
| NЭД кВт | 22 | 10 | 16 | 24 | 12 | 20 | 28 | 14 | 26 | 18 | 22 | III | ||
| lВ м | 3,3 | 2,7 | 3,2 | 2,9 | 2,5 | 3,1 | 3,4 | 2,6 | 2,8 | 3,0 | 4,0 | II | ||
| 2 град | 90 | 75 | 60 | 60 | 75 | 60 | 75 | 90 | 60 | 75 | 60 | III | ||
| D2 м | 0,3 | 0,2 | 0,25 | 0,15 | 0,35 | 0,15 | 0,3 | 0,25 | 0,2 | 0,35 | 0,25 | I | ||
| l2 м | 3,6 | 4,2 | 3,0 | 4,8 | 4,0 | 3,8 | 4,6 | 3,4 | 4,4 | 3,8 | 5,0 | I | ||
| 1 град | 15 | 15 | 30 | 0 | 30 | 0 | 15 | 30 | 30 | 15 | 0 | II | ||
| D1 м | 0,55 | 0,4 | 0,5 | 0,6 | 0,4 | 0,45 | 0,55 | 0,6 | 0,45 | 0,5 | 0,4 | I | ||
| l1 м | 2,1 | 1,5 | 2,4 | 1,7 | 1,9 | 2,3 | 1,6 | 2,0 | 2,2 | 1,8 | 2,0 | II | ||
| Дан-ные | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 | Пр. | Вар. |
Рис. 5.3.1.
По эпюре
определяем опасное сечение вала по максимальному изгибающему моменту 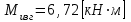.Произведем подбор сечения вала по условию прочности:
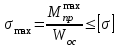,где
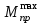- приведенный момент, по III теории прочности 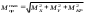; 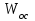- осевой момент сопротивления сечения,для круглого сечения
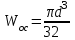.Вычислим диаметр:
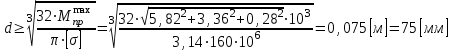
Принимаем d=80 мм.
Тема 6. Напряженное состояние
Задача 6.1. Плоское напряженное состояние
Условие задачи: На грани кубика действует нормальное напряжение по двум взаимно перпендикулярным направлениям, а также касательные напряжения.
Требуется: Найти главные напряжения в направлении главных площадок, относительные деформации, относительное изменение объема и удельную потенциальную энергию деформации.
Исходные данные к задаче 6.1
Таблица 6.1
| Данные | 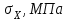 | 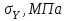 | 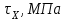 | Материал |
| 0 | 70 | 80 | 30 | бронза |
| 1 | -50 | -100 | -50 | латунь |
| 2 | 80 | -120 | -60 | бронза |
| 3 | -60 | 90 | 40 | сталь |
| 4 | 100 | -110 | 70 | сталь |
| 5 | -100 | 120 | -30 | латунь |
| 6 | 50 | -90 | -70 | сталь |
| 7 | -70 | 110 | 50 | бронза |
| 8 | 60 | -80 | -40 | сталь |
| 9 | -80 | 100 | 60 | латунь |
| Пример | 100 | -50 | -40 | сталь |
| Вариант | III | II | I | II |