Добавлен: 06.11.2023
Просмотров: 110
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
F (см. рис. 3.1).
Требуется: Определить допускаемое количество заклепок из условия прочности на срез и смятие.
Дано: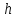
=1,6 м, 
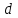=4 м, 
=9 кН, 
=110МПа,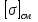 
=330МПа.
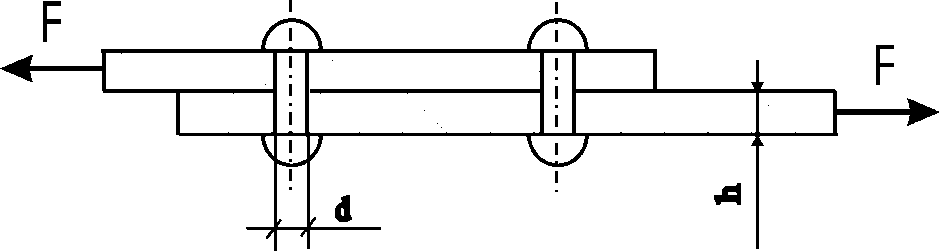
Рис. 3.1.
Указания:. Считать, что усилия между заклепками распределены равномерно, отверстия для заклепок продавлены, прочностные характеристики материала пластин выше, чем заклепок.
Решение: Определим количество заклепок из уравнения расчета на прочность при сдвиге (срезе):
,
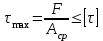где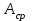
- суммарная площадь среза заклепок.
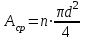, где n – число заклепок.
Откуда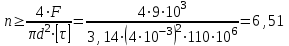
.
Определим количество заклепок из уравнения расчета на прочность при смятии:
,
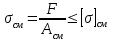где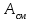
- суммарная площадь смятия заклепок.
.
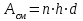Откуда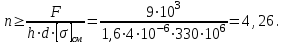
Окончательно принимаем n=7 заклепок.
Тема 4. Изгиб
Задача 4.1. Расчет балки
Условие задачи: На горизонтально расположенную балку, закрепленную на двух шарнирных опорах, действуют активные нагрузки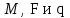
. Материал стержня – ст. 3.
Требуется: Построить эпюры поперечных сил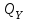
и изгибающих моментов 
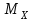и подобрать сечение балки из расчета на прочность.
Исходные данные к задаче 4.1.
Таблица 4.1
Указания:. Шарнирно-неподвижную опору A располагаем на левом конце балки, его же принимаем за начало координат. На соответствующих координатах расположим шарнирно-подвижную опору B и внешние нагрузки, в соответствии с которыми разобьем балку на силовые участки. Силовым участком будет считать ту часть балки, в пределах которой законы изменения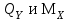
остаются постоянными. Длину каждого участка обозначим через 
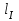. В нашем примере четыре силовых участка.
Решение: Определим опорные реакции из условия равновесия балки:
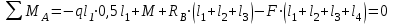
откуда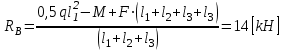
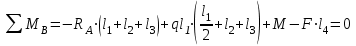
откуда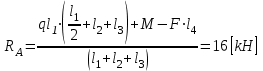
Произведем проверку правильности опорных реакций:
.
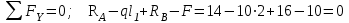Опорные реакции найдены правильно.
Составим уравнения внутренних усилий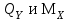 для каждого силового участка балки.
I участок: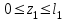
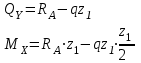
при
;
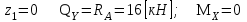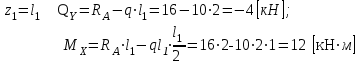
Т.к. поперечная сила
на данном участке поменяла знак, то изгибающий момент 
при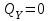 
имеет экстремальное значение. Найдем его.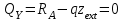 
Отсюда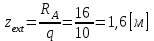
Подставив полученное значение в уравнение изгибающего момента, получим
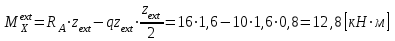
II участок: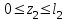
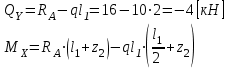
при
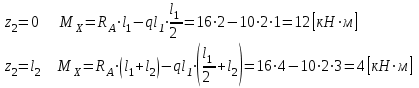
Аналогично производим расчет на III и IV участках, причем здесь сечение удобнее вести справа налево. По результатам расчетов строим эпюры, представленные на рис. 4.1.
По эпюре определяем опасное сечение балки, где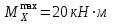 
(по абсолютному значению). Размер сечения (в данном случае № двутавра) вычисляем из условия прочности при изгибе по осевому моменту сопротивления сечения:
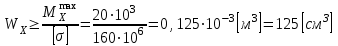
По таблицам сортамента выбираем двутавр № 18, у которого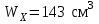
.
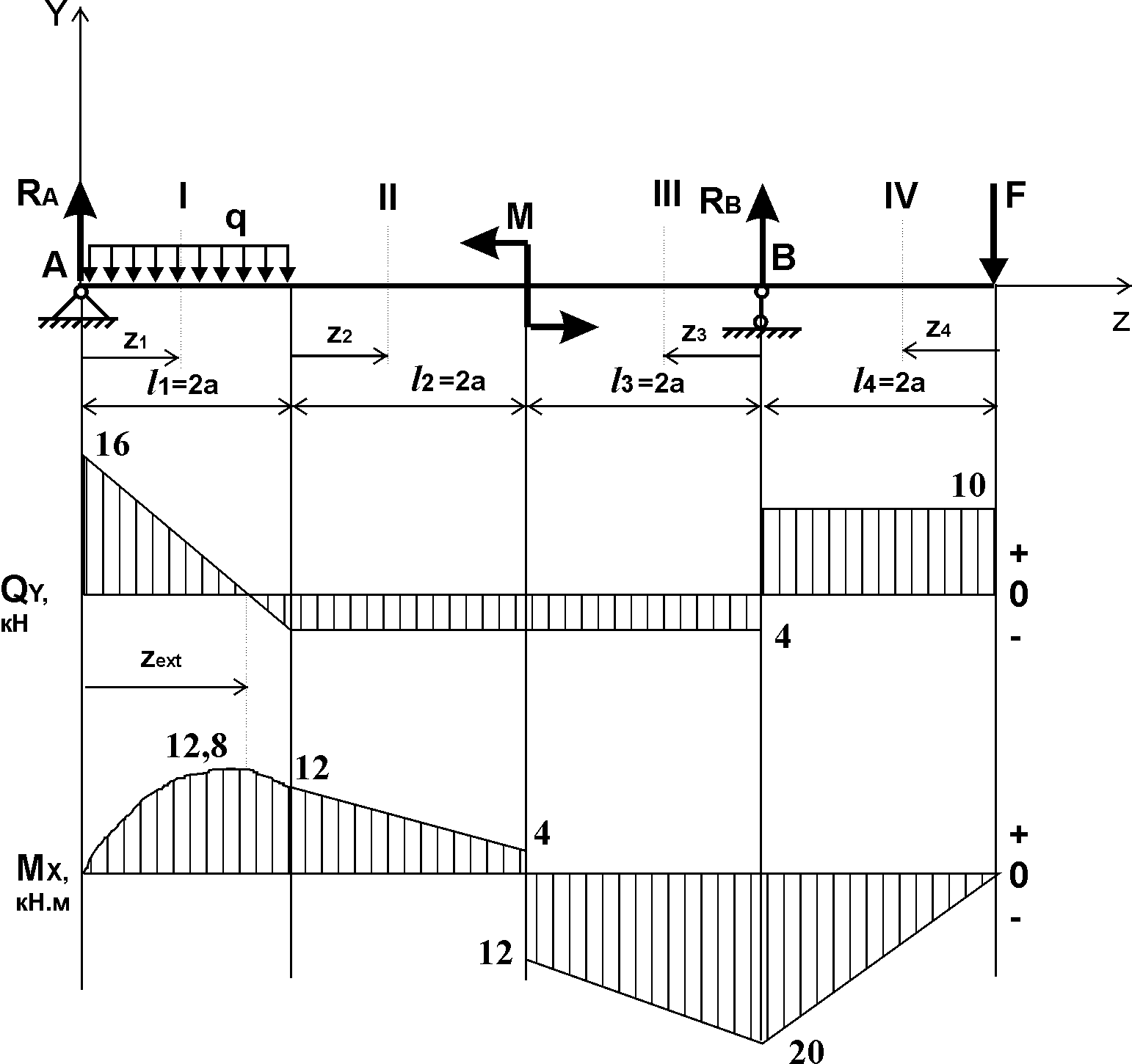
Рис. 4.1.
Задача 4.2. Расчет балки несимметричного сечения
Условие задачи: На горизонтально расположенную балку, жестко закрепленную одним концом, действуют активные нагрузки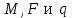
. Сечение стержня несимметрично, материал имеет различные прочностные свойства при растяжении и сжатии.
Требуется: Построить эпюры поперечных сил и изгибающих моментов и подобрать сечение балки из расчета на прочность.
Исходные данные к задаче 4.2
Таблица 4.2
Указания:. Допускаемые напряжения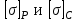
возьмите из табл. 5.2. Жесткую заделку расположите на левом конце балки, там же выберите начало координат. На соответствующих координатах расположите внешние нагрузки, в соответствии с которыми разобьете балку на силовые участки. Длину каждого участка обозначьте через 
.
В нашем примере три силовых участка.
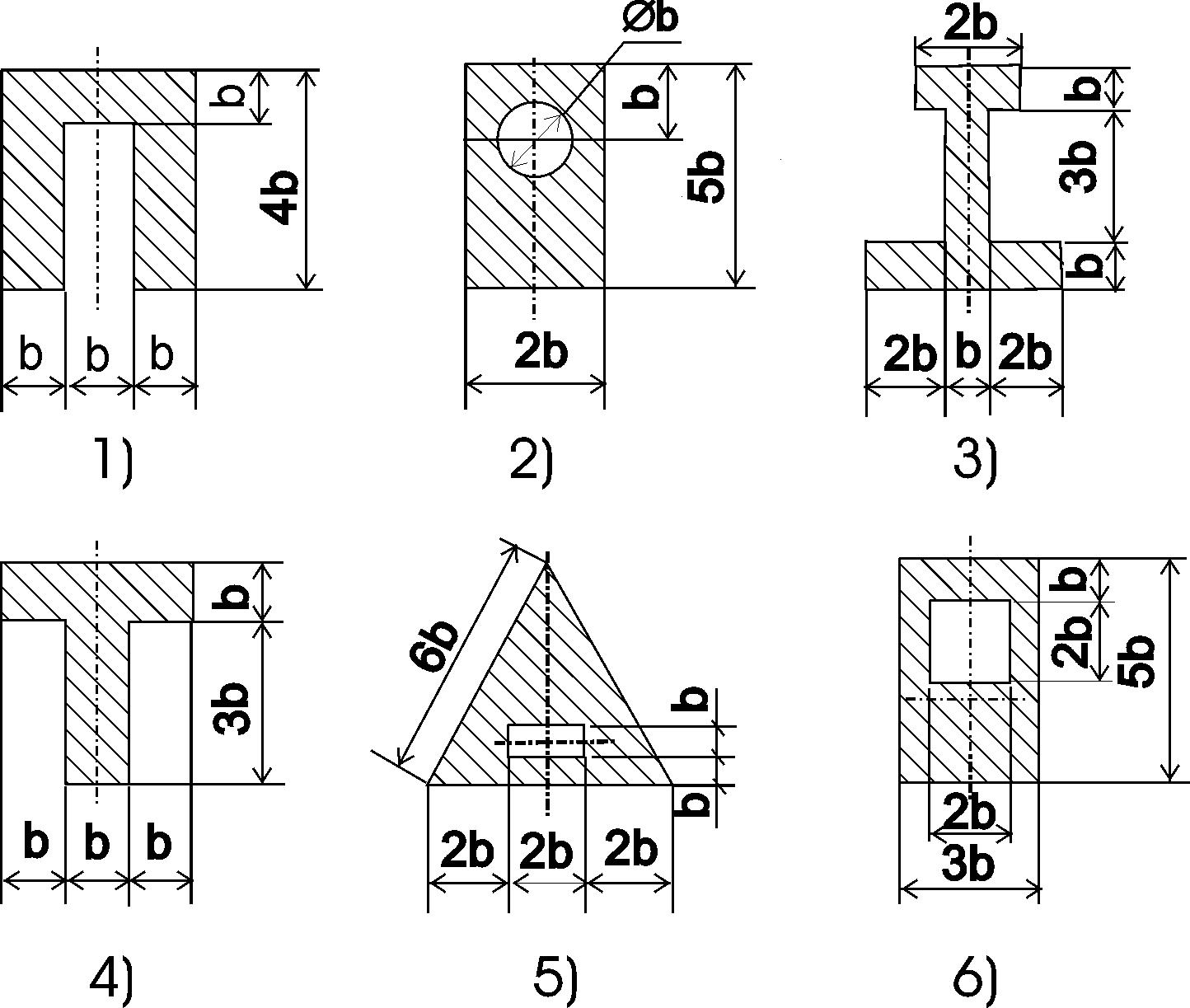
Рис.4.2.1.
Решение: Составим уравнения внутренних усилий
для каждого силового участка балки и построим эпюры, изображенные на рис. 4.2.2. Пример построения эпюр дан в предыдущей задаче.
По эпюре определяем опасное сечение балки, где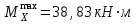 
(по абсолютной величине). Размер сечения вычисляем из условия прочности при изгибе по осевому моменту сопротивления сечения, причем отдельно делаем расчет по растянутым волокнам и отдельно – по сжатым.
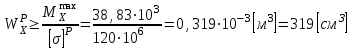
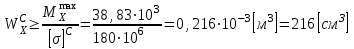
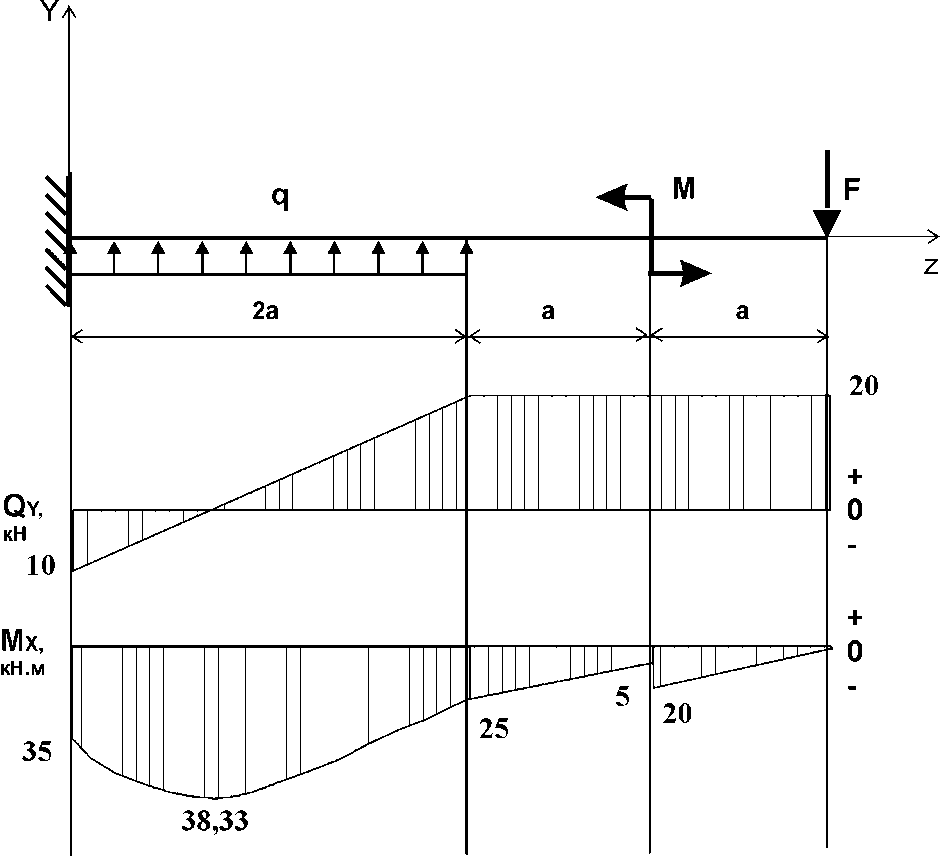
Рис. 4.2.2.
Теперь определим геометрические характеристики сечения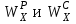
.
Прежде всего, следует определить положение центра тяжести сечения, т.к. через него проходит нейтральная линия. Найдем его по формуле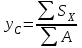
,
где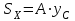
- статический момент, а 
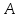- площадь сечения.
Данное сечение можно представить в виде двух фигур:
1 – прямоугольник 3bx5b; 2 – прямоугольный вырез (т.е. отрицательная фигура) 2bx2b. Координаты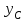
будем откладывать от оси 
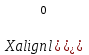(см. рис. 4.2.3.).
Тогда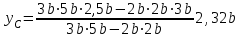
.
Проведем через центр тяжести ось
Требуется: Определить допускаемое количество заклепок из условия прочности на срез и смятие.
Дано:
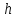=1,6 м, 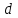=4 м, =9 кН, =110МПа, 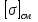=330МПа. Рис. 3.1.
Указания:. Считать, что усилия между заклепками распределены равномерно, отверстия для заклепок продавлены, прочностные характеристики материала пластин выше, чем заклепок.
Решение: Определим количество заклепок из уравнения расчета на прочность при сдвиге (срезе):
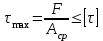,где
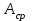- суммарная площадь среза заклепок. 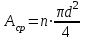, где n – число заклепок.Откуда
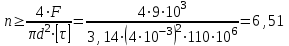.Определим количество заклепок из уравнения расчета на прочность при смятии:
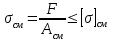,где
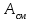- суммарная площадь смятия заклепок. 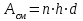.Откуда
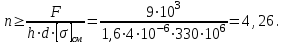
Окончательно принимаем n=7 заклепок.
Тема 4. Изгиб
Задача 4.1. Расчет балки
Условие задачи: На горизонтально расположенную балку, закрепленную на двух шарнирных опорах, действуют активные нагрузки
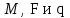. Материал стержня – ст. 3.Требуется: Построить эпюры поперечных сил
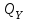и изгибающих моментов 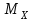и подобрать сечение балки из расчета на прочность.Исходные данные к задаче 4.1.
Таблица 4.1
| Данные | Нагрузки | Координаты | а, м | Сечение | |||||||||
 |  |  |  |  |  |  | | | |||||
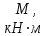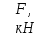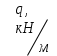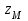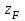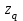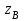| нач. | кон. | | | ||||||||||
| 0 | 5 | -7 | 3 | 5a | a | a | 3a | 5a | 2 | швел. | |||
| 1 | -8 | 12 | -8 | 3a | 1,5a | 1,5a | 3,5a | 3a | 1,5 | двут. | |||
| 2 | -12 | -6 | 6 | 4a | 2a | 3a | 5a | 4a | 2 | швел. | |||
| 3 | 6 | -15 | -5 | 3,5a | a | 2a | 3a | 3,5a | 1,5 | двут. | |||
| 4 | -14 | 13 | -9 | 4,5a | 0,5a | 0 | 2a | 4,5a | 1 | швел. | |||
| 5 | 9 | 8 | -4 | 4a | 2,5a | 4a | 5a | 4a | 1,5 | двут. | |||
| 6 | 7 | -10 | 6 | 5a | 0,5a | 2a | 4a | 5a | 1 | швел. | |||
| 7 | -11 | 14 | 5 | 3,5a | 1,5a | 2,5a | 4,5a | 3,5a | 2 | двут. | |||
| 8 | -13 | 9 | -10 | 3a | 2a | 3a | 4a | 3a | 1 | швел. | |||
| 9 | 10 | -11 | 7 | 4,5a | 2,5a | a | 2a | 4,5a | 1,5 | двут. | |||
| Пр. | 16 | -10 | -10 | 4a | 8a | 0 | 2a | 6a | 1 | двут. | |||
| Вар | II | I | III | III | I | II | II | III | I | III | |||
Указания:. Шарнирно-неподвижную опору A располагаем на левом конце балки, его же принимаем за начало координат. На соответствующих координатах расположим шарнирно-подвижную опору B и внешние нагрузки, в соответствии с которыми разобьем балку на силовые участки. Силовым участком будет считать ту часть балки, в пределах которой законы изменения
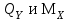остаются постоянными. Длину каждого участка обозначим через 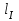. В нашем примере четыре силовых участка.Решение: Определим опорные реакции из условия равновесия балки:
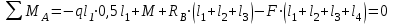
откуда
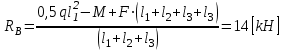
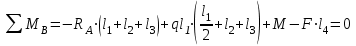
откуда
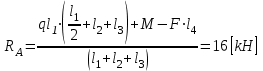
Произведем проверку правильности опорных реакций:
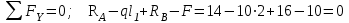.Опорные реакции найдены правильно.
Составим уравнения внутренних усилий
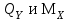для каждого силового участка балки.I участок:
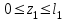
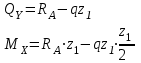
при
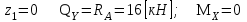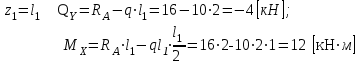
; Т.к. поперечная сила
на данном участке поменяла знак, то изгибающий момент при 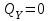имеет экстремальное значение. Найдем его.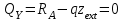 Отсюда
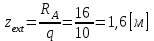
Подставив полученное значение в уравнение изгибающего момента, получим
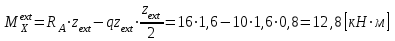
II участок:
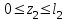
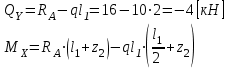
при
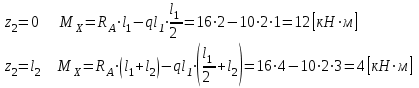
Аналогично производим расчет на III и IV участках, причем здесь сечение удобнее вести справа налево. По результатам расчетов строим эпюры, представленные на рис. 4.1.
По эпюре
определяем опасное сечение балки, где 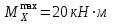(по абсолютному значению). Размер сечения (в данном случае № двутавра) вычисляем из условия прочности при изгибе по осевому моменту сопротивления сечения: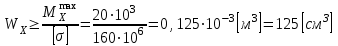 По таблицам сортамента выбираем двутавр № 18, у которого
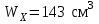. Рис. 4.1.
Задача 4.2. Расчет балки несимметричного сечения
Условие задачи: На горизонтально расположенную балку, жестко закрепленную одним концом, действуют активные нагрузки
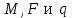. Сечение стержня несимметрично, материал имеет различные прочностные свойства при растяжении и сжатии.Требуется: Построить эпюры поперечных сил
и изгибающих моментов и подобрать сечение балки из расчета на прочность.Исходные данные к задаче 4.2
Таблица 4.2
| Данные | Нагрузки | Координаты | а, м | Сечение (рис.4.2.1) | ||||||
 |  |  |  |  |  нач. | кон. | ||||
| 0 | -15 | 20 | 10 | 3a | 4a | a | 3a | 0,5 | 3 | |
| 1 | 20 | 15 | -15 | a | 2a | 0 | 2a | 1,3 | 2 | |
| 2 | -10 | -30 | 20 | 1,5a | 2,5a | a | 2a | 1,1 | 5 | |
| 3 | 15 | 20 | -20 | a | 3,5a | 0 | a | 0,6 | 1 | |
| 4 | -10 | -15 | -10 | 3a | 2a | 2a | 4a | 0,8 | 3 | |
| 5 | 15 | -25 | 15 | a | 4a | 0 | 2a | 1,4 | 4 | |
| 6 | -20 | 15 | 10 | 1,5a | 2,5a | a | 2a | 1,0 | 2 | |
| 7 | 15 | 30 | -20 | a | 4a | 0 | a | 1,2 | 1 | |
| 8 | -20 | -20 | 10 | 3a | 3,5a | 2a | 4a | 0,7 | 5 | |
| 9 | 10 | 25 | -15 | 1,5a | 2a | a | 3a | 0,9 | 4 | |
| Пр. | 15 | -15 | 20 | 3a | 4a | 0 | 2a | 1,0 | 6 | |
| Вар | II | I | III | III | I | II | II | I | III | |
Указания:. Допускаемые напряжения
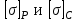возьмите из табл. 5.2. Жесткую заделку расположите на левом конце балки, там же выберите начало координат. На соответствующих координатах расположите внешние нагрузки, в соответствии с которыми разобьете балку на силовые участки. Длину каждого участка обозначьте через . В нашем примере три силовых участка.
Рис.4.2.1.
Решение: Составим уравнения внутренних усилий
для каждого силового участка балки и построим эпюры, изображенные на рис. 4.2.2. Пример построения эпюр дан в предыдущей задаче.По эпюре
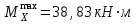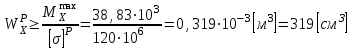
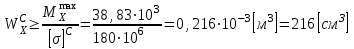
определяем опасное сечение балки, где (по абсолютной величине). Размер сечения вычисляем из условия прочности при изгибе по осевому моменту сопротивления сечения, причем отдельно делаем расчет по растянутым волокнам и отдельно – по сжатым. Рис. 4.2.2.
Теперь определим геометрические характеристики сечения
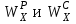.Прежде всего, следует определить положение центра тяжести сечения, т.к. через него проходит нейтральная линия. Найдем его по формуле
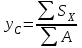, где
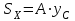- статический момент, а 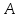- площадь сечения.Данное сечение можно представить в виде двух фигур:
1 – прямоугольник 3bx5b; 2 – прямоугольный вырез (т.е. отрицательная фигура) 2bx2b. Координаты
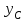будем откладывать от оси 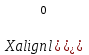(см. рис. 4.2.3.).Тогда
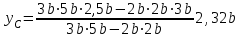.Проведем через центр тяжести ось