Добавлен: 06.11.2023
Просмотров: 111
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
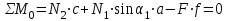 . (1.3.1)
. (1.3.1)Уравнения статики
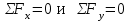 не составляем, поскольку они содержат не интересующие нас реакции в опоре О.
не составляем, поскольку они содержат не интересующие нас реакции в опоре О.Неизвестных усилий в стержневой системе больше, чем уравнений статики, на единицу, следовательно, система один раз статически неопределима. Составим одно дополнительное уравнение совместности деформаций стержней, которое получим из плана перемещений (см. рис. 1.3.2). В результате деформации стержней от действия силы
 абсолютно жесткий стержень повернется на некоторый угол, и шарниры
абсолютно жесткий стержень повернется на некоторый угол, и шарниры 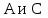 займут новое положение
займут новое положение 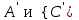 .
.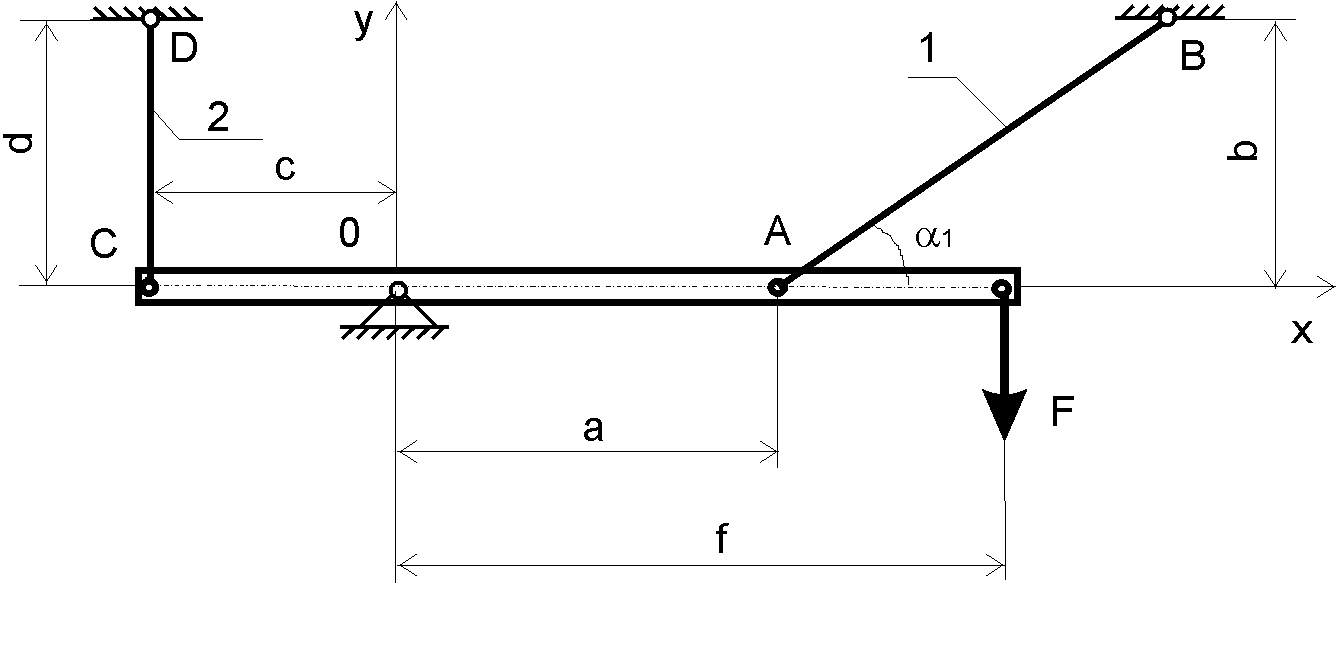
Рис. 1.3.1
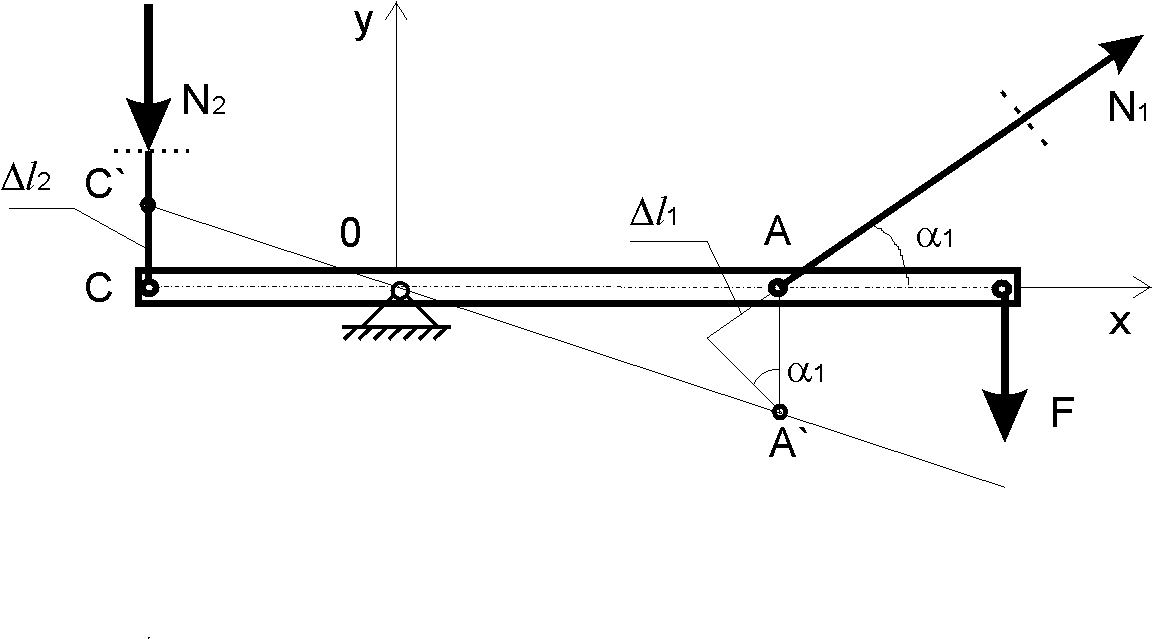
Рис. 1.3.2
Из подобия треугольников
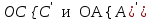 выразим
выразим 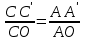 ,
,где
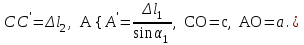
Получаем
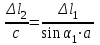 ,
,где
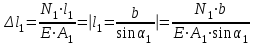 ,
,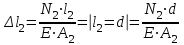 .
.Тогда
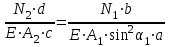 .
.Отсюда
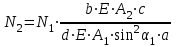 .
.Подставив в полученное уравнение числовые значения, получим
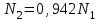 . (1.3.2)
. (1.3.2)Получены уравнения (1.3.1) и (1.3.2) для раскрытия статической неопределимости системы. Составим уравнения расчета стержней 1 и 2 на прочность:
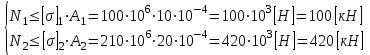 (1.3.3)
(1.3.3)Определим силу
 , при которой будет соблюдено и условие статики по уравнениям (1.3.1, 1.3.2), и условие прочности (1.3.3).
, при которой будет соблюдено и условие статики по уравнениям (1.3.1, 1.3.2), и условие прочности (1.3.3).Пусть
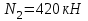
,
тогда из уравнения (1.3.2)
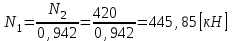 .
.Но это противоречит условию (1.3.3).
Примем
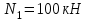 ,
,Тогда
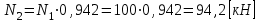 , что согласуется с условием (1.3.3).
, что согласуется с условием (1.3.3).Подставляя полученные значения
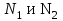 в уравнение (1.3.1), найдем
в уравнение (1.3.1), найдем 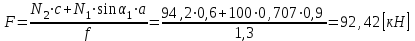 .
.Задача 2.1. Расчет вала
Условие задачи: К стальному валу, состоящему из 4-х участков длиной
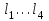 , приложено четыре сосредоточенных момента
, приложено четыре сосредоточенных момента 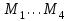 .
.Требуется Построить эпюру крутящих моментов
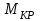 , подобрать диаметр вала из расчета на прочность, построить эпюру максимальных касательных напряжений
, подобрать диаметр вала из расчета на прочность, построить эпюру максимальных касательных напряжений 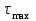 , построить эпюру углов закручивания
, построить эпюру углов закручивания 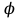 вала и определить наибольший относительный угол закручивания вала.
вала и определить наибольший относительный угол закручивания вала.Дано:
 =1,1 м,
=1,1 м,  =0,6 м,
=0,6 м,  =0,9 м,
=0,9 м, 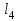 =0,4 м,
=0,4 м, 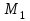 = -4,5
= -4,5 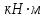 ,
, 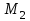 = -2,6
= -2,6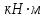 ,
, 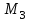 =4,7
=4,7 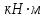 ,
, 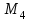 = -2,0
= -2,0 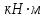 .
.Указання: Вычертим схему вала в соответствии с табл. 2.1. и рис. 2.1. Знаки моментов в таблице означают: плюс – момент действует против часовой стрелки относительно оси Z, минус – по часовой стрелке (смотри навстречу оси Z). В дальнейшем значения моментов принимать по абсолютной величине. Участки нумеруем от опоры.
Допускаемое касательное напряжение
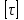 для стали примем равным 100 МПа.
для стали примем равным 100 МПа.Решение: Определим методом сечений значения крутящих моментов на каждом силовом участке, начиная от свободного конца вала. Крутящий момент равен алгебраической сумме внешних моментов, действующих на вал по одну сторону от сечения.
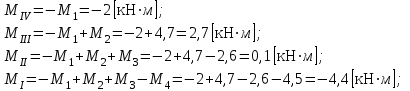
Подберем сечение вала из расчета на прочности при кручении по полярному моменту сопротивления сечения:
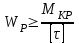
Так как для круглого сечения
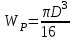 , то
, то 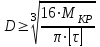 .
.Подставим в уравнение
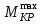 по абсолютному значению из эпюры крутящих моментов и получим
по абсолютному значению из эпюры крутящих моментов и получим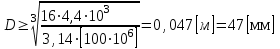
Принимаем
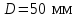 .
.Определим угол закручивания каждого участка вала по формуле
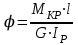 ,
,где
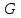 – модуль упругости 2-го рода, Па;
– модуль упругости 2-го рода, Па;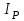 - полярный момент инерции сечения (для круглого сечения
- полярный момент инерции сечения (для круглого сечения 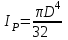 ),
), 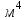 .
.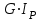 - жесткость сечения при кручении,
- жесткость сечения при кручении, 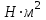 .
.Для данного вала
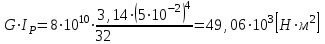
Произведя расчет, получим
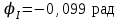 ,
, 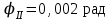 ,
, 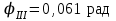 ,
, 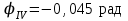 .
.Определим углы закручивания сечений вала, начиная от опоры, где
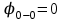
:
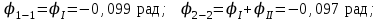
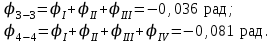
Определим максимальное касательное напряжение на каждом участке по формуле
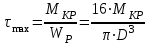 .
.Произведя расчет, получим
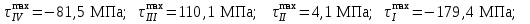 По результатам расчетов строим эпюры
По результатам расчетов строим эпюры 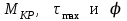 , представленные на рис. 2.1.
, представленные на рис. 2.1.Наибольший относительный угол закручивания определим по формуле
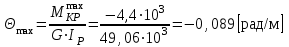
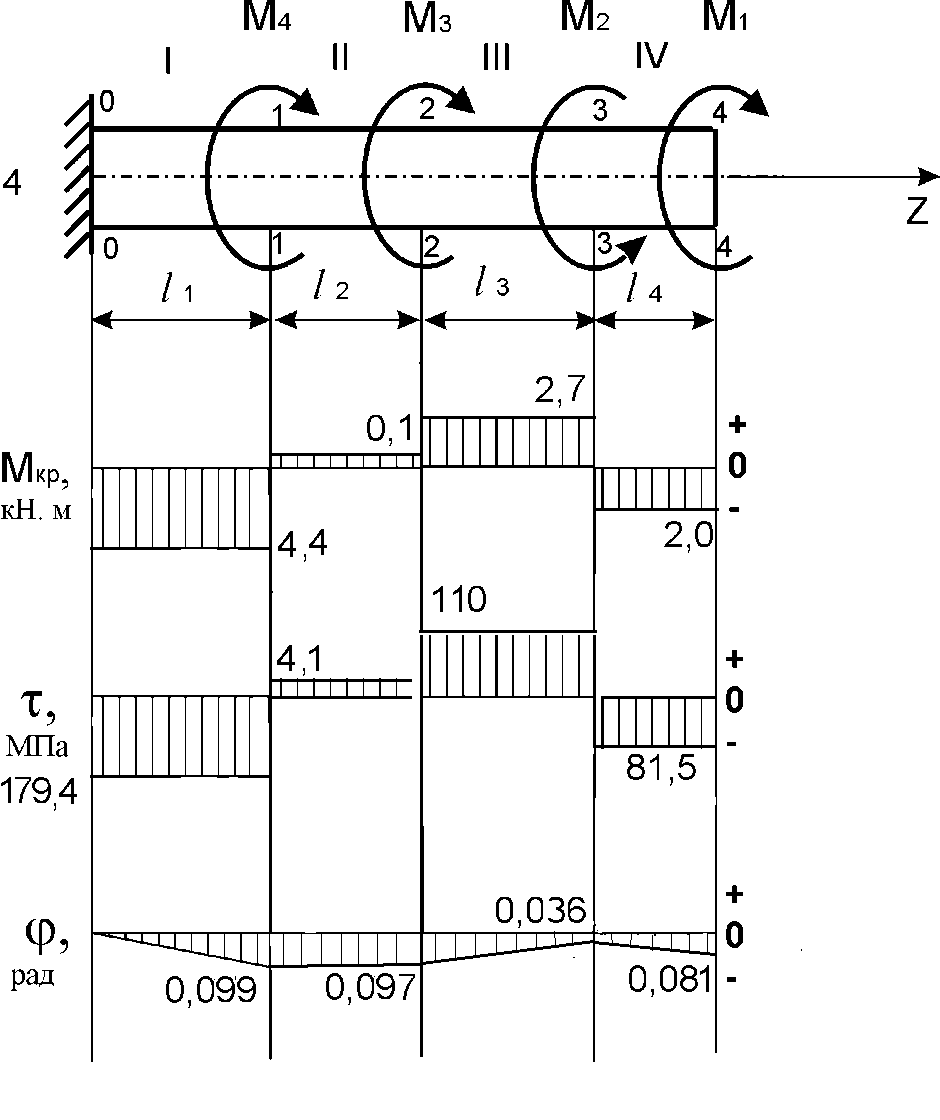
Рис. 2.1.
Задача 2.2. Расчет статически-неопределимого вала
Условие задачи: На статически-неопределимый вал, жестко закрепленный с обоих концов, действует момент М, расположенный на координате
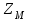 .
.Требуется: Определить опорные реакции, подобрать поперечные размеры вала из расчета на прочность, построить эпюры крутящих моментов, касательных напряжений и углов закручивания.
Дано:
 =0,8 м,
=0,8 м,  =0,9 м,
=0,9 м,  =1,1 м,
=1,1 м, 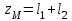 ,
, 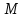 = 1,0
= 1,0  ,
, 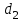 = 1,5
= 1,5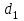 ,
, 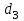 =0,5
=0,5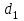 .
.Указания:. Вычертите схему вала в соответствии с исходными данными из табл. 2.2. Начало координат расположите на левом конце вала.
Решение: Данный вал является статически-неопределимым, так как опорных реакций
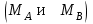
у него больше, чем уравнений статики
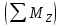 на единицу. Следовательно, для раскрытия статической неопределимости следует составить одно дополнительное уравнение перемещений, а именно, уравнение угла закручивания вала:
на единицу. Следовательно, для раскрытия статической неопределимости следует составить одно дополнительное уравнение перемещений, а именно, уравнение угла закручивания вала: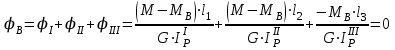 ,
,где
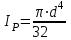 .
.Так как по условию задачи
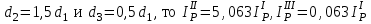
Тогда, решая уравнение, получим
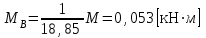 .
.Статическая неопределимость раскрыта. Крутящие моменты на каждом силовом участке найдем методом сечений:
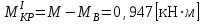 ,
, 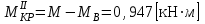 ,
,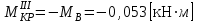 .
.Подбор сечения произведем по уравнению расчета на прочность при кручении:
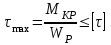 , где
, где 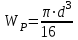 .
.Потенциально опасными в нашем случае являются I и III участки.
Сделаем расчеты на прочность для этих участков:
на I участке
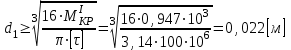 ;
;на III участке
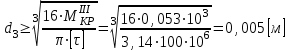 .
.Принимаем
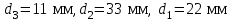 , что не противоречит условиям прочности для всех участков.
, что не противоречит условиям прочности для всех участков.Определим максимальные напряжения и углы закручивания на I участке:
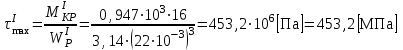 ,
,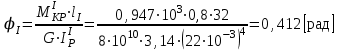 .
.Аналогично произведем расчет
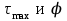 на остальных участках:
на остальных участках: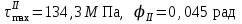 ,
,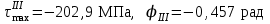 .
.По полученным значениям строим эпюры, представленные на рис.2.2.
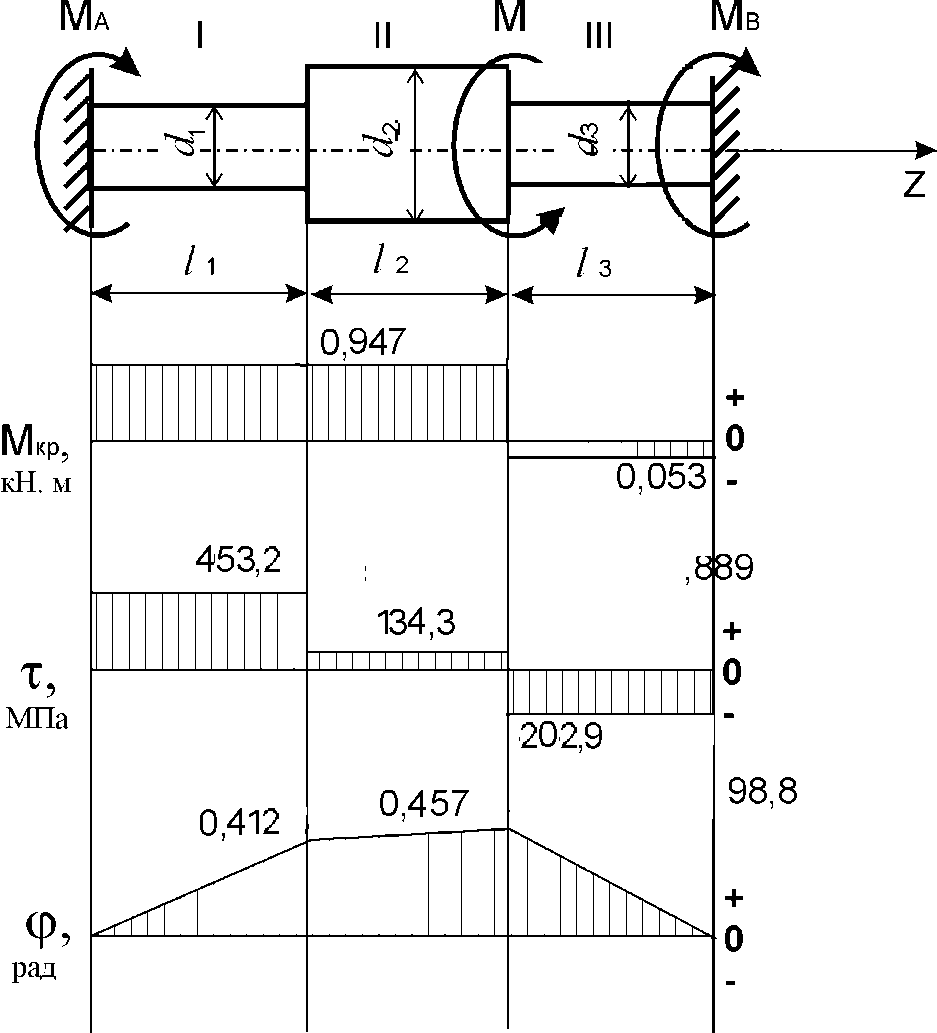
Рис. 2.2
Задача 3.1. Расчет заклепочного соединения
Условие задачи: К пластинам толщиной h, имеющим заклепочное соединение, приложены растягивающие усилия