Добавлен: 06.11.2023
Просмотров: 108
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
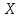и построим эпюры нормальных напряжений 
. В данном случае сечение расположено нерационально, т.к. 
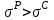, что не согласуется с исходными данными, по которым 
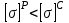. В таком случае сечение переворачиваем (см. рис. 4.2.4).Определим осевой момент инерции сечения
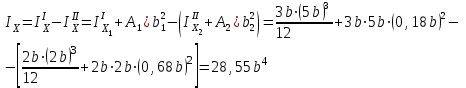Теперь определим осевые моменты сопротивления сечения и для растянутых и для сжатых волокон:
, 
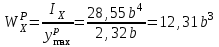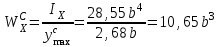.Подберем размеры сечения:
-
по растянутым волокнам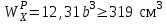
, откуда
;-
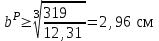по сжатым волокнам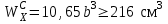
, откуда
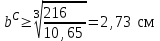.Выбираем большее значение и принимаем
.
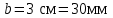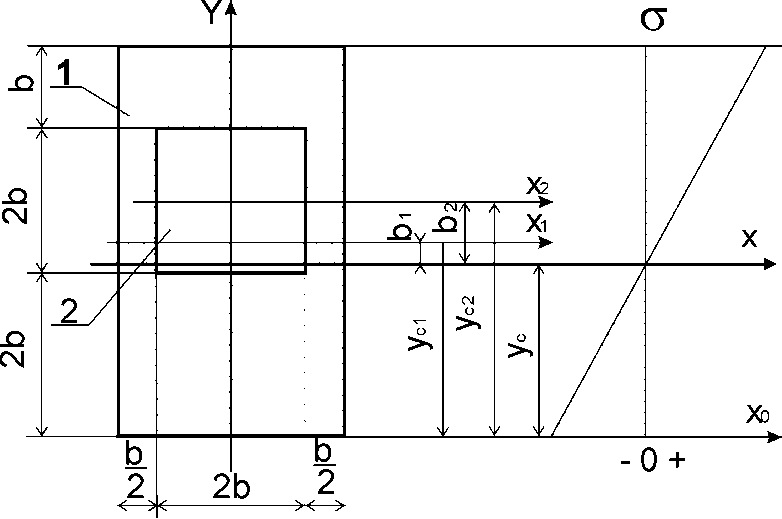
Рис.4.2.3.
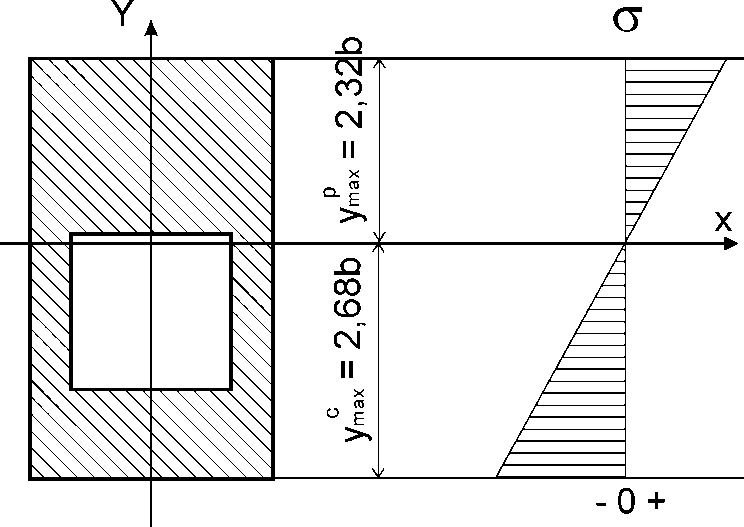
Рис. 4.2.4.
Задача 4.3. Расчет статический-неопределимой балки
Условие задачи: На статически-неопределимую балку, имеющую две опоры: жесткую заделку и шарнирно-подвижную опору, действуют внешние нагрузки: сила F и распределенная нагрузка q.
Требуется: Определить опорные реакции, построить эпюры поперечных сил, изгибающих моментов и линейных перемещений.
Исходные данные к задаче 4.3.
Таблица 4.3
| Данные |  |  |  |  |  |  | |||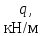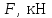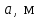
| нач | кон | ||||||||
| 0 | 10 | 0 | 2a | 15 | a | 2a | 1 | ||
| 1 | -10 | 3a | 4a | 5 | 1,5a | 3a | 1,5 | ||
| 2 | -20 | 0 | 2a | 10 | 3,5a | 2a | 2 | ||
| 3 | 20 | 0 | 3a | 20 | 4a | 3a | 1,5 | ||
| 4 | -15 | 2a | 4a | -5 | 0,5a | 2a | 2 | ||
| 5 | -20 | 0 | 3a | 10 | 2,5a | 3a | 1 | ||
| 6 | 15 | 2a | 3a | -10 | 4a | 2a | 1,5 | ||
| 7 | 5 | 0 | 3a | 15 | 2,5a | 3a | 2 | ||
| 8 | 20 | 2a | 4a | -15 | a | 2a | 1,5 | ||
| 9 | -5 | 3a | 4a | -20 | 1,5a | 3a | 2 | ||
| Пример | 10 | 0 | 3a | 15 | 3,5a | 3a | 2 | ||
| Вариант | III | I | I | III | II | I | II | ||
Указания:. Вычертим схему балки в соответствии с исходными данными из табл. 4.3. Жесткую заделку расположим на левом конце балки, там же выберем начало координат.
Раскрытие статической неопределимости следует производить методом сил, определение линейных перемещений – методом начальных параметров.
Решение: Данная балка является статически-неопределимой, так как опорных реакций у нее больше, чем уравнений статики на единицу. Следовательно одна опорная реакция "лишняя". За лишнюю связь можно принять, например, реакции
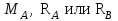, но не 
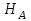, так как без нее балка не сможет сохранять равновесие. Примем за лишнюю связь реактивный момент 
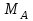.Составим эквивалентную схему балки, отбросив лишнюю связь и заменив ее неизвестным усилием
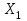.Каноническое уравнение метода сил для один раз статически неопределимой системы имеет вид
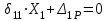, которое для данной системы является уравнением угла поворота балки в начале координат, т.е. в жесткой заделке. Для вычисления его коэффициентов подстроим грузовую 
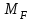(от внешних нагрузок) и единичную 
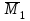(от усилия 
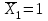) эпюры изгибающих моментов.Затем найдем коэффициенты канонического уравнения способом Верещагина, перемножая соответствующие эпюры. По способу Верещагина произведение эпюр (например
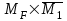) равно площади грузовой эпюры, умноженной на высоту единичной эпюры, взятой под центром тяжести грузовой эпюры.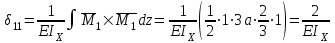
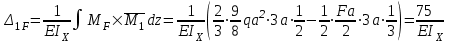
Подставим полученные значения в каноническое уравнение и найдем
:
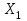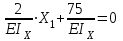, отсюда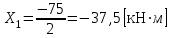 
Статическая неопределимость балки раскрыта.
Отрицательное значение
показывает, что направление этого усилия мы установили неверно и его следует поменять. Таким образом, MA= -X1. Теперь из уравнений статики найдем опорные реакции: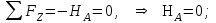
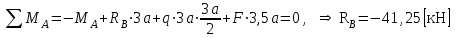
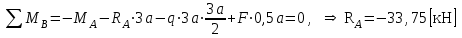
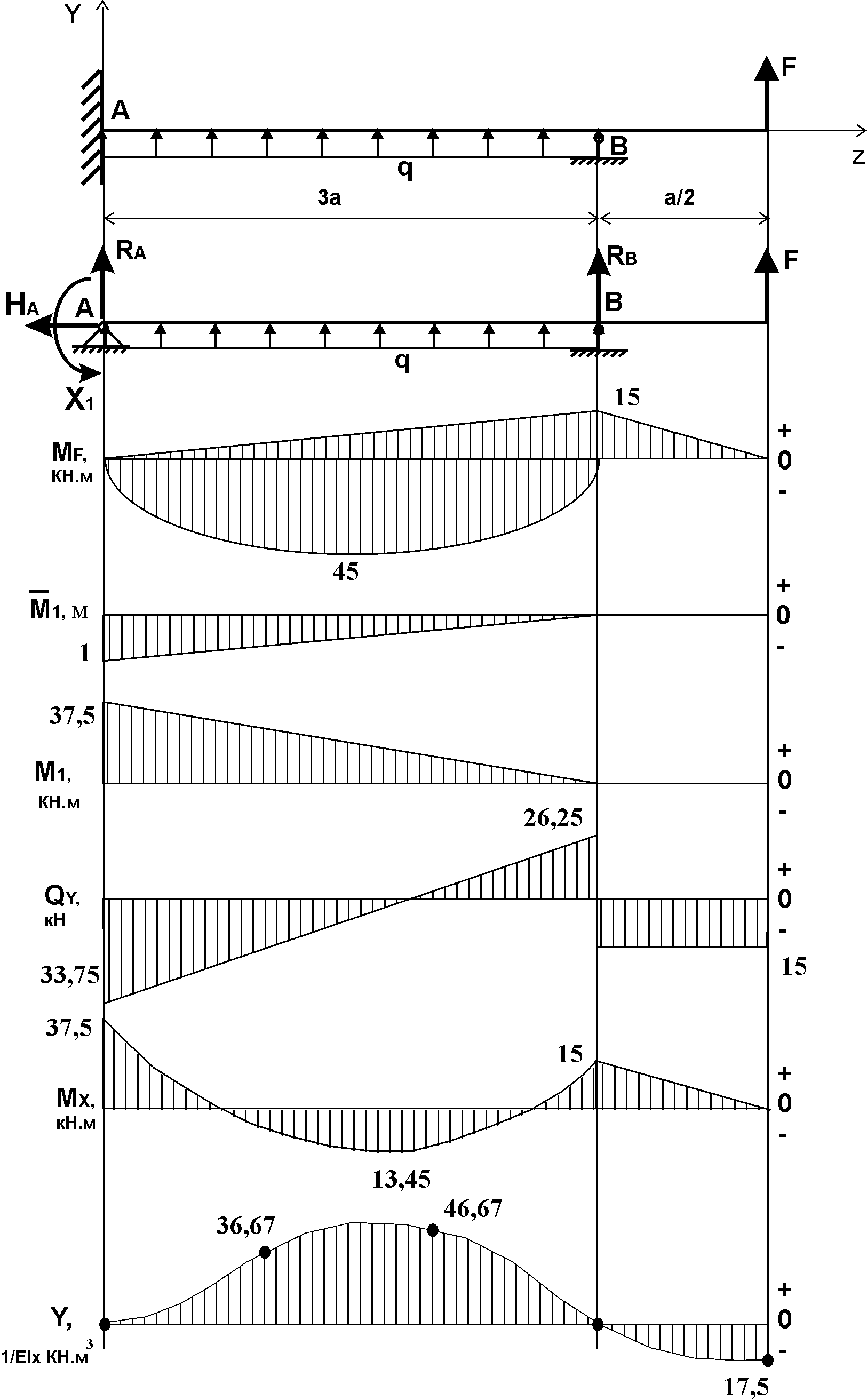
Рис.4.3.
Далее строим эпюры
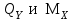(пример построения эпюр смотри в задаче 4.1.).Для построения эпюры линейных перемещений Y (прогибов) требуется определить их значения в 4-5 сечениях балки.
В нашем случае известно, что
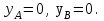Вычислим прогибы на координатах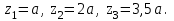 
Уравнения прогибов в этих сечениях по методу начальных параметров имеют вид:
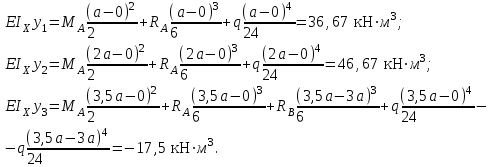По полученным значениям строим эпюру Y.Тема 5. Сложное сопротивление
Задача 5.1. Косой изгиб
Условие задачи: На консольную балку прямоугольного сечения действуют внешние нагрузки, расположенные в разных плоскостях.
Требуется: Подобрать размеры поперечного сечения балки из условия прочности и определить линейное перемещение сечения на конце балки.
Исходные данные к задаче 5.1.
Таблица 5.1
| Данные | Нагрузки | Координаты, м | а, м | [], МПа | Плоско-сть дей-ствия нагрузки | |||||||||
| M, кН м | F, кН | q, кН/м |  | | нач | кон | | | | |||||
| 0 | 15 | 20 | 17 | a | 2a | 0 | a | 0,5 | 160 | M-XOZ F-YOZ q-YOZ | ||||
| 1 | -18 | -15 | -15 | 2a | a | 0 | 2a | 0,7 | 220 | |||||
| 2 | 12 | -22 | -20 | a | 3a | a | 2a | 0,6 | 200 | |||||
| 3 | 20 | 17 | 10 | 3a | 2a | 0 | a | 0,9 | 140 | |||||
| 4 | -10 | 25 | -23 | a | 4a | 0 | 2a | 0,8 | 180 | M-XOZ F-YOZ q-XOZ | ||||
| 5 | 18 | -20 | 17 | 2a | 3a | a | 3a | 0,7 | 220 | |||||
| 6 | -12 | 15 | -20 | 2a | a | 0 | a | 0,5 | 160 | |||||
| 7 | -10 | -25 | 10 | a | 3a | a | 3a | 0,9 | 140 | M-XOZ F-XOZ q-YOZ | ||||
| 8 | 20 | -22 | 23 | 2a | 4a | 0 | 2a | 0,6 | 200 | |||||
| 9 | -15 | 17 | -15 | 2a | A | a | 2a | 0,8 | 180 | |||||
| Пр. | -15 | 15 | -10 | a | 3a | a | 2a | 1,0 | 140 | |||||
| Вар | II | I | III | III | III | II | II | I | III | II | ||||
Указания:. Модуль Юнга принять равным
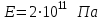.Решение: Схема балки, построеная по исходным данным примера, представлена на рис. 5.1. Эпюры изгибающих моментов
(в силовой плоскости YOZ) и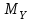 
(в силовой плоскости XOZ) представлены на рис. 5.2. Пример построения эпюр изложен в задаче 4.1.Определяем опасное сечение балки, где
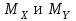имеют максимальные значения: 
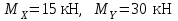. В случае наличия не-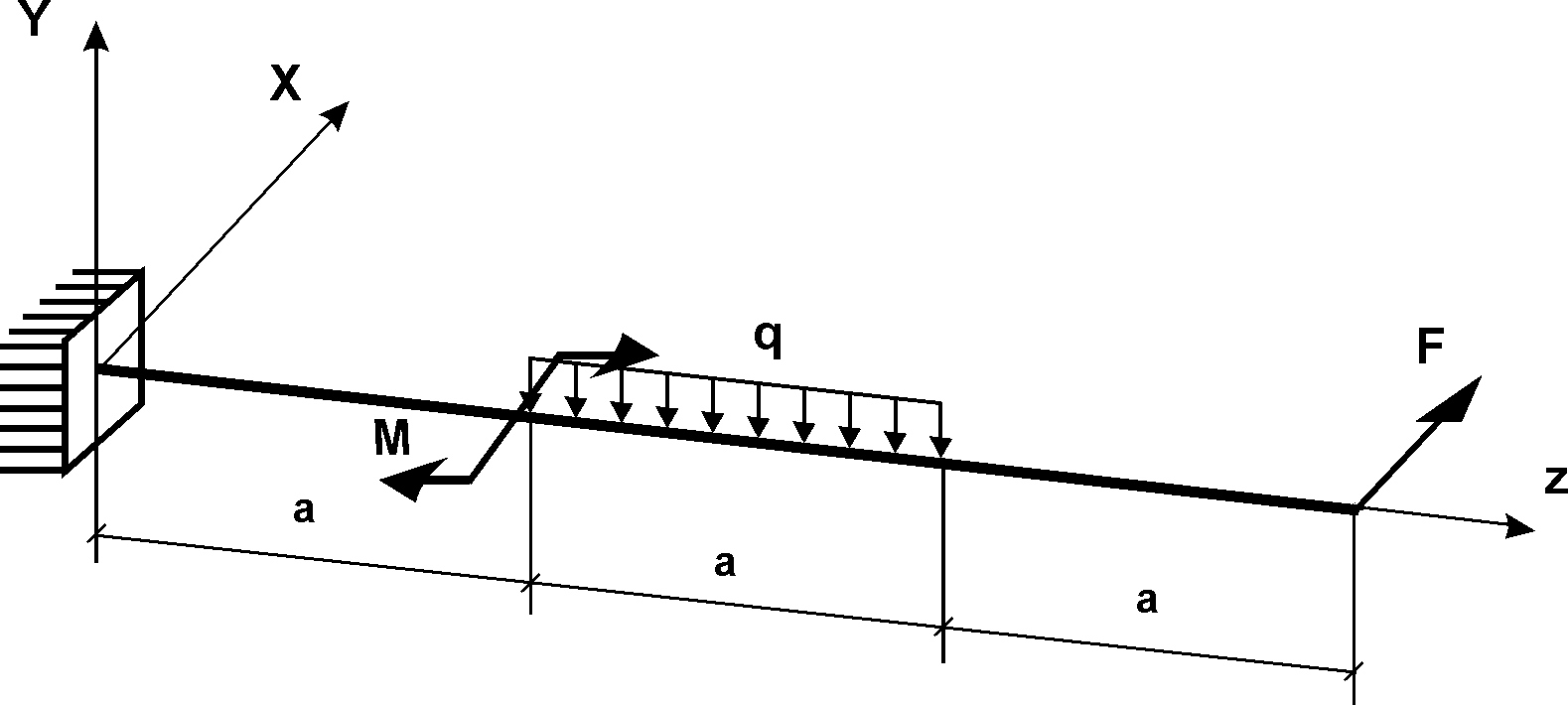
Рис. 5.1.1 Исходная схема балки
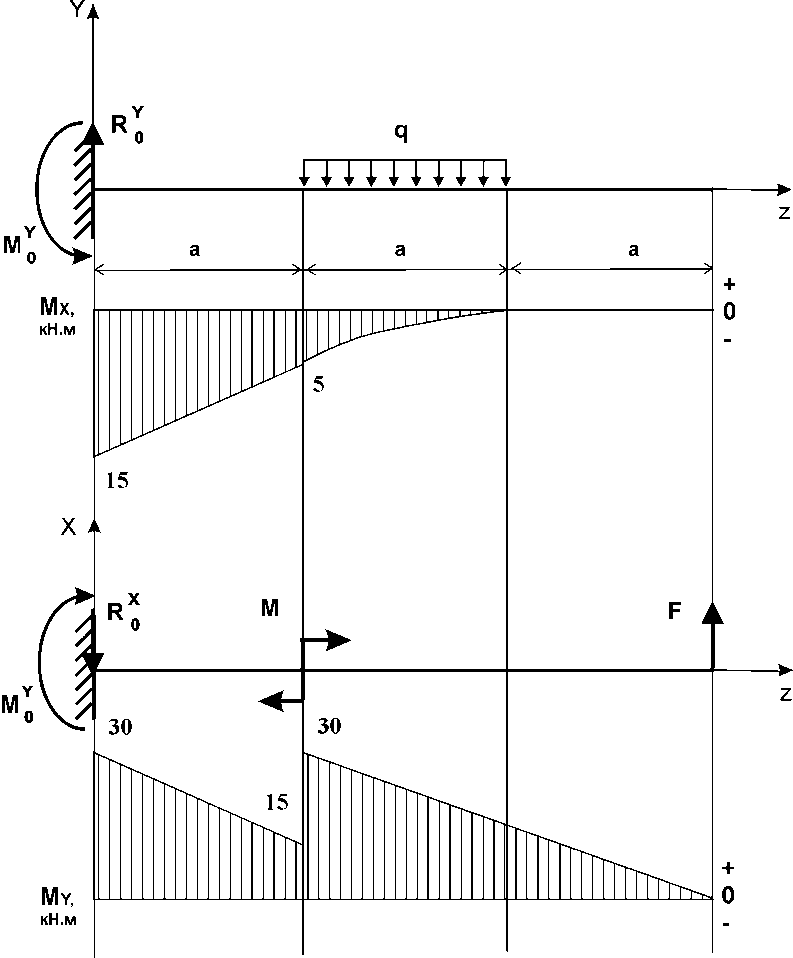
Рис. 5.1.2 Эпюры изгибающих моментов
скольких потенциально опасных сечений необходимо делать расчет на прочность по каждому опасному сечению.
Сечение следует расположить рационально. Так как в нашем случае
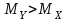, то сечение располагаем так, чтобы соблюдалось условие 
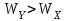. Строим на сечении эпюры напряжений для определения опасной точки сечения (см. пример задачи 4.2).Максимальное напряжение возникает в т.1, где напряжения максимальны:
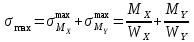,где
;
.
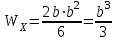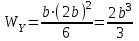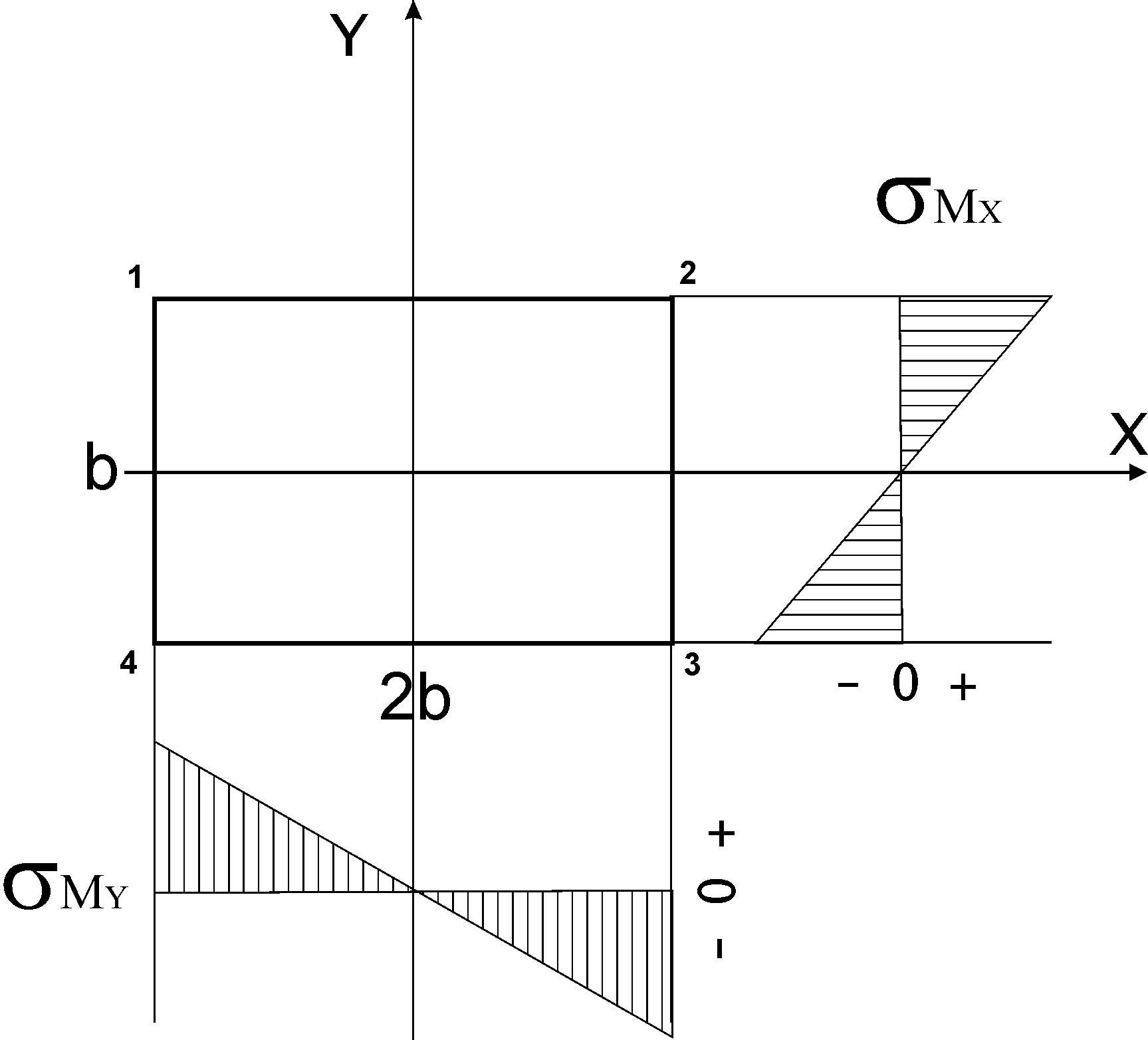
Рис. 5.1.3. Эпюры нормальных напряжений
Определим размер b из условия прочности:
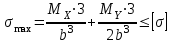, откуда 
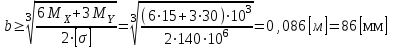.Принимаем b=90 мм.
Определим перемещение конца балки (т. А) по формуле
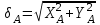,где
