Файл: Учебнометодическое пособие для студентов высших учебных заведений.doc

6.2. Схемы для оценки погрешностей при измерении биений

При анализе составляющих погрешностей измерения радиального и торцового биений могут быть полезны схемы, позволяющие отобразить механизм появления погрешности и вывести аналитические зависимости для оценки значений этих погрешностей. Примером очевидной причины возникновения погрешностей является наклон линии измерения по отношению к ее идеальному направлению (рис. 6.1). В итоге возникает инструментальная составляющая погрешности (в приборах с фиксированным направлением линии измерения) или субъективная составляющая (при установке линии измерения на глаз). Как показывает опыт измерений, отклонения углов от номинального положения в последнем случае не превышает значений (2…3)°.

При измерении радиального и торцового биений погрешности из-за неизменного (постоянного) несовпадения линии измерения с номинальным направлением практически всегда будут пренебрежимо малы из-за малости углов наклона линии измерения и небольших измерительных перемещений. Более опасной является ситуация, когда направление линии измерения изменяется в процессе измерений (плоскопараллельная или угловая осцилляция линии измерения).



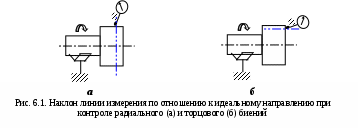
Для случая контроля годной детали наибольшее значение измерительного перемещения можно принять равным допуску биения.

Рассмотрим расчетную схему, которая позволяет оценить погрешности из-за отклонения направления фактической линии измерения (линия АС) от номинального направления линии измерения АВ на угол α (рис. 6.2).



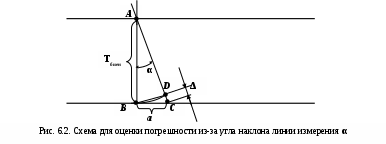
Отрезок АВ (максимальное перемещение измерительного наконечника) принимаем равным допуску биения, поскольку этим допуском ограничено перемещение наконечника при измерении биения годной детали. Результатом наличия угла α. будет дефектное перемещение Δ, равное отрезку DC, который дуга BD отсекает от стороны АС. Проведя хорду BD, стягивающую одноименную дугу, можно приближенно рассчитать значение Δ из треугольника BDC. Треугольник BDC можно принять за прямоугольный треугольник, подобный треугольнику АBC, с прямым углом BDC

---

, и углом DBC = α.

Из треугольника BDC рассчитываем значение Δ, равное отрезку DC:

Δ = DC = BC·sinDBC = a·sinα. (6.1)

Поскольку a = BC = АBtgα, и АB = Т_биен, при Т_биен= Т можно записать:

Δ = Т· tgα · sinα,

что при малости углов α вследствие того, что tgα ≈ sinα, можно представить в виде одной из двух следующих зависимостей:

Δ = Т· tg²α, (6.2)

Δ = Т· sin² α. (6.3)

Увеличение измерительных перемещений при больших значениях допусков биения приведет к росту только абсолютных значений погрешностей, относительные погрешности при неизменных значениях угла α будут одинаковыми.

6.3. Анализ методических погрешностей при контроле радиальных и торцовых биений поверхностей валов

Одной из возможных причин методических погрешностей при измерении биений является некорректная идеализация реального объекта измерений (погрешности из-за несоответствия реального объекта его идеализированной модели, положенной в основу процесса измерения). Здесь следует особо отметить, что рассматривается идеализация не контролируемой поверхности (предмета исследования), а базовых элементов. Базовые элементы по определению задаются как идеальные, поэтому влияние их несоответствий идеалу следует подвергать тщательному анализу. Например, надо анализировать влияние погрешностей формы и расположения базовых шеек вала, если биение задано относительно общей оси двух цилиндрических поверхностей, либо влияние погрешностей, возникающих из-за погрешностей формы центровых отверстий и несовпадения оси центров с рабочей осью (ось, являющаяся конструкторской базой детали) контролируемого вала.

Основные факторы, вызывающие методические погрешности при измерении биений, можно разделить на две группы:

• 
  факторы, вызывающие фиксированное (неизменное) отклонение оси вращения детали от идеального направления, что вызывает постоянное несоответствие реального направления линии измерения биения номинальному;
  
• 
  факторы, вызывающие осцилляцию детали (колебание оси вращения контролируемой детали в процессе измерений из-за плоскопараллельного смещения оси вращения поверхности, либо из-за поворотов реальной оси относительно идеального направления).
  

---

Рассмотрению подлежат модели объектов (рис. 6.3), построенные на основе типовых моделей следующих видов:

• 
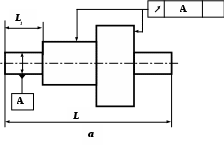
  валы с одной базовой поверхностью (рис. 6.3 а);
  

*


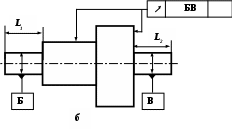
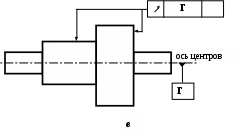
Рис. 6.3. Типовые модели объектов контроля (валов):

а – тип 1 (с одной базовой поверхностью); б – тип 2 (с двумя базовыми поверхностями, совокупность которых определяет конструкторскую базу детали; в – тип 3 (с двумя базовыми поверхностями, совокупность которых определяет технологическую базу детали, т.е. ось центров)

• 
  валы с двумя базовыми поверхностями, совокупность которых определяет конструкторскую базу детали (рис. 6.3 б);
  
• 
  валы с двумя базовыми поверхностями, совокупность которых определяет технологическую базу детали – ось центров (рис. 6.3 в).
  

Реалистические модели, подлежащие исследованию, будут отличаться от идеальных погрешностями формы следующих видов:

• 
  номинально цилиндрические базовые поверхности с овальностью (в том числе расположенные синфазно и экстремально друг относительно друга при наличии двух базовых поверхностей). Экстремальное расположение поперечных сечений базовых поверхностей означает, что в одном продольном сечении вала максимальному радиусу-вектору первой базовой поверхности соответствует минимальный радиус-вектор второй;
  
• 
  номинально цилиндрические базовые поверхности с трехгранной, четырехгранной огранкой, а также с большим числом граней двух базовых поверхностей (в том числе синфазно и экстремально расположенные друг относительно друга);
  
• 
  номинально цилиндрические базовые поверхности с погрешностями формы в продольном сечении, включая конусообразность, седлообразность, бочкообразность и отклонение от прямолинейности оси (изогнутость оси);
  
• 
  детали с центровыми отверстиями, общая ось которых не совпадает с базовой осью (с осью базовой поверхности или с общей осью двух базовых поверхностей).
  

Оценки погрешностей и расчеты их значений выполнены на основе следующих положений:

• 
  каждая из отдельных составляющих погрешности оценивается и рассчитывается в соответствии с принципом суперпозиции погрешностей как независимая (все воздействия, не оговоренные в описании расчета, считаются фиксированными),
  
• 
  числовые значения приняты в соответствии с данными приведенных информационных источников, либо назначены из оговоренных в тексте соображений,
  
• 
  рассматриваются только функционально важные смещения оси вращения контролируемой детали, которые вызывают максимальные методические погрешности, т.е. смещения вдоль линии измерения радиального биения, или смещения в плоскости, проходящей через базовую ось и линию измерения торцового биения,
  
• 
  рассматриваются смещения оси вращения контролируемой детали только при базировании ее в призмах с углом 90^о.
  

---

Для оценки значений возможного смещения осей базовых поверхностей деталей использованы материалы Справочника «Единая система допусков и посадок СЭВ в машиностроении и приборостроении. Контроль деталей», причем ориентировочные оценки базируются на приведенных в справочнике коэффициентах смещений верхних точек реального профиля при его вращении в призме и не соответствуют строго определяемым значениям смещений центров профиля. Однако для оценки ожидаемых методических погрешностей можно воспользоваться этими значениями, поскольку в рамках рассматриваемой задачи фактические смещения осей вращения будут иметь тот же порядок.

В справочнике отмечается, что измерение в призме применяют для деталей, имеющих определенный характер отклонений от круглости, причем предварительно следует определить значение n, то есть число «граней» детали при огранном профиле.

Отклонение от круглости Е _кр рассчитывают из зависимости

Е_кр = Е_А/F_n , (6.4)

где Е_А – размах колебаний периферийной точки сечения при вращении детали в призме;

F_n – коэффициент воспроизведения отклонений от круглости.

Значения коэффициента воспроизведения отклонений от круглости для измерения круглости при вращении детали в призме с углом 90^о и симметричной схеме измерения (направление линии измерения – биссектриса угла призмы) для огранных поверхностей с числом «граней» от 2 до 8 приведены в табл. 6.1.
Таблица 6.1

Коэффициенты воспроизведения при измерении отклонений от круглости

Число граней n	Коэффициент Fn
2	1,00
3	2,00
4	0,41
5	2,00
…………………	…………………..
8	2,41

Приведенные в том же справочнике значения коэффициентов F_n для сечений с большим числом граней (до = 15) не превышают 2,00, кроме случая n = 8, для которого F_n = 2,41. В дополнение следует отметить, что из-за особенностей технологических процессов относительное значение отклонений от круглости при огранке обычно тем меньше, чем больше граней имеет номинально круглая поверхность. Поэтому в нашем исследовании можно практически ограничиться рассмотрением случаев с

---

n ≤ 5.

Поскольку размах колебаний периферийной точки сечения при вращении детали в призме на основании зависимости (6.4) формально можно представить как

Е_А = Е_кр·F_n , (6.5)

с другой стороны, радиальное биение реальной поверхности при вращении детали в призме фактически складывается из погрешностей формы сечения и его изменяющегося эксцентриситета («плавания центра вращения» Е_ц), можно записать

Е_А = Е_кр·F_n , = Е_кр·* Е_ц, (6.6)

где * – знак объединения составляющих, которое в соответствии с видами рассматриваемых величин может быть алгебраическим (функциональное объединение детерминированных величин), геометрическим (стохастическое объединение случайных величин), либо каким-либо иным.

Поскольку Е_А для огранки с числом граней до 15 даже в экстремальном случае составит не более 2,5Е_кр, то для любого из имеющих реальный смысл рассматриваемых случаев можно полагать, что значения Е_ц будут иметь тот же порядок, что и Е_А. Значит, имея в виду малость исследуемых величин, для оценки возможных смещений центра сечения огранной поверхности при ее вращении в призме можно воспользоваться упрощенной зависимостью

Е_ц ≈ Е_А. (6.7)

Априори без измерения отклонений от круглости конкретной поверхности, опираясь на установленный для нее допуск круглости Е_кр = Т_кр, и с учетом приведенных в таблице коэффициентов (исключая случай с восьмигранной огранкой) можно записать

Е_ц ≤ 2Т_кр. (6.8)

Следовательно, при оценке погрешности базирования вала в призме (базовая поверхность – цапфа вала с номинально круглым сечением) можно принять для расчетов, что колебание оси вращения базовой цапфы годного вала в призме не превысит удвоенного значения допуска круглости, назначенного на поверхность данной цапфы.

6.3.1. Методические погрешности из-за плоскопараллельного смещения реальной оси вращения контролируемой поверхности

Причинами возникновения таких погрешностей при базировании детали в одной или двух призмах могут быть отклонения формы базовых поверхностей. Рассмотрим в качестве примера случай, когда у деталей типа 2 (с двумя наружными поверхностями, образующими составную базу) базовые поверхности имеют овальность, трехгранную огранку или огранку с большим числом граней с синфазно расположенными друг относительно друга поперечными сечениями (рис. 6.4).

---