Файл: Интеллектуальные информационные системы и технологии.doc

До недавнего времени наиболее популярным языком реализации
ИИ-систем был ЛИСП, разработанный под руководством Дж. Маккарти в Стэнфорде в начале 60-х годов XX века. Этот язык должен был стать следующим за ФОРТРАНом шагом на пути к автоматизации програм-мирования. К концу 1980-х годов ЛИСП был реализован на всех классах ЭВМ, от персональных до высокопроизводительных вычислительных систем. В настоящее время фирмами США, Японии, Западной Европы выпускаются ЛИСП-машины.

Параллельно разрабатывались другие языки обработки символьной информации (СНОБОЛ, РЕФАЛ). СНОБОЛ стал одной из первых практических реализаций развитой продукционной системы. РЕФАЛ вобрал в себя лучшие черты языков обработки символьной информации.

В начале 1970-х годов появился ПРОЛОГ, разработанный в Марсельском университете. В японском проекте вычислительных систем V поколения ПРОЛОГ был выбран в качестве базового языка для машины вывода. ПРОЛОГ удобен, если число отношений не слишком велико и каждое отношение описывается небольшим числом альтернатив. Механизмы вывода обеспечивают поиск решения на основе перебора альтернатив и декларативного возврата из тупиков. ЛИСП, СНОБОЛ, РЕФАЛ и ПРОЛОГ – языки общего назначения для задач ИИ. Вместе с тем в рамках развития средств автоматизации ПС, ориентированных на знания, были разработаны языки ПЛЭНЕР, КОННАЙВЕР, основанные на программировании поисковых задач и сыгравшие важную роль в эволюции основных языков ИИ. Эти языки функционируют в ЛИСП-среде, реализуют представление данных в виде поисковых структур, развитые методы сопоставления образцов, поиск с возвратами и вызов процедур по образцу.

Тогда же в ИИ сформировались концепции представления знаний на основе семантических сетей и фреймов. Характерными чертами раз-работанных языков KRL, FRL были двухуровневое представление данных (абстрактная модель предметной области в виде иерархии множеств понятий и конкретная модель ситуаций как совокупность взаимосвязанных экземпляров этих понятий); представление связей между понятиями и закономерностей предметной области в виде присоединенных процедур; семантический подход к сопоставлению образцов и поиску по образцу.

Одним из распространенных ЯПЗ стал OPS5 (Official Production Systems), который в начале 1980-х годов претендовал на роль языка стандарта в области представления знаний для ЭС. OPS5 – один из самых многочисленных на сегодняшний день ЯПЗ для ЭС, поддерживающий продукционный подход к представлению знаний. Модуль вывода решений в OPS5-системе включает в себя три блока:

---

отождествления, где осуществляется поиск подходящих правил;

выбора исполняемого правила из конфликтного множества правил;

исполнителя выбранного правила.

В OPS5 поддерживается единственная стратегия вывода решений – вывод, управляемый целями (обратный вывод).

В общем случае к ЯПЗ предъявляются следующие требования:

наличие простых и мощных средств представления сложно-структурированных и взаимосвязанных объектов;

возможность отображения описаний объектов на разные виды памяти компьютера;

наличие гибких средств управления выводом, учитывающих не-обходимость структурирования правил работы решателя;

«прозрачность» системных механизмов для программиста, пред-полагающая возможность их доопределения и переопределения на уровне входного языка;

возможность эффективной реализации.

Следующим этапом в развитии инструментальных средств стала ориентация на среды поддержки разработок ИИ-систем. Примерами инструментальных пакетов и систем оболочек служат EXSYS, GURU, однако наиболее распространенными являются ART, KEE, J2.

В середине 1980-х годов система ART была одной из самых современных интегрированных сред, поддерживающих технологию проектирования систем, основанных на правилах. ART является пакетом разработчика и объединяет два главных формализма представления знаний: правила для процедурных знаний и фреймоподобные структуры для декларативных знаний. Система предлагает традиционные модели вывода: «от фактов к цели» и «от цели к фактам». Первые версии ART опирались на язык ЛИСП, последние – на язык С.

Главное отличие между формами представления знаний KEE и ART заключается в способе, которым эти интегрированные системы связывают фреймы и правила. KEE является средой, в основе которой лежат фреймы, тогда как пакет ART основан на правилах. Описание объектов и правил в KEE представляется в виде иерархии фреймов.

Инструментальная среда J2 является развитием ЭС реального времени PICON и самой мощной системой реального времени. Работает под управлением Windows NT, возможна работа с системой в режиме «клиент – сервер» в сети Интернет. Основные функциональные воз-можности J2 связаны с поддержкой процессов слежения за множеством (порядка тысячи) одновременно изменяющихся параметров и обработкой изменений в режиме реального времени, а также с проверкой нештатных ситуаций на управляемых объектах и принятием решений как в режиме ассистирования оператору, так и в автоматическом режиме. J2 является одной из первых инструментальных сред, поддерживающих разработку интегрированных ИИ-систем.

---

Системы Work Bench в контексте автоматизации программиро-вания – это интегрированные инструментальные системы, поддерживаю-щие весь цикл создания и сопровождения программ. К основным ха-рактеристикам Work Bench-систем относятся:

использование определенной технологии проектирования на про-тяжении всего жизненного цикла (ЖЦ) системы;

вертикальная интеграция инструментальных средств, обеспечи-вающая связи и совместимость по данным между различными ин-струментами, используемыми на разных стадиях создания системы;

горизонтальная интеграция модулей и методов, используемых на одной и той же стадии проектирования;

сбалансированность инструментария, т.е. отсутствие дублирующих компонентов, необходимость и достаточность каждого инструмента.

К Work Bench-системам относятся VITAL, KEATS, SHELLY.

Глава 6. Нейронные сети
6.1. Искусственный нейрон и функции активации
Биологический нейрон содержит сому (тело нейрона), совокупность отростков – дендритов, по которым в нейрон поступают входные сигналы, и отросток – аксон, передающий выходной сигнал нейрона другим нейронам. Точка соединения дендрита и аксона называется синапсом. Общее число нейронов в головном мозгу человека превышает 100 мил-лиардов, при этом один нейрон соединен более чем с 10 тысячами соседних нейронов. Время срабатывания нейрона составляет около одной миллисекунды; чуть меньше затрачивается на передачу сигнала между двумя нейронами. Таким образом, биологический нейрон – чрезвычайно медленный процессорный элемент, уступающий быстродействию совре-менных компьютеров в миллионы раз. Тем не менее в целом мозг способен за доли секунды решать задачи, которые не в состоянии решить даже суперкомпьютер (например, узнать лицо человека, показанное в непри-вычном ракурсе).

Искусственным нейроном называется простой элемент в виде, представленном на рис. 6.1 [16, 18].

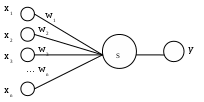
Рис. 6.1. Искусственный нейрон: 
вектор входных переменных (дендритов);

---


вектор синаптических весов; S – сома; y – выход (аксон)
Сначала вычисляется взвешенная сумма V входных переменных (скалярное произведение):



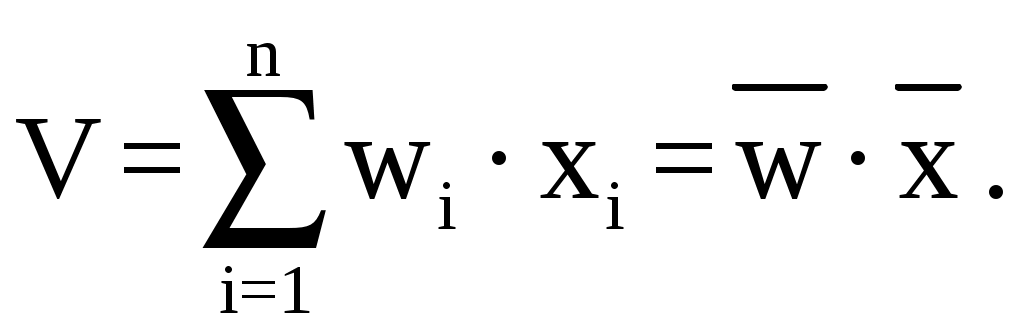
Затем полученная сумма (потенциал нейрона) сравнивается с за-данной пороговой величиной W₀. Если V W₀, то нейрон «не срабатывает», в противном случае вычисляется функция активации (решающая функ-ция) f. При этом

.

Величину порогового барьера можно рассматривать как еще один весовой коэффициент при постоянном входном сигнале.

Функции активации могут быть различных видов (линейная, ступенчатая, линейная с насыщением, многопороговая). Наиболее распространенной является сигмоидная функция с выходными значениями в интервале [0, 1]:



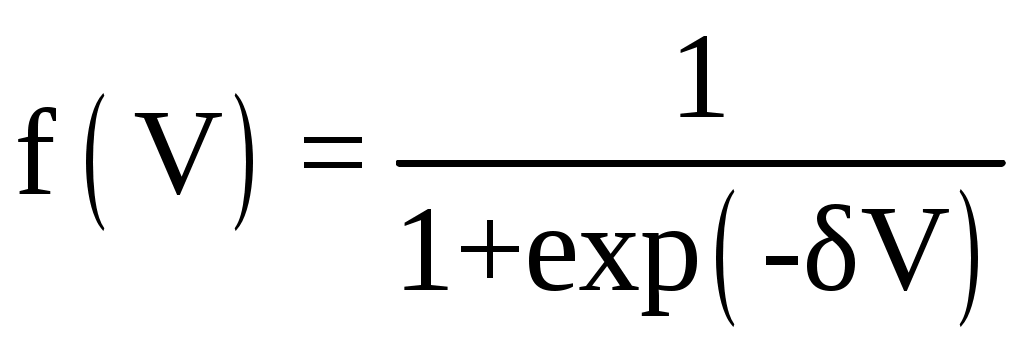
или в интервале [–1, 1]:

.

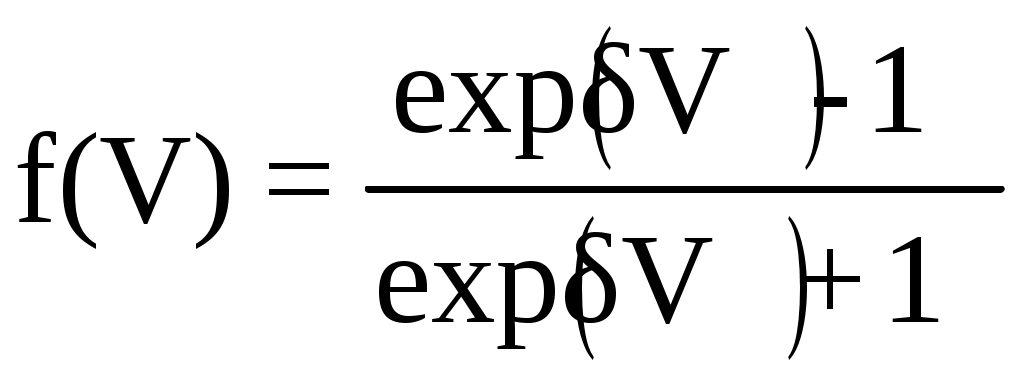Коэффициент определяет крутизну сигмоида. Поскольку сиг-моидная функция является гладким отображением , кру-тизну можно учесть через величины весов и порогов и без ограничения общности можно полагать = 1. Для учета особенностей конкретной задачи могут быть выбраны различные другие функции активации – гауссова, синусоидальная, всплеска и т.д.
6.2. Нейронные сети с прямой связью
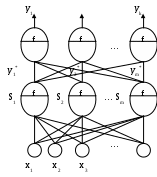
Нейронная сеть представляет собой совокупность большого числа нейронов, топология соединения которых зависит от типа сети. Нейронные сети с прямой связью состоят из статических нейронов, так что сигнал на выходе появляется в тот же момент, когда подаются сигналы на вход. Наиболее общий тип архитектуры сети получается в случае, когда все нейроны связаны друг с другом, но без обратных связей (рис. 6.2).

---

x_n

Выходные переменные

Нейроны выходного слоя

y₂

Нейроны скрытого слоя

Входные переменные

Рис. 6.2. Нейронная сеть с прямой связью

и одним скрытым слоем
Каждому нейрону соответствует свой вектор синаптических весов , множество которых образуют синаптическую матрицу . Связь с нейронами выходного слоя определяет синаптическая матрица , где m и k – число нейронов скрытого и выходного слоев соответственно.

Число нейронов скрытого слоя неограниченно возрастает при увеличении точности решения задачи. На практике рекомендуется выбирать m = (n + k)/2.

Согласно теоретическим результатам, нейронные сети с прямой связью и с сигмоидными функциями активации являются универсальным средством для аппроксимации различных функций. Любую многослойную сеть можно без потери информации трансформировать в однослойную путем пересчета синаптических матриц.

Применение нейронных сетей целесообразно для решения задач моделирования, прогнозирования, распознавания образов, если:

отсутствует алгоритм или неизвестны принципы решения задач, но накоплено достаточно большое количество примеров;

задача характеризуется большим объемом входной информации;

входные данные неполны, зашумлены и противоречивы.

Характер разработок в области нейронных сетей принципиально отличается от ЭС: последние построены на правилах типа «если…, то…», которые вырабатываются на основе формально-логических структур. В основе нейронных сетей лежит преимущественно поведенческий подход к решаемой задаче: сеть «учится на примерах» и подстраивает свои параметры при помощи алгоритмов обучения через механизм обратной связи.
Пример 6.1. Пусть n = 2, m = 2, k = 2. Порог возбуждения отсутствует, . Задана структура сети (рис. 6.3).

---