ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 88
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Для проверки данного предположения проводились полигонные испытания плети, сваренной из труб Ду 1400 мм, δ = 16,5 мм, стали Х70, после 31 года эксплуатации. Плеть содержала две области трещин глубиной 13 ÷ 60% от толщины стенки (рис. 5).
Рисунок 5. Общий вид трубной плети
Программа испытаний заключалась в циклическом нагружении плети внутренним давлением воды с параметрами Рmax = 7,4 МПа, Рmin = 5,4 МПа, в течение 3000 циклов, со сбросом давления до 0 каждые 500 циклов для приборного наблюдения за дефектами.
В результате, за 20 циклов до окончания базы испытаний было зафиксировано сквозное прорастание одной из трещин в области №1.
Измерения длин трещин показали, что большинство из них существенно подросли (до +72%). Причем максимальное приращение получили наиболее короткие сомкнутые трещины.
Изучение изломов подтвердило тенденцию, определенную в процессе испытаний - рост дефектов в глубину составил 25 ÷ 69%.
З
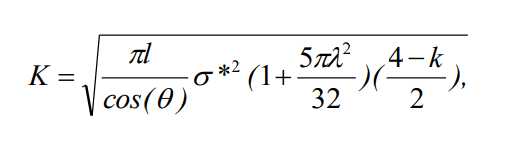афиксированные данные по развитию трещин различной глубины позволили построить кинетическую диаграмму усталостного разрушения (КДУР) плети, для которой коэффициент интенсивности напряжений (КИН)К вычислялся согласно выражению (4)
где θ = πσ*/2σс; 2 (l2 / R) 12(12 );k = (3-4μ); σ*, σс – соответственно текущее и разрушающее кольцевое напряжение в трубе без трещины, МПа; l – глубина трещины, мм; R – внешний радиус трубы, мм; δ – толщина стенки трубы, мм; μ – коэффициент Пуассона.
Полученные из КДУР количественные характеристики использовались для оценки динамики роста трещины начальной глубиной 2 мм в трубе Ду 1400 мм, δ = 15,7 мм от воздействия нестационарного нагружения, связанного с режимом транспорта газа. Для этой цели производилась обработка данных об эксплуатации 10 участков газопроводов ООО «Газпром трансгаз Югорск» с использованием программного продукта АУН-1, рассмотренного в 5 главе. В результате было установлено, что оцениваемая трещина приведет к авариям на рассматриваемых участках через 130-180 лет. Принимая во внимание, что указанные цифры получены без учета воздействия высокочастотных пульсаций и колебаний, коррозионной среды и дополнительных эксплуатационных факторов, которые в совокупности могут в десятки раз ускорять процесс развития трещин, проведенные исследования позволили заключить о необходимости анализа влияния нестационарного нагружения газопроводов при выполнении функционального диагностирования.
Энергетический фактор косвенно учитывается при проектировании газопроводов посредством коэффициента надежности по назначению. Несмотря на это, в зависимости от проектной нагрузки и типоразмера, уровень запасенной в металле труб энергии упругой деформации может существенно отличаться, что делает актуальным исследования вклада данного фактора в формирование реальных показателей сопротивляемости газопроводов разрушению.
Выполненный анализ показал, что применительно к поставленной задаче следует рассматривать энергию упругой деформации не всей конструкции, а сечения, в котором при нарушении динамического равновесия в системе (при пластической деформации, развитии микро- и макродефектов, и т. д.) происходит наибольшее ее перераспределение, и использовать в таком случае термин «удельная энергия упругой деформации».
Экспериментальные исследования проводились в два этапа.
На первом этапе из труб стали Х70, Ду 1400 мм, δ = 16,5 мм, после 31 года эксплуатации были изготовлены образцы двух типов: согласно конструкции, представленной на рисунке 4, и вырезаемые вдоль оси трубы. Количество и размеры образцов приведены в таблице 2.
Таблица 2 - Параметры изготовленных образцов из трубы стали Х70
| № группы | Тип образцов | Кол-во, шт. | Размеры рабочей части образцов | ||
| Ширина, мм | Толщина, мм | Длина, мм | |||
| I | Образцы с кольцевыми сегментами | 3 | 90 | 16,5* | 205** |
| II | Продольные образцы | 3 | 100 | 16,5 | 170 |
| III | 3 | 100 | 16,5 | 410 | |
| IV | 3 | 100 | 16,5 | 820 | |
* Толщина каждого сегмента.
** Длина рабочей части каждого сегмента.
Выбор различных конструкций обусловлен тем, что образцы с кольцевыми сегментами наиболее полно моделируют условия нагружения трубопровода, однако конструктивные особенности не позволяют существенно менять длину их рабочей части для изменения уровня запасенной энергии упругой деформации. Поэтому, сопоставляя результаты испытания образцов I и III группы, имевших одинаковый запас удельной энергии упругой деформации, можно было определить какое влияние на трещиностойкость продольных образцов оказывает несоответствие реализованных в них условий нагружения, в сравнении с нагружением трубопровода, и скорректировать результаты испытаний.
В центре рабочей части образцов наносились поперечные поверхностные трещиноподобные концентраторы напряжений.
Программа испытания заключалась в циклическом нагружении образцов до разрушения с параметрами σmax = 315 МПа, σmin = 231 МПа. Для построения КДУР применялся метод «меток».
Следующим объектом исследований была выбрана плеть, сваренная из тех же труб, из которых вырезались образцы.
На подготовленную плеть, как и в предыдущем случае, наносились трещиноподобные концентраторы напряжений. Поскольку в трубах наблюдается существенный разброс остаточных напряжений и деформаций, для получения усредненного значения трещиностойкости концентраторы наносились в различных зонах (рис. 6).
Нагружение плети внутренним давлением производилось в течение 15 000 циклов с параметрами, эквивалентными выбранным при испытании образцов:
Рmax/Pmin=7,4/5,4 МПа (σmax/σmin=315/231 МПа). Для слежения за динамикой и топографией развития трещин также применялся метод «меток».
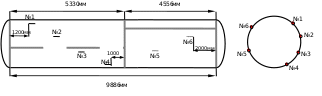
Рисунок 6 - Схема расположения концентраторов в трубной плети
Используя положения механики деформирования твердых тел были выведены соотношения для определения удельной энергии упругой деформации Wуд испытываемых конструкций:
для образцов I группы:
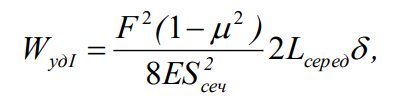(5)для образцов II – IV группы:
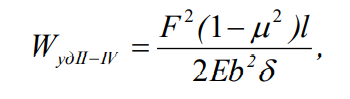(6)для трубной плети:
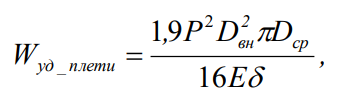(7)где F – сила, действующая на образец, Н; Sсеч - площадь поперечного сечения сегмента трубы в образце, м2; Lсеред- длина дуги сегмента трубы по его срединной линии, м; Dвн, Dср – соответственно внутренний и средний диаметр труб, м; l, b – соответственно длина и ширина образца, м.
Обработка экспериментальных данных и вычисление согласно соотношениям (5) – (7) соответствующих значений Wуд при выбранных параметрах нагружения позволили установить влияние энергетического фактора на циклическую трещиностойкость испытанных конструкций (рис. 7).
Путем представления результатов через относительное снижение трещиностойкости получено эмпирическое выражение для определения коэффициента KW, учитывающего влияние удельной энергии упругой деформации на сопротивляемость трубопровода циклическому разрушению:
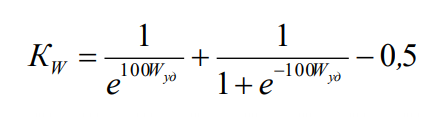(8)
Рисунок 7 - Зависимость трещиностойкости образцов II – IV группы и трубной плети от запасенной в них удельной энергии упругой деформации
Корректность эмпирического выражения (8) оценивалась достоверностью аппроксимации им экспериментальных данных, согласно уравнению:
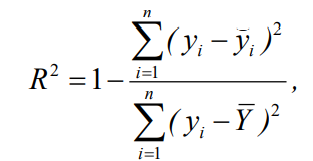(9) где R2– коэффициент достоверности аппроксимации; yi – экспериментальные значения; ўi – значения функции регрессии; Ῡ - среднее арифметическое экспериментальных значений; n – количество экспериментальных значений.
Выполненная обработка дала результат R2 = 0,8839.
Применимость полученной зависимости для других трубных сталей и при других эксплуатационных нагрузках исследовалась на втором этапе. Изтрубы стали 17Г1С, Ду 1200 мм, δ = 12,4 мм, находящейся в аварийном запасе, вырезалось три группы продольных образцов (табл. 3).
Таблица 3 - Параметры образцов, вырезанных из трубы стали 17Г1С
| № группы | Количество, шт. | Ширина рабочей части, мм | Толщина, мм | Длина рабочей части, мм |
| I | 3 | 100 | 12,4 | 170 |
| II | 3 | 100 | 12,4 | 410 |
| III | 3 | 100 | 12,4 | 820 |
В центральной части образцов, также как и в предыдущем случае, наносились трещиноподобные концентраторы.
Программа испытаний заключалась в циклическом нагружении образцов до разрушения при σmax
= 260 МПа, σmin = 100 МПа.
Обработка результатов сводилась к определению значений Wуд при выбранных параметрах нагружения и представлению данных через относительное снижение трещиностойкости.
Вычисление согласно уравнению (9) достоверности аппроксимации выражением (8) полученного на втором этапе корреляционного поля дало
R2 = 0,6953.
Таким образом, проведенные исследования показали, что влияние удельной энергии упругой деформации газопровода на его сопротивляемость разрушению является значительным, носит системный характер и может быть с достаточной степенью точности отражено полученным эмпирическим выражением.
Также следует особо отметить, что выражение (8) не является универсальным и применимо только к трубным конструкциям, изготовленным из анализированных классов сталей, нагружаемым в исследованном диапазоне значений внутреннего давления (5,4 ÷ 7,4 МПа). В остальных случаях корректность его использования нуждается в дополнительном экспериментальном подтверждении.