Файл: Методические указания к лабораторной работе по курсу Технологии анализа данных для студентов, обучающихся по основной образовательной программе.docx

Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Комсомольский-на-Амуре государственный университет» Кафедра "Информационные системы"

ПАРНАЯ КОРРЕЛЯЦИЯ Методические указания к лабораторной работе по курсу «Технологии анализа данных» для студентов, обучающихся по основной образовательной программе бакалавров по направлениям 09.03.03 «Прикладная информатика»

Комсомольск-на-Амуре 2019

Введение

Парная регрессия характеризует связь между двумя признаками: результативным и факторным. Во многих случаях форма линии регрессии устанавливается путем выбора из заданного множества стандартных зависимостей, к числу которых, прежде всего, относятся:

• 
  линейная зависимость                   ;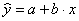
  
• 
  степенная зависимость                  ;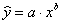
  
• 
  показательная зависимость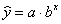          
  
• 
  гиперболическая зависимость      ;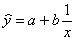
  
• 
  логарифмическая зависимость     ;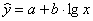
  
• 
  полиномиальная зависимость      ,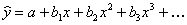
  

где    - неизвестные параметры линии регрессии;

           -  уравнение регрессии.

---

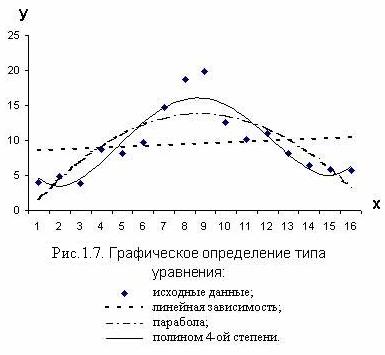
Определить тип уравнения можно, исследуя зависимость графически. Предположим, у нас есть некоторые статистические данные, для которых мы хотим подобрать линию регрессии (рис. 1.7). На рисунке показаны три такие «пробы». Нетрудно видеть, что полиномиальная зависимость «лучше» линейной. А из двух полиномов (2-ой и 4-ой степени)  «лучшим» является полином 4-ой степени.



Однако существуют более общие указания, позволяющие выявить уравнение связи, не прибегая к графическому изображению. Если результативный и факторный признаки возрастают одинаково, примерно в арифметической прогрессии, то это свидетельствует о том, что связь между ними линейная, а при обратной связи – гиперболическая. Если факторный признак увеличивается в арифметической прогрессии, а результативный – значительно быстрее, то используется параболическая или степенная регрессия.

1 Задание

Известны данные по регионам России за 2019 год о среднемесячной номинальной начисленной заработной плате работников и прожиточном минимуме, рублей.

1) Постройте поле корреляции и сформулируйте гипотезу о форме связи.

2) Рассчитайте параметры уравнений парных регрессий:

- линейной;

- степенной;

- логарифмической;

- показательной.

3) Для каждой из регрессий:

- вычислите средние ошибки аппроксимации, сделайте выводы о качестве эконометрических моделей;

- совместите на одном графике поле корреляции и линию регрессии;

- оцените тесноту связи с помощью показателей корреляции и детерминации;

- оцените с помощью F-критерия Фишера статистическую надёжность результатов регрессионного моделирования;

- выберите лучшее уравнение регрессии и дайте его обоснование.

4) Сделайте выводы.

Исходные данные приведены в таблицах ниже.

Таблица 1 – Номера регионов из таблицы 2 (по вариантам)

Варианты
1	2	3	4	5	6	7	8	9	10	11	12	13	14
1	2	3	4	5	6	7	1	2	3	4	5	6	7
6	7	8	9	10	10	12	7	8	9	10	11	12	13
11	12	13	14	15	14	17	13	14	15	16	17	18	19
16	17	18	19	20	18	22	19	20	21	22	23	24	25
21	22	23	24	25	22	27	25	26	27	28	29	30	31
26	27	28	29	30	26	32	31	32	33	34	35	36	37
31	32	33	34	35	30	37	37	38	39	40	41	42	43
36	37	38	39	40	34	42	43	44	45	46	47	48	48
41	42	43	44	45	41	49	49	50	51	52	53	54	53
46	47	48	49	50	48	56	55	55	57	58	59	60	58
51	52	53	54	55	55	63	61	60	63	64	65	65	63
56	57	58	59	60	62	70	67	65	69	70	71	70	68
61	62	63	64	65	69	77	73	70	75	76	77	75	73
71	67	68	74	70	76	84	79	75	81	82	82	80	78
84	72	73	83	75	83	85	85	80	84	85	84	85	83

---

Таблица 2 – Данные о среднемесячной номинальной начисленной заработной плате работников и прожиточном минимуме по регионам РФ в 2019 году, тыс. рублей

Номер региона	Наименование региона	Начисленная заработная плата	Прожиточный минимум на душу населения
1	Алтайский край	27,962	9,490
2	Амурская область	47,234	10,980
3	Архангельская область	49,435	12,090
4	Астраханская область	36,093	9,622
5	Белгородская область	34,615	9,467
6	Брянская область	29,853	9,880
7	Владимирская область	33,076	10,872
8	Волгоградская область	33,371	9,318
9	Вологодская область	39,116	10,382
10	Воронежская область	33,690	8,966
11	Еврейская авт.область	42,400	12,825
12	Забайкальский край	43,896	11,290
13	Ивановская область	27,553	10,102
14	Иркутская область	46,387	11,235
15	Кабардино-Балкарская Республика	27,466	9,800
16	Калининградская область	35,637	10,980
17	Калужская область	41,442	10,482
18	Камчатский край	80,448	19,555
19	Карачаево-Черкесская Республика	26,955	9,335
20	Кемеровская область	41,770	9,476
21	Кировская область	30,213	9,675
22	Костромская область	31,421	11,914
23	Краснодарский край	36,133	10,900
24	Красноярский край	49,932	10,238
25	Курганская область	30,632	10,349
26	Курская область	32,709	9,280
27	Ленинградская область	46,387	10,450
28	Липецкая область	34,312	8,734
29	Магаданская область	94,856	18,146
30	Москва	94,294	16,463
31	Московская область	55,555	12,229
32	Мурманская область	63,715	14,890
33	Ненецкий авт.округ	88,027	20,460
34	Нижегородская область	35,212	10,900
35	Новгородская область	32,174	10,652
36	Новосибирская область	39,076	10,843
37	Омская область	35,368	9,250
38	Оренбургская область	32,883	8,816
39	Орловская область	29,683	10,897
40	Пензенская область	30,765	9,783
41	Пермский край	39,210	10,098
42	Приморский край	46,867	12,537
43	Псковская область	29,441	10,651
44	Республика Адыгея	30,192	9,232
45	Республика Алтай	33,387	10,560
46	Республика Башкортостан	36,465	9,014
47	Республика Бурятия	39,115	10,823
48	Республика Дагестан	26,835	9,301
49	Республика Ингушетия	27,410	9,678
50	Республика Калмыкия	28,617	9,000
51	Республика Карелия	42,964	13,030
52	Республика Коми	53,416	12,948
53	Республика Крым	32,748	10,900
54	Республика Марий Эл	30,152	9,780
55	Республика Мордовия	28,826	9,340
56	Республика Саха (Якутия)	73,402	16,463
57	Республика Северная Осетия - Алания	28,751	9,767
58	Республика Татарстан	37,418	9,349
59	Республика Тыва	39,673	10,102
60	Республика Хакасия	40,548	10,897
61	Ростовская область	33,757	9,671
62	Рязанская область	34,488	9,821
63	Самарская область	36,431	10,900
64	Санкт-Петербург	65,872	11,007
65	Саратовская область	30,717	9,637
66	Сахалинская область	87,418	15,786
67	Свердловская область	41,110	11,345
68	Севастополь	34,621	10,980
69	Смоленская область	31,269	10,364
70	Ставропольский край	31,836	9,089
71	Тамбовская область	28,697	8,861
72	Тверская область	33,524	10,410
73	Томская область	45,526	11,179
74	Тульская область	38,151	9,915
75	Тюменская область	48,613	10,887
76	Удмуртская Республика	34,052	9,150
77	Ульяновская область	30,677	9,682
78	Хабаровский край	50,213	15,089
79	Ханты-Мансийский авт.округ - Югра	75,087	14,512
80	Челябинская область	37,433	9,592
81	Чеченская Республика	27,757	9,664
82	Чувашская Республика	29,671	9,560
83	Чукотский авт.округ	107,107	21,441
84	Ямало-Ненецкий авт.округ	101,012	20,670
85	Ярославская область	36,016	9,695

---

---

2 Основные теоретические сведения

Графически взаимосвязь двух признаков изображается с помощью поля корреляции. В системе координат по оси абсцисс откладываются значения факторного признака, а по оси ординат – результативного. Каждое пересечение линий обозначается точкой. При отсутствии связи имеет место беспорядочное расположение точек на графике. Чем сильнее связь между признаками, тем теснее будут группироваться точки вокруг определённой линии, выражающей форму связи (рис. 2).



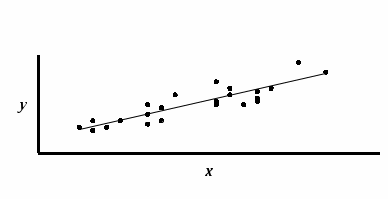
Рисунок 2 - График корреляционного поля

Приведённый на рис.2 график показывает, что с увеличением величины х значение у в среднем также возрастает.

2.1 Регрессии

Линейная зависимость

Линейная регрессия сводится к нахождению уравнения вида



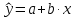
Для определения значений неизвестных параметров а и b при линейной зависимости в общем случае применяют метод наименьших квадратов (МНК), с помощью которого получают уравнения для нахождения искомых параметров а и b:

;

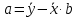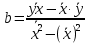
где

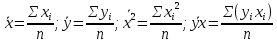
n - объем исследуемой совокупности (число единиц наблюдений).
Пример 1. Пусть имеются данные (см. табл. 3), характеризующие деловую активность акционерных обществ закрытого типа: прибыль (тыс. р.) и затраты на 1 р. произведенной продукции (коп.).

Требуется найти уравнение регрессии для данного примера.

Таблица 3 – Исходные данные

номер п/п	Затраты на 1 руб. продукции, коп.	Прибыль, тыс.р.
	хi	уi
1	77	1070
2	77	1001
3	81	789
4	82	779
5	89	606
6	96	221
Сумма	502	4466
Среднее	83,66	744,33

---