Файл: Методические указания к лабораторной работе по курсу Технологии анализа данных для студентов, обучающихся по основной образовательной программе.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 49
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Решение. В соответствии с условием задачи прибыль будет результативным признаком (у), а затраты на 1 р. произведенной продукции будут факторным признаком или просто фактором (х).
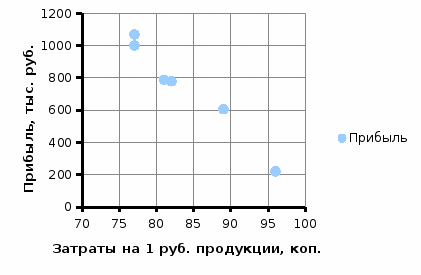
Рисунок 1 – График корреляционного поля по данным таблицы 3
Корреляционное поле, построенное по данным табл. 3 (см. рис. 1), позволяет предположить наличие линейной зависимости между рассматриваемыми признаками.

Система нормальных уравнений для данного примера имеет вид
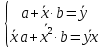
Искомые параметры а и b
 ;
; 
где

Рассчитаем средние величины, для удобства расчёты сведём в таблицу 4. В последней строке таблицы расположены данные о значении средних величин:
Таблица 4– Расчётная таблица
| номер п/п | Затраты на 1 руб. продукции, коп. | Прибыль, тыс.р. | Расчётные данные | ||
| хi | уi | x2 | y∙x | 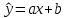 | |
| 1 | 77 | 1070 | 5929 | 82390 | 1012,86 |
| 2 | 77 | 1001 | 5929 | 77077 | 1012,86 |
| 3 | 81 | 789 | 6561 | 63909 | 851,74 |
| 4 | 82 | 779 | 6724 | 63878 | 811,46 |
| 5 | 89 | 606 | 7921 | 53934 | 529,51 |
| 6 | 96 | 221 | 9216 | 21216 | 247,55 |
| Сумма | 502 | 4466 | 42280 | 362404 | 4466 |
| Среднее | 83,66 | 744,33 | 7046,67 | 60400,67 | 744,33 |
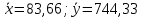
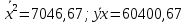
Сначала вычислим значение коэффициента регрессии b:

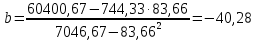
Далее находим параметр a :
 ;
; 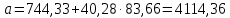
Следовательно, линейное уравнение регрессии будет выглядеть следующим образом:
 ,
,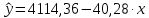
Подставляя в это уравнение табличные значения х, вычислим табличные значения
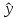 .
.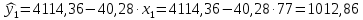
и так далее. Результаты приведены в последней колонке таблицы 4.
Дополним поле корреляции линией регрессии (рис. 2).
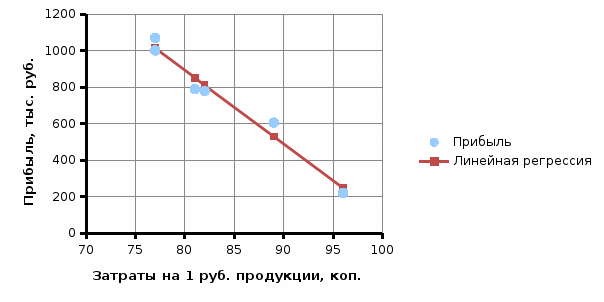
Рисунок 2 – Линейная регрессия по данным таблицы 4
Параметры нелинейных регрессий (степенной, показательной и т.д.) также находятся с помощью метода наименьших квадратов. Только необходимо сначала линеаризировать их, т.е. привести к линейному виду.
Степенная зависимость. Уравнение нелинейной степенной регрессии -
Пусть
Применив МНК, находим
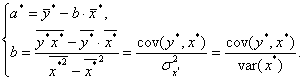 Значение параметра а находим в результате потенцирования а*: 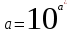
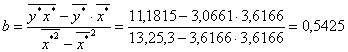 , ,Значение параметра а находим в результате потенцирования а*: Таким образом, уравнение степенной регрессии будет иметь следующий вид: Расчетные значения представлены в последнем столбце табл. 1.5. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Показательная зависимость. Уравнение нелинейной показательной регрессии - Логарифмическая зависимость. Уравнение нелинейной логарифмической регрессии - где В результате применения МНК получим 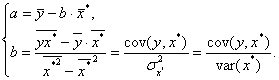 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Гиперболическая зависимость. Уравнение нелинейной гиперболической регрессии -
2.2 Показатели корреляции
При анализе можно рассчитывать среднюю ошибку аппроксимации – среднее отклонение расчетных значений от фактических:
Ее значение должно быть в интервале от 8 до 10 %. Если значение средней ошибки аппроксимации больше, то отклонение сильно большое, и использовать модель нецелесообразно.
Перейдем к оценке тесноты корреляционной зависимости. Рассмотрим наиболее важный для практики и теории случай линейной зависимости вида:
Коэффициент, использующий средние квадратические отклонения факторов называется коэффициентом корреляции и выражается формулой
Коэффициент корреляции характеризует тесноту или силу связи между переменными х и у.
При
Свойства коэффициента корреляции:
коэффициент линейной корреляции изменяется в пределах от - 1 до + 1;
- связь слабая;
| , |
Следует иметь в виду, что величина линейного коэффициента корреляции оценивает тесноту связи рассматриваемых признаков в ее линейной форме.
Для нелинейных регрессий определяют не коэффициент корреляции, а индекс корреляции:
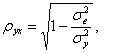
где
2.3. Коэффициент детерминации
Одной из наиболее эффективных оценок адекватности регрессионной модели, мерой качества уравнения регрессии, (или, как говорят, мерой качества подгонки регрессионной модели к наблюденным значениям
Коэффициент детерминации – квадрат коэффициента или индекса корреляции.
Величина