Файл: Методические указания к лабораторной работе по курсу Технологии анализа данных для студентов, обучающихся по основной образовательной программе.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 43
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
.
.
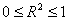Чем ближе
к единице, тем лучше регрессия аппроксимирует эмпирические данные, тем теснее наблюдения примыкают к линии регрессии. Если 
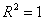, то эмпирические (фактические) точки (
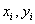) лежат на линии регрессии и между переменным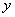и 
и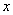 
существует линейная функциональная зависимость. Если 
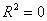, то вариация зависимой переменной полностью обусловлена воздействием неучтенных в модели переменных, и линия регрессии параллельна оси абсцисс.
Поскольку величина коэффициента детерминации служит одним из критериев оценки качества модели, то, разумеется, при подборе уравнения регрессии для каких-то фактических данных, из всей совокупности регрессий выбирается та, которая в состоянии объяснить большую долю вариации зависимой переменной по сравнению с другими регрессионными уравнениями.
Проверка значимости уравнения регрессии производится на основе дисперсионного анализа.
Проверить значимость уравнения регрессии – значит, установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих факторов (одного или нескольких) для описания результативного фактора.
После того как найдено уравнение регрессии, производится оценка значимости как уравнения в целом, так и отдельных его параметров.
Оценка значимости уравнения регрессии в целом дается с помощью F-критерия Фишера-Снедекора (так называемый F- тест). При этом выдвигается нулевая гипотеза, что коэффициент регрессии равен нулю, т.е. b=0 и, следовательно, фактор x не оказывает влияния на результат y.
Непосредственному расчету
F-критерия предшествует анализ дисперсии. Центральное место в нем занимает разложение общей суммы квадратов отклонений переменной у от среднего значения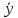
на две части – «объясненную» и «необъясненную».
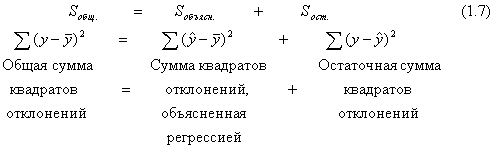
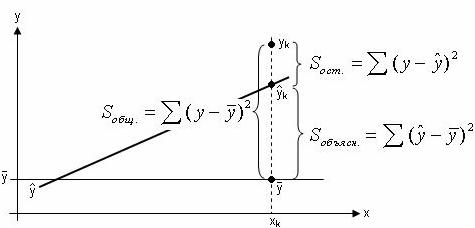
Рис. 2 - Соотношение общей вариации признака, его
составляющей, объясняемой влиянием фактора
, и остаточной вариации
Поскольку не все точки поля корреляции лежат на линии регрессии, то всегда имеет место их разброс как обусловленный влиянием фактора , т.е. регрессией 
по , так и вызванный действием прочих причин (необъясненная вариация). Пригодность линии регрессии для прогноза зависит от того, какая часть общей вариации признака приходится на объясненную вариацию. Очевидно, что если сумма квадратов отклонений, обусловленная регрессией, будет больше остаточной суммы квадратов, то уравнение регрессии статистически значимо и фактор оказывает существенное воздействие на результат . Это равносильно тому, что коэффициент детерминации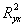 
будет приближаться к единице.
Английским статистиком Снедекором разработаны таблицы критических значений F-отношений при разных уровнях существенности нулевой гипотезы и различном числе степеней свободы.
Оценивание каждого параметра в уравнении регрессии поглощает одну степень свободы в выборке. Отсюда число степеней свободы равняется количеству наблюдений в выборке минус количество оцениваемых параметров. Параметрами являются постоянный член и коэффициенты при независимых переменных (в парной регрессии независимая переменная одна - х). В рассматриваемом случае парной регрессии оцениваются только два параметра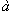
и 
, поэтому число степеней свободы составляет 
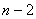, где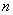 
- количество измерений в выборке.
Табличное значение F-критерия (Fтабл )- это максимальная величина отношения дисперсий, которая может иметь место при случайном их расхождении для данного уровня вероятности наличия нулевой гипотезы. Другими словами, Fтабл. – это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости α . Уровень значимости α – это вероятность отвергнуть правильную гипотезу при условии, что она верна. Обычно α принимается равной 0,05 или 0,01, т.е. 5% или 1% уровень значимости.
Вычисленное значение F-отношения Fфакт признается достоверным (отличным от единицы), если оно больше табличногоFтабл. В этом случае нулевая гипотеза об отсутствии связи признаков отклоняется и делается вывод о существенности этой связи: Fфакт > Fтабл .
Если же величина окажется меньше табличной Fфакт < Fтабл, то вероятность нулевой гипотезы выше заданного уровня (например, 0,05 (5%)) и она не может быть отклонена без серьезного риска сделать неправильный вывод о наличии связи. В этом случае уравнение регрессии считается статистически незначимым.
Величина F-критерия связана с коэффициентом детерминации
R2yx и для парной регрессии его значение можно выразить так:
,
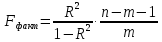где m – число параметров при переменных х (для линейной и приводимым к линейной регрессиям m=1),
n – число наблюдений.
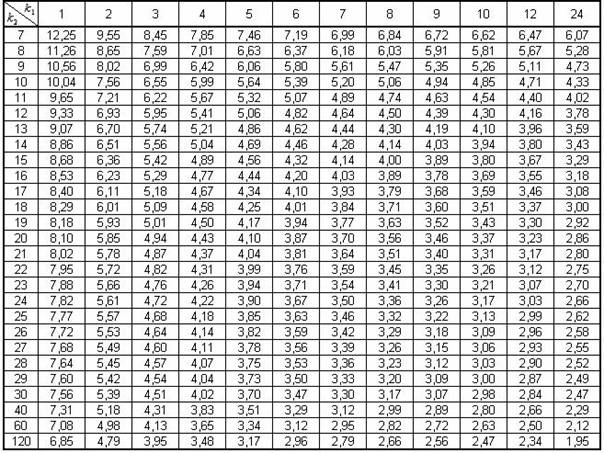
СТАТИСТИКО-МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
Таблица значений F-критерия Фишера при уровне значимости в 5%
(α = 0,05)
Здесь k1 = m, k2 = n – m – 1,
где m – число параметров при переменных х (для линейной, степенной, логарифмической, показательной, гиперболической регрессий m=1),
n – число наблюдений.
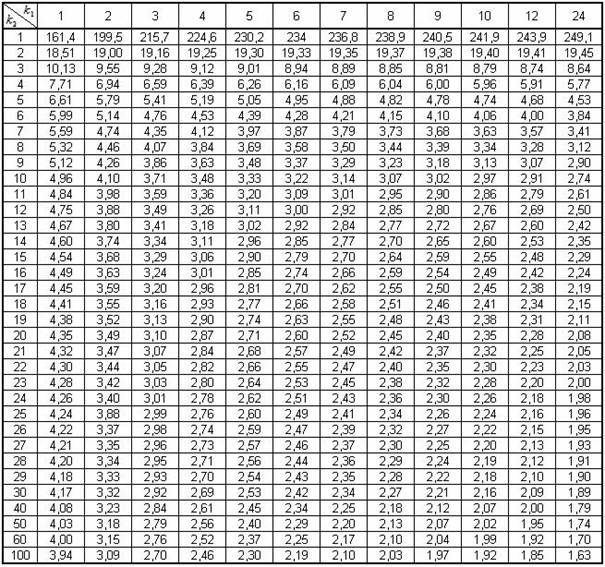
Таблица П.2
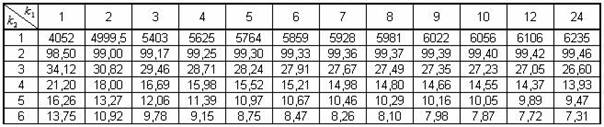
Таблица значений F-критерия Фишера при уровне значимости в 1%
(α = 0,01)
.Чем ближе
к единице, тем лучше регрессия аппроксимирует эмпирические данные, тем теснее наблюдения примыкают к линии регрессии. Если , то эмпирические (фактические) точки ( ) лежат на линии регрессии и между переменными и существует линейная функциональная зависимость. Если , то вариация зависимой переменной полностью обусловлена воздействием неучтенных в модели переменных, и линия регрессии параллельна оси абсцисс.Поскольку величина коэффициента детерминации служит одним из критериев оценки качества модели, то, разумеется, при подборе уравнения регрессии для каких-то фактических данных, из всей совокупности регрессий выбирается та, которая в состоянии объяснить большую долю вариации зависимой переменной по сравнению с другими регрессионными уравнениями.
2.4. Оценка значимости уравнения регрессии
Проверка значимости уравнения регрессии производится на основе дисперсионного анализа.
Проверить значимость уравнения регрессии – значит, установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих факторов (одного или нескольких) для описания результативного фактора.
После того как найдено уравнение регрессии, производится оценка значимости как уравнения в целом, так и отдельных его параметров.
Оценка значимости уравнения регрессии в целом дается с помощью F-критерия Фишера-Снедекора (так называемый F- тест). При этом выдвигается нулевая гипотеза, что коэффициент регрессии равен нулю, т.е. b=0 и, следовательно, фактор x не оказывает влияния на результат y.
Непосредственному расчету
F-критерия предшествует анализ дисперсии. Центральное место в нем занимает разложение общей суммы квадратов отклонений переменной у от среднего значения
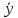на две части – «объясненную» и «необъясненную».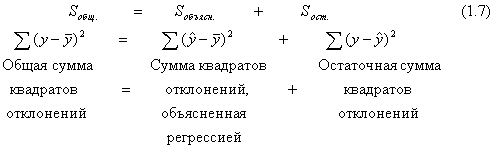 Рис. 2 - Соотношение общей вариации признака, его
составляющей, объясняемой влиянием фактора
, и остаточной вариацииПоскольку не все точки поля корреляции лежат на линии регрессии, то всегда имеет место их разброс как обусловленный влиянием фактора
, т.е. регрессией по , так и вызванный действием прочих причин (необъясненная вариация). Пригодность линии регрессии для прогноза зависит от того, какая часть общей вариации признака приходится на объясненную вариацию. Очевидно, что если сумма квадратов отклонений, обусловленная регрессией, будет больше остаточной суммы квадратов, то уравнение регрессии статистически значимо и фактор оказывает существенное воздействие на результат . Это равносильно тому, что коэффициент детерминации будет приближаться к единице.Английским статистиком Снедекором разработаны таблицы критических значений F-отношений при разных уровнях существенности нулевой гипотезы и различном числе степеней свободы.
Оценивание каждого параметра в уравнении регрессии поглощает одну степень свободы в выборке. Отсюда число степеней свободы равняется количеству наблюдений в выборке минус количество оцениваемых параметров. Параметрами являются постоянный член и коэффициенты при независимых переменных (в парной регрессии независимая переменная одна - х). В рассматриваемом случае парной регрессии оцениваются только два параметра
и , поэтому число степеней свободы составляет , где - количество измерений в выборке.Табличное значение F-критерия (Fтабл )- это максимальная величина отношения дисперсий, которая может иметь место при случайном их расхождении для данного уровня вероятности наличия нулевой гипотезы. Другими словами, Fтабл. – это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости α . Уровень значимости α – это вероятность отвергнуть правильную гипотезу при условии, что она верна. Обычно α принимается равной 0,05 или 0,01, т.е. 5% или 1% уровень значимости.
Вычисленное значение F-отношения Fфакт признается достоверным (отличным от единицы), если оно больше табличногоFтабл. В этом случае нулевая гипотеза об отсутствии связи признаков отклоняется и делается вывод о существенности этой связи: Fфакт > Fтабл .
Если же величина окажется меньше табличной Fфакт < Fтабл, то вероятность нулевой гипотезы выше заданного уровня (например, 0,05 (5%)) и она не может быть отклонена без серьезного риска сделать неправильный вывод о наличии связи. В этом случае уравнение регрессии считается статистически незначимым.
Величина F-критерия связана с коэффициентом детерминации
R2yx и для парной регрессии его значение можно выразить так:
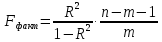,где m – число параметров при переменных х (для линейной и приводимым к линейной регрессиям m=1),
n – число наблюдений.
СТАТИСТИКО-МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
Таблица значений F-критерия Фишера при уровне значимости в 5%
(α = 0,05)
Здесь k1 = m, k2 = n – m – 1,
где m – число параметров при переменных х (для линейной, степенной, логарифмической, показательной, гиперболической регрессий m=1),
n – число наблюдений.
Таблица П.2
Таблица значений F-критерия Фишера при уровне значимости в 1%
(α = 0,01)