Тең векторлар. 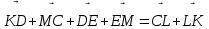теңдігі орындалады ма?

_{Сұрақ: Векторларды қосуда екі теңдік тең бе?}

Шешуі: Осыдан іздеуге бейім бала екінші вектордың басын алдыңғы вектордың ұшына келетіндей етіп шығару керектігін түсініп, вектордың қосындысындағы қосылғыштардың орындарын қалауынша ауыстырып қосуда есепті шешудің оңтайлы әдісін топтап, өзіне жеңілдетіп алар еді. Сөзімізді нақтыласақ, 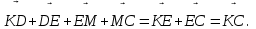Теңдіктің оң жағында .

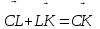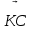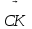Осы жерде оқушылар уәждемелік қызмет қарама-қайшылыққа тап болады олардың шешімі және векторлары өзара тең бе немесе тең емес пе? деген сұраққа әкеліп тіреледі. Бұл проблеманы шешуде оқушылардың ойлауында тең векторлар ұғымының анықтамасы еске түсірілуі қажет.

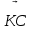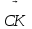Анықтама бойынша векторлар тең болуы үшін олардың ұзындықтары тең және бағыттары бірдей болуы тиіс. Осыған байланысты, оқушылар өздері мынадай қорытындыға келеді: анықтама бойынша екінші шарт орындалмағаннан кейін және векторлары өзара қарама-қарсы бағытталғандықтан оларды тең векторлар деп атай алмаймыз. Яғни, бұл есептің жауабы: бастапқы екі теңдік тең емес.

Белгісізді табу. Берілген 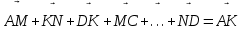теңдік орындалуы үшін қандай вектордың жетіспейтіндігін табу. Мұнда оқушының зерттеу қабілетін дамытуға арналған фундаменталды критерий бойынша, базалық бұрынғы өткен білімін қолдану аясында есептің шешімін таба алады. Олардың ойлау актілері: теңдеу секілді шешуге, теңбе-теңдікті дәлелдеу үшін талпынысқа жол ашуға, амалдар қолдануға, ізденіс белсенділігін арттыруға мүмкіндік береді.

Векторлар арқылы өрнекті құру. Өрнекті оқушылардың өзіне құруға берілген. Шарт бойынша ABCD параллелограмы берілг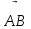ен. мен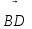

---

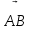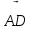векторларын және векторлары арқылы өрнектеу қажет.

Алдымен есептің шартын жақсы түсіну, одан кейін оқушылар өз-өзіне кезегімен сұрақтар қояды: «Не белгілі?, Не берілген?, Ізделіндіні анықтау үшін берілгендер жеткілікті ме?» және т.с.с. Мұғалім әрі қарай суретін сызуға кеңес береді, қысқаша шартын жазу, оны бөліктерге бөлу. Сол секілді ұқсас есепті еске түсірген немесе оның шешу әдісін пайдалану пайдалы.

Жалпы кез-келген есепті векторлардың көмегімен шешу процесінің кезеңдері бар. Олар: қолайлы түрде векторларды енгізе отырып, есептің шартын векторлар көмегімен жазу; есептің шартын түрлендіре отырып, шешуін векторлық түрде алу; алынған жауапты есептің бастапқы геометриялық мағынасына келтіріп жазу керек.

Жазықтықтағы түрлендірулер. Центрлік және осьтік симметрия.

Оқушыларға бұл ұғым таныс болғандықтан, еске түсіру мақсатында симметриялы ою-өрнектер, симметриялы сызбалар, симметриялы фигураларды қолданған жөн.

Мұғалім: Суретте не берілген және осы суреттен қандай тұжырым жасауға болады?- деу арқылы оқушыларды өзіне қаратып, бүгінгі өтілетін жаңа тақырыптың мәнін ашып, қызықтыруына болады. Олар тақтадағы суретті сипаттауға көшеді (1-сурет).


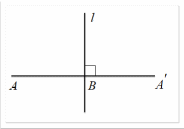
1-сурет
Оқушылардың тарапынан ұсынылуы мүмкін болған жауаптарды 2-кестеден көруімізге болады.

2-кесте.

№	Ұсынылуы мүмкін болған жауаптар	Ұсынылатын тақырыптың болжамы	Ұсынылған болжамды тексеру кезіндегі оқушының зерттеу қабілеттілік деңгейі
1	l түзуі берілген, АВ оған перпендикуляр.	Түзулердің перпендикулярлығы	Нақты объектімен жұмыс жасайды.
2	AA’ және l түзулері өзара қиылысып жатыр. Қиылысу нүктесі В деп белгіленген.	Екі түзудің қиылысуы немесе орналасуы	Бастапқы мәліметті жобалайды және болжамды ұсына алады.
3	Жазықтықта l түзуі берілген. А нүктесіне қарама-қарсы A’ бейнесі салынған және ол В нүктесі арқылы өтеді.	Жазықтықтағы түрлендірулер	«Бейне», «түпбейне» ұғымдарын біледі, өтілген тақырыпты қолдана алады.
4	А нүктесінің симметриясы A’нүктесі. Олар l түзуіне перпендикуляр.	Симметрия	Шығармашылық ойлауға дайын, алынған мәліметті болжап, жаңа міндеттерді қоя алады.
5	Координаталық жазықтыққа ұқсайды, О нүктесінің орнында В нүктесі орналасқан.	Декарттық координаталар жүйесі	Базалық білімі бар, есте сақтауы жоғары бірақ, ойлаудың сынилығы байқалмайды.
6	Жазықтықта түзуден тыс жатқан нүкте арқылы осы түзуге перпендикуляр жүргізу	Түзу және жазықтықтың орналасуы	Ойлау икемділігі орташа, стандартты есептерді шығара алады.
7	ВA’= АВ теңдігі көрініп тұр және 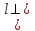AA’орналасқан.	Нүктеден түзуге дейінгі арақашықтық	Талдау жасай алады, бірақ ойын жинақтап қорытындылай алмайды.
8	А нүктесі A’ нүктесіне симметриялы көшірілген.	Параллел көшіру	Ойлау икемділігі жоғары, тақырыптардың байланысын сыни көзбен байқап жорамалдайды.

---

Берілген жауаптардан байқайтынымыз: көбінесе оқушылардың нақты объектімен жұмыс жасап, яғни стандартты есептерге үйреніп қалған баланың жауапты еш ойланбастан тез беруге ұмтылатындығы, осылайша болжамның ақиқаттығына көз жеткізгенде өз ойының кемшіл тұсы бар екендігін көреді. Әрине, өз ойын ортада көпшілік алдында жариялаудың өзі жетістік екендігі сөзсіз. Бірақ та, геометрия есептері көзге нақты көрінгенімен, интеллектуалды-логикалық ойлаудың сынилығын, яғни бір сөзбен айтқанда шығармашылық және эвристикалық ойлауды қажет етеді. Оқушылардың тақырыпты табуға оның мәнін ашуға байланысты ұсынылған болжамдарында зерттеу қызметінің кейбір кезеңдері көрініс тапты: алынған материалдарға талдау жасау; оларды өңдеу; уәждемелік қызмет; негізгі ұғымдарды анықтау т.с.с.

Сонымен қоса, центрлік және өстік симметрия тақырыбына есептер шығаруда келесі түрдегі нұсқаулықты ұсынуға болады:

1. 
   центрлік симметрияда нүктелердің арақашықтығы сақталады [16];
   
2. 
   центрлік симметрияда кері бейнелеу орындалады;
   
3. 
   өстік симметриялы фигуралар өзара тең болады;
   
4. 
   центрлік симметрия нүктеге және өстік симметрия түзуге қарағанда симметриялы бейнеленеді;
   
5. 
   өстік симметрия орын ауыстырудың бір түрі болғандықтан центрлік симметрияның барлық қасиеттері орындалады.
   

Негізінен кез-келген тапсырманы орындатуда мұғалім кейбір нұсқаулықтарды беруі міндетті. Нұсқаулық оқушыға тапсырмаларды шешу кезінде көмектеседі бірақ, оның шешімін оқушының өзі тапқаны жөн.

Оқушыларға берілетін тапсырмалардың ішінде орындалуы тез есептерді шығарту олардың ынтасын, жаңа тақырыпты игеруге деген құлшынысын жойып алмауға септігін тигізеді. Зерттеп оқыту кезінде жүргізілінетін зерттеу жұмысы бір сабақпен ғана шектелуі мүмкін. Ұзақ мерзімді талап ететін зерттеу жұмыстарының нәтижелілігі орындалу деңгейіне қарай арта түседі.

Ұсынылатын келесі тапсырмалар легі алғашқы сәттен-ақ өз жауабын тапса да, оқушылардың орындауын қадағалау маңызды.

1. А,В,О нүктелері,CD кесіндісі және l түзуі берілген.

1) Берілген нүктелерге l осіне қарағанда симметриялы нүктелерді,берілген кесіндіге симметриялы кесіндіні салыңдар;

2) О центріне қарағанда симметриялы фигураларды салыңдар.

2. Квадрат берілген.Оның қанша симметрия осі, қанша симметрия центрі бар? Олар қалай орналасқан?

---

3. Координаталық жазықтықта А(2;1) және В(-3;-2) нүктелерінің симметрия осін салыңдар.

4. Координаталық жазықтықта төбелерінің координаталары А(2;4), В(-2;3), С(-4;6) болатын үшбұрышқа Ох осіне қарағанда симметриялы үшбұрыш салыңдар.

5.Нүктеге қарағанда симметриялы кесінділердің теңдігін дәлелдеңдер.

6. 2-Суретте көрсетілген фигураларды О нүктесінен айналдыра сағат тіліне қарсы 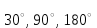және сағат тілі бағытында 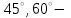қа бұрыңдар.



2-сурет

Осы типтегі тапсырмалар оқушыларды есептің шартын талдауға үйретеді; зерттеу іс-әрекетінің басты факторы ретінде танымдық іс-әрекеттің әдістері мен тәсілдерін қалыптастырады; танымның ішкі уәждерін дамытуға ықпал етеді; оқушылардың ойлау, зерттеу белсенділігін дамытуға; шығармашылық, зерттеушілік қызметін қалыптастыруға жағдай жасайды.

Сонымен қатар, зерттеп оқыту үдерісінде оқушылардың шығармашылық дағдыларын дамыту мақсатында төмендегі тақырыптар бойынша еркін тапсырма немесе эссе жазу жоспарын оқушыларға алдын-ала ұсыну қажет. Бұл жұмыс ізденіс белсенділігін арттыруға, зерттеу іс-әрекетін тиімді ұйымдастыруға, оқушылардың тақырыпты түсінуіне және оның уақытында қайталануына ықпал етеді.

1. Геометриялық түрлендіру туралы не білесіз?

2. Параллель көшіру математика тілінде.

2. Геометриялық түрлендіруді бейнелейтін өмірлік тәжірибеден мысал келтіріңіз: табиғатта, тұрмыста, техникада.

3. Геометриялық түрлендіруде еркін фигураны жасаңыз.

4. Табиғаттағы қозғалыстар.

5. Симметрия (өстік және центрлік) және оны адамның практикалық қызметінде қолдану.

Шеңберге іштей немесе сырттай сызылған үшбұрыштың ауданын пайдаланып шеңбердің радиусын табу. Алдымен шеңбер беріліп, оған іштей және сырттай үшбұрыш сызуға оқушыларды икемдеу керек. Яғни анықтама бойынша, егер үшбұрыштың барлық төбелері шеңберде жатса, онда ол шеңберге іштей сызылған болады.

Мұғалім-бағыттаушы: АВС үшбұрышы және оның төбелерін жанайтын шеңбер салыңыз. Оқушылар салынған шеңберлеріңіз үшбұрышқа сырттай сызылған ба әлде іштей сызылған ба? Бұл кезде берілетін жауаптар екі түрде болады. Біріншісі-іштей сызылған, екіншісі-сырттай сызылған. Негізгі жауап: үшбұрышқа сырттай сызылған шеңбер болады. Бірақ кей оқушылар іштей салып қоюы да мүмкін, оны тексеруді мұғалім ұмытпағаны жөн.

---

АВС үшбұрышына сырттай сызылған шеңбердің центрі О болса, онда ОА=OB=OC екені түсінікті. Неліктен OA=OB болғандығын сұраса кейбірі жауап беруге қиналуы мүмкін. Бұл интеллектуалды сұрақ болғаннан кейін проблемалық ахуалды субъекті мен объектінің өзара ерекше әсерлесуі, субъектінің тапсырманы орындау барысында өзінен талап етілген, субъектіге бұрыннан белгілі болып келген білімді игеру барысындағы байланысты анықтап, еске түсіру яғни математикалық құзіреттіліктің бірінші деңгейі қайта жаңғыртуда жатыр. Алайда олар оның себебі O нүктесі AB кесіндісінің ортасы арқылы өтетін перпендикулярдың бойында жатқандықтан және OB=OC үшін де дәл сол сияқты болатындығын түсіне бастайды. Сондықтан үшбұрышқа сырттай сызылған шеңбердің центрі оның қабырғаларының орталары арқылы жүргізілген перпендикулярлардың қиылысу нүктесінде болады деген тұжырымға келеді. Сөзіміз оқушыға түсінікті болу үшін, белгілеулер енгізуге кеңес береміз (3-сурет).



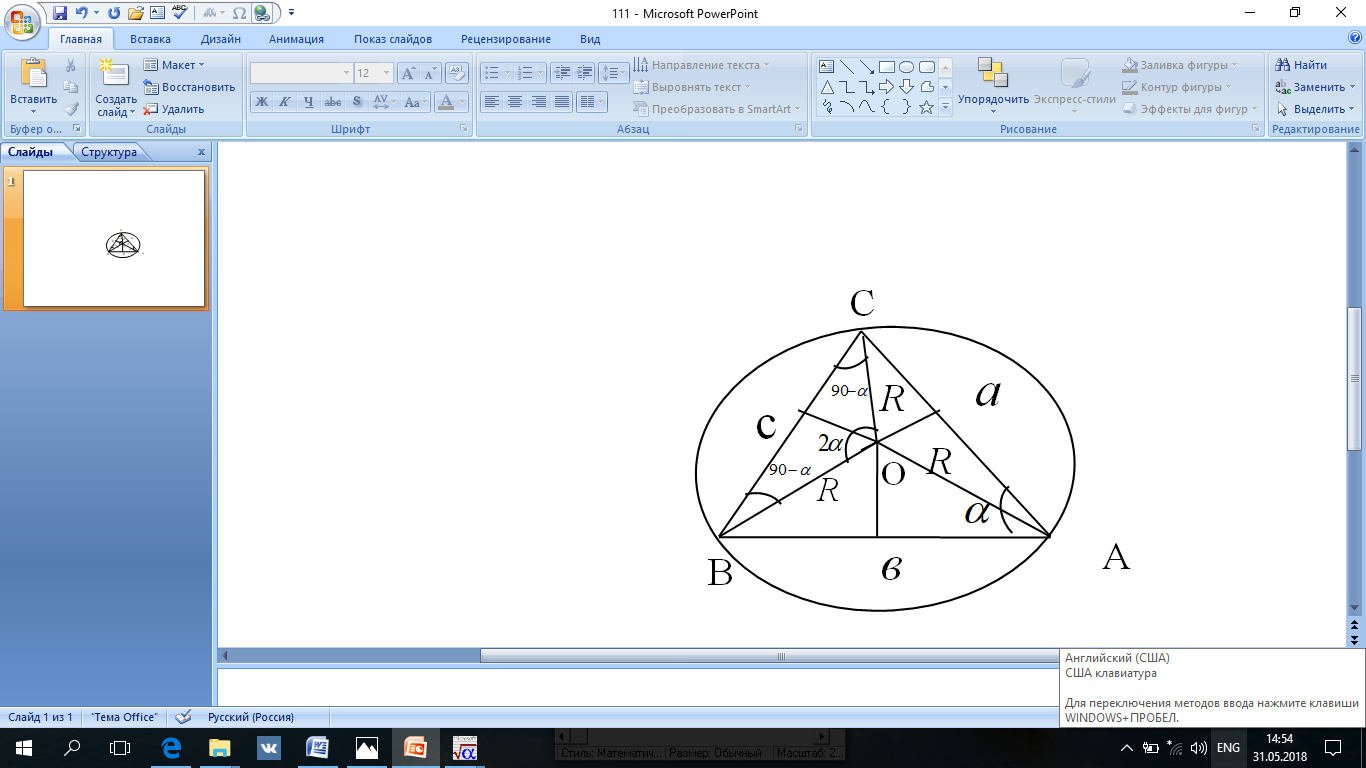
3-сурет

Оқушылар үшін бұрыннан таныс анықтамалар еске түсірілуі керек. Мысалы: іштей сызылған бұрыштың шамасы мен центрлік бұрыш шамасының арасындағы байланыс қандай? Олардың алдымен центрлік бұрыш анықтамасын қайталап, іштей сызылған бұрыш анықтамасын енгізіп, сонан соң есепке көшуіне жағдай жасау қажет.

Мәселені қою мен нақты ақпарат жинау бір мезетте іске аспайтыны белгілі. Суретте берілгендей оқушыларға іштей сызылған бұрыш анықтамасын тапқаннан кейін, олардың болжам жасауына мүмкіндік беруге болады. Мұғалімнің тарапынан: «үшбұрыштар тақырыбында өткізілген екі қабырғасы екі бұрышы бар ... қатынастардан құралған қандай теореманы естеріңе түсіреді?...» - деу арқылы ол қай теореманы меңзеп тұрғанын оқушылар болжап: «синустар немесе косинустар теоремасы»-деп немесе «Пифагор теоремасы» көмегімен деп жорамалдауы мүмкін. Олардың бұл жорамалдарына жауап ретінде Пифагор теоремасы тек тікбұрышты үшбұрыштарға, ал косинустар теоремасында екі қабырғасы және олардың арасындағы бұрышқа арналғандығын есептей отырып, жауаптың синустар теоремасы екендігін меңзейді. Оған көзі жеткен оқушы дереу ВОС үшбұрышының берілгендері дәл сондай екендігіне көзі жетіп қатынастарды жазуға кіріседі.

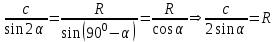(1)

Мұндағы 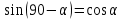екені белгілі. (1) өрнекті ықшамдауда,

---

Смотрите также файлы

• С ocacola classic (классическая кола).docx

• Курс на ускорение развития общества середины 1980х годов.docx

• Ваучерная приватизация особая форма безвозмездной приватизации государственной собственности по принципу "дележки" государственной собственности, предназначенной для приватизации, между всеми трудящимися.docx

• Существование общества невозможно без постоянного производства материальных благ и услуг.docx

• Благодаря своей относительной простоте применения, быстроте соединения различных материалов сварка находит широкое применение.docx