Тербелістердің ең қарапайым түрі гармоникалық тербелістер болып табылады. Гармоникалық тербелістер деп косинус (немесе синус) заңы бойынша өтетін процестерді айтады.

3.1 Еркін гармоникалық тербелістер

Гармоникалық тербелетін шама үшін өрнекті мына түрде жазуға болады:

. (3.1)

Мұндағы - тербеліс амплитудасы, өзгеретін шаманың ең үлкен мәні;

- меншікті циклдік жиілік, секунд ішінде өтетін толық тербелістер саны;

- кез-келген мезетінде мәнін анықтайтын тербеліс фазасы;

- бастапқы фаза, яғни бастапқы уақыт мезетінде тербеліс фазасы.

Толық тербеліс жасауға кететін уақыт период деп аталады , .

Бірлік уақыт ішінде жасалатын толық тербеліс саны жиілік деп аталады , .

Гармоникалық еркін тербелістер екінші реттік біртекті дифференциалдық теңдеумен сипатталады

. (3.2)

(3.2) теңдеуінің шешімі гармоникалық тербелістің теңдеуі (3.1) болып табылады.

Тербелмелі процестің физикалық табиғатына қарай тербелмелі процестер механикалық, электромагниттік, электромеханкалық, т.б. тербелістерге бөлінеді.

Т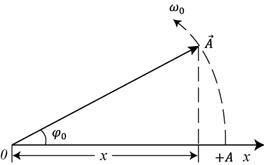 ербелмелі жүйе осциллятор, ал гармоникалық тербеліс жасайтын жүйені гармоникалық осциллятор деп атау қабылданған. Осцилляторларға маятниктер, тербелмелі контур, қатты денелердің молекулалары мен атомдары және т.б. жатады.

Гармоникалық тербеліс графикалық түрде кескіндеу үшін векторлық диаграмма әдісін қолданамыз (3.1 суретті қара).

3.1 cурет Тірек осі ретінде х осі алынады. Вектордың

ұзындығы тербеліс амплитудасына А тең, ал вектор мен х осінің арасындағы бұрыш тербелістің бастапқы фазасына тең. векторының оське проекциясы тербелетін шаманы көрсетеді. Егер осы векторды бұрыштық жылдамдықпен айналдырсақ, векторының оське проекциясы (3.1) теңдеуімен сипатталатын +А дан –А аралығында гармоникалық тербеліс жасайды. Осы тербелістердің циклдік жиілігі айналудың бұрыштық жылдамдығына тең.

3.2 Гармоникалық тербелістердің энергиясы

Механикалық тербелістердің толық энергиясы кинетикалық және потенциалдық энергиялардың қосындысы арқылы анықталады

, (3.3)

, (3.4)

. (3.5)

, және уақытқа тәуелділік графиктері 3.2 суретте көрсетілген.

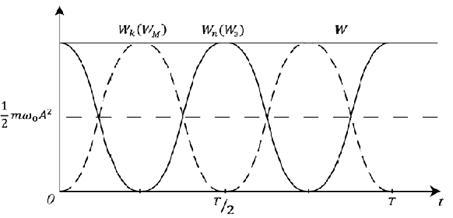
3.2 сурет

Тербелмелі контурда электромагниттік өрістің толық энергиясы . Конденсатордың зарядталуы кезінде оның астарларынынң арасында энергиясы электр өрісі пайда болады. Разрядталу кезінде индуктивті катушкада магнит өрісінің энергиясы пайда болады.

Магнит өрісінің энергиясы үшін

, (3.6) (3.6)

электр өрісінің энергиясы үшін

, (3.7)

және толық энергия

. (3.8)

(3.8)

4 Дәріс. Тербелістерді қосу. Өшетін және еріксіз тербелістер

Дәрістің мақсаты:

- бірдей бағыттағы және өзара перпендикуляр бағыттағы тербелістерді қосып үйрену;

- резонанс құбылысымен танысу.

Тербелмелі жүйенің бірмезгілде бірнеше тербелмелі процестерге қатысып, жүйеде өтетін қорытқы тербелістің заңдылығын анықтауды тербелістерді қосу деп қарастырады. Екі шекті жағдай қарастырылады: бірдей бағыттағы және өзара перпендикуляр бағыттағы тербелістерді қосу.

---

4.1 Бірдей бағыттағы тербелістерді қосу

Егер жүйе бірмезгілде:

, (4.1)

, (4.2)

т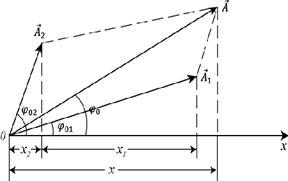 еңдеулерімен сипатталатын екі тербеліске қатысса, онда қосуды векторлық диаграмма әдісін қолданып, жүргізуге болады (4.1суретті қара). Қорытқы векторының х осіне проекциясы қосылғыш векторлардың проекцияларының қосындысына тең

4.1 сурет бойынша қорытқы вектор амплитудасын косинустар теоремасынан , (4.3)

ал қорытқы тербелістің бастапқы

фазасын . (4.4)

4.1 сурет

(4.1), (4.2) және (4.3) теңдеулерін талдайық.

4.1.1 Бірдей жиіліктегі және фаза ығысуы тербелістерді қосқанда қорытқы амплитуда . Тербелістер бірдей фазада (синфазды) тербеледі. Егер фаза ығысуы , онда , тербелістер қарама-қарсы фазада тербеледі. Екі жағдайда да қорытқы тербелістің амплитудасы уақыт бойынша өзгермейді. Егер екі тербеліс фаза айырмасы тұрақты болып, уақыт бойынша үйлесімді өтетін болса, оларды когеренттік тербелістер деп атайды.

4.1.2 Жиіліктері әртүрлі тербелістерді қосқанда және векторлары әртүрлі бұрыштық жылдамдыққа ие болады. Қорытқы векторы шама жағынан өзгереді және айнымалы жылдамдықпен айналады. Бұл тербелістер когерентті емес, гармоникалық емес, күрделі құбылыс байқалады.

4.1.3 Бірдей бағыттағы, бірақ жиіліктері ұқсас тербелістерді қосқанда, амплитудасы периодты түрде өзгеретін тербеліс пайда болады. Мұндай тербелістер соғу деп аталады.

Бір тербелістің жиілігі , ал екіншісінің жиілігі , бастапқы фазалары нөлге тең, амплитудалары тең болсын, онда ,

. Қорытқы тербеліс

(4.5)

түрінде жазылады.

шамасы 0 ден 2 А-ға дейінгі аралықта соғудың циклдік жиілігі деп аталатын циклдік жиілікпен өзгереді. Соғудың жиілігі болғандықтан, жоғарыда көрсетілген айнымалы шаманы соғудың амплитудасы (шартты) деп атайды. Соғудың периоды .

4.2 Өзара перпендикуляр тербелістерді қосу

Егер тербелістер бір мезгілде х осі және у осі бойымен өтсе, онда олардың теңдеулері келесі түрде жазылуы мүмкін

, , (4.6)

мұндағы - екі тербелістің фазалар айырымы (фаза ығысуы).

Мұндай тербелістерді осциллографтың горизонталь және вертикаль басқарушы пластиналарына периодты гармоникалық сигналдар берген кезде бақылауға болады. Қорытқы тербелістің траекториясын анықтау үшін (4.6) теңдеудегі уақыттан арылу қажет. Ол үшін және , өрнектеуіміз қажет.

(4.6) теңдеудегі уақыттан құтылып, траекторияның теңдеуін шығарып аламыз

. (4.7)

4.1 кесте

Фазалар айырымы	Траектория теңдеуі	Графиктік кескінделуі

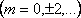
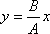
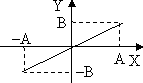
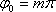
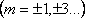
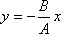
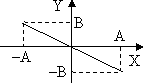
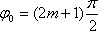
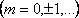
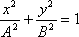
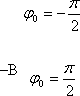
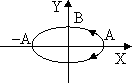
(4.7) теңдеу жарты осьтері кез келген бағытта орналасқан эллипстің теңдеуін береді. Осы теңдеуден шығатын дербес жағдайлар 4.1 кестеде көрсетілген.

Егер өзара перпендикуляр тербелістердің жиіліктері бірдей болмаса, онда қорытқы қозғалыстың траекториялары Лиссажу фигуралары деп аталатын күрделі қисықтарды береді.

---

4.3 Еркін өшетін электрмагниттік тербелістер

Өшпейтін тербелістер идеал жүйелерде ғана өтеді. Бұл жүйелерде энергия шығыны ескерілмейді. Бірақ кез келген реалды процестерде энергия шығынынан құтылу мүмкін емес, тербелмелі контурда энергия шығыны электр кедергісінің болуына байланысты туындайды.

Нақты тербелмелі контурдың идеал контурдан ерекшелігі - конденсатор мен катушкаға кедергісі R резистор тізбектей жалғанған.

R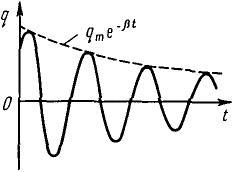 кедергіні ескеріп, тізбектің 1-2 бөлігі үшін жалпылама Ом заңы :

,

мұндағы , ,

онда

, (4.8)

мұндағы - өшу коэффициенті, .

4.2 сурет

(4.8) теңдеуі – өшетін тербелістердің екінші ретті дифференциалдық теңдеуі.

(4.8) теңдеуінің шешімі өшетін тербелістің теңдеуі болып табылады,

, (4.9)

мұндағы тұрақты (бастапқы амплитуда) және (бастапқы фаза) бастапқы шарттарға тәуелді. тәуелділік графигі 4.2 суретте көрсетілген. Өшетін тербелістер периодты емес, себебі тербелетін шама, мысалы берілген жағдайда зарядтың максимал мәні еш қайталанбайды, бірақ бірдей тең уақыт аралығында

(4.10)

және бірдей жиілікпен

(4.11)

максимал және минимал мәндеріне ие болады. Сондықтан және шамаларын өшетін тербелістің шартты периоды және шартты циклдік жиілігі деп атайды.

Енгізілген шамаларды қолданып, электрмагнитік өшетін тербелістердің периоды мен жиілігін

және (4.12)

түрінде жазуға болады.

Өшетін тербелістің амплитудасы есе азаятын уақыт аралағын орнығу уақыты деп атайды.

Өшетін тербелістің амплитудасының кему жылдамдығын сандық түрде сипаттау үшін өшудің логарифмдік декременті деген ұғымды қолданады. Өшудің логарифмдік декременті деп бір периодқа ерекшеленетін уақыт мезеттеріне сәйкес амплитудалардың мәндерінің қатынасының натурал логарифмін айтады:

, (4.13)

мұндағы - амплитудасы есе азаятын уақыт аралығында жасайтын тербеліс саны.

Нақты тербелмелі контур кез келген уақыт мезетінде жүйе тербелісінің энергиясының өшетін тербелістің шартты период аралығында осы энергияның шығынына қатынасының -ге көбейтіндісіне тең сапалылықпен сипатталады

.

Контурдың сапалылығы

, (4.14)

яғни контурдың сапалылығы тербеліс амплитудасы есе азайғандағы тербеліс саны көп болған сайын жоғары болады.

4.4 Еріксіз электрмагниттік тербелістер. Резонанс

Еріксіз электрмагниттік тербелістерді тудыру үшін контурдың элементтерін айнымалы ЭҚК-не қосу қажет:

.

Берілген жағдайда тербелмелі контурдың теңдеуі келесі түрде жазылады

немесе

. (4.15)

Еріксіз тербелістер жағдайында бізді орныққан тербелістер қызықтыратындықтан, бұл теңдеудің дербес шешімі

, (4.16)

мұндағы - конденсатордағы зарядтың амплитудасы;

- заряд пен сыртқы ЭҚК тербелістері арасындағы фаза айырмасы.

(4.16) теңдеуді бойынша дифференциалдап, контурдағы ток күшін аламыз:

. (4.17)

(4.16)-ны тағы да бойынша дифференциалдап, жазамыз

. (4.18)

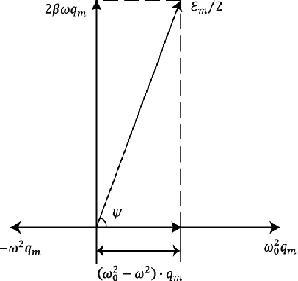( 4.16)-(4.18) теңдеулерді (4.15)-ке қойып -ң фаза ығысуы бар бір жиіліктегі үш тербелістің қосындысы екенін көруге болады. Бұл тербелістерді қосудың векторлық диаграммасы 4.3 суретте көрсетілген.

---

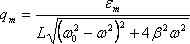, (4.19)

.

4.3 сурет

Егер , екенін ескерсек,

онда ,

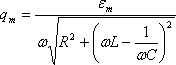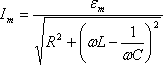. (4.20)

(4.19) өрнегі берілген мәндерінде зарядтың еріксіз тербелісінің амплитудасы (және фазасы) ЭҚК-ң жиілігімен анықталатынын көрсетеді. Меншікті жиілік пен айнымалы ЭҚК жиілігінің айырмасы неғұрлым аз болған сайын, амплитуда соғұрлым жоғары болады. Сыртқы әсер жиілігінің белгілі бір мәнінде еріксіз тербелістің амплитудасының күрт артуы резонанс деп аталады. Резонанс басталатын сыртқы әсердің (ЭҚК) жиілігі резонанстық жиілік деп аталады.

Заряд (конденсатордағы кернеу) және ток күші үшін резонанстық жиіліктер келесі формулалармен анықталады:

,

. (4.21)

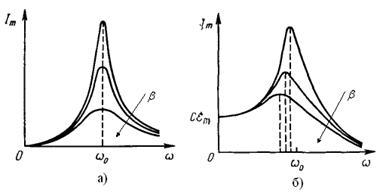
4.4 сурет

және ток үшін 4.4 а,б суретте резонанстық қисықтар көрсетілген. -ң мәні аз болған сайын (актив кедергі аз болған сайын), резонанс кезіндегі максимум жоғарылап, ұштана түседі. кезде кернеуге арналған резонанстық қисықтардың ток күшінің резонанстық қисықтарынан айырмашылығы, олар нүктесінде тоғысады, - конденсаторды тұрақты кернеу көзіне жалғағанда конденсаторда пайда болатын кернеу.

Электр тербелістерін қарастырғанда тұрақты ток үшін жазылған жалпылама Ом заңы қолданылды. Бұл тізбекте жарық жылдамдығына тең жылдамдықпен таралатын электромагниттік әсерлер кезінде мүмкін болады. Сондықтан, егер контурдың сызықтық өлшемдері аса үлкен болмаса ( , - контурдағы тербеліс жиілігі), онда әр уақыт мезетінде контурдың барлық бөліктерінде ток күші бірдей деп есептеуге болады. Мұндай айнымалы токты квазистационар ток деп атайды.

5 Дәріс. Толқындық процестер

Дәрістің мақсаты:

- толқынның түрлерін оқып-үйрену;

- толқынның энергиясы, энергия ағыны, Умов векторы, толқынның қарқындылығы ұғымдарымен танысу.

5.1 Серпімді толқындар

Кез келген ортаның бір нүктесінде пайда болатын тербелістер шекті жылдамдықпен тарайды. Тербеліс көзінен алысырақ орналасқан нүктелерге тербеліс кешігіп жетеді. Тербелістің біртұтас ортада таралу процесі толқын деп аталады. Толқын таралғанда, орта бөлшектері орын ауыстырмайды, тепе-теңдік маңында тербеледі. Сондықтан барлық толқындарға тән қасиет – толқындық процесте зат тасымалы болмайды, энергия ғана тасымалданады. Серпімді ортада таралатын механикалық тербелістер серпімді толқындар деп аталады.

Серпімді толқындар бойлық және көлденең болып екіге бөлінеді. Бойлық толқындарда орта бөлшектері толқынның таралу бағытымен тербеледі. Ал көлденең толқындарда орта бөлшектері толқынның таралу бағытына препендикуляр жазықтықта тербеледі.

Тербеліс уақыт мезетінде жететін нүктелердің геометриялық орны толқындық бет деп аталады. Толқындық беттің пішініне қарай толқындар жазық немесе сфералық болуы мүмкін.

Толқын келесі параметрлермен сипатталады: - бірдей фазада тербелетін жақын бөлшектер арақашықтығы толқын ұзындығы деп аталады; - период, бір тербелістің уақыты; - жиілік, бірлік уақыт ішіндегі тербеліс саны. Олардың арасындағы байланыс:

---

, .

5.2 Толқындық теңдеу

Толқынның теңдеуі уақыт пен кеңістіктікке тәуелді функция болып табылады. осі бойымен ауытқулар таралғанда, орта бөлшегінің тепе-теңдіктен ығысуы координата мен уақыттың функциясы болып есептеледі, яғни .

Егер тербеліс көзі жазықтығында жататын нүктелердің тербелісі функциясымен сипатталса, онда тербеліс көзінен қандай да бір қашықтықта орналасқан бөлшектерге тербеліс уақытқа кешігеді, мұндағы - толқынның таралу жылдамдығы. қашықтықта орналасқан орта бөлшектерінің тербеліс теңдеуі

.

Толқындарды сипаттау үшін толқындық сан қолданылады

. (5.1)

Толқындық сан ұзындығы тең кесіндіге қанша толқын ұзындығы сәйкес келетінін көрсетеді.

Ендеше

, (5.2)

мұндағы - толқынның бастапқы фазасы;

- жазық толқынның фазасы.

(5.2) теңдеуі – осінің бойымен таралатын жазық толқынның теңдеуі.

Толқын фронтына перпендикуляр бағытталған бірлік вектормен сипатталатын кез келген бағытта жазық толқын таралғанда толқындық вектор енгізеді

.

Бұл жағдайда жазық толқынның теңдеуі келесі түрде жазылады:

,

мұндағы .

5.3 Толқындық теңдеу

Материялық нүктенің барлық мүмкін болатын қозғалыстарын сипаттайтын динамиканың негізгі теңдеуі сияқты толқындық процестер үшін де толқынның түріне тәуелсіз теңдеулер бар. Бұл теңдеулер - толқынды сипаттайтын, кеңістік пен уақыттағы функцияның өзгерісін байланыстыратын дербес туынды түріндегі дифференциалдық теңдеулер.

Оларды толқындық теңдеулер деп атайды. Толқындық теңдеуді алу үшін (5.2) теңдеуді алдымен уақыт бойынша, сосын х бойынша екі рет дифференциал аламыз. Нәтижесінде

, .

Бірінші теңдеуді екінші теңдеуге қойып, х осі бойымен жазық толқынның теңдеуін аламыз:

. (5.3)

(5.2) жазық толқынның теңдеуі (5.3) толқындық теңдеудің шешімі болып табылады.

Жалпы жағдайда, ығысу төрт айнымалының функциясы болып табылады және ол келесі түрде жазылады

, (5.4)

мұндағы

.

5.4 Толқынның энергиясы. Умов векторы

Кеңістікте энергия тасымалдайтын толқындар қума толқындар деп аталады. Толқын таралатын серпімді орта бөлшектердің тербелмелі қозғалысының кинетикалық энергиясына және ортаның деформациясынан пайда болатын потенциалдық энергияға ие болады.

Барлық нүктелерде қозғалыс жылдамдығы және деформациясын бірдей ( және ) деп есептеуге болатын және сәйкесінше х осі бойынша таралатын толқын үшін болатын аз көлемді ойша белгілеп аламыз.

Белгіленген көлем кинетикалық энергияға ие, мұндағы - көлемдегі заттың массасы, .

Теңдеуге , мәнін қойып, келесі өрнекті аламыз

.

Қарастырылып отырған көлем потенциалдық энергияға ие

,

мұндағы - Юнг модулі;

- салыстырмалы ұзару немесе сығылу. Қума толқындардың жылдамдығы мен екенін ескерсек, потенциалдық энергияның өрнегін аламыз

.

Толық энергия мен қосындысына тең

. (5.5)

Осы энергияны көлемге бөлсек, энергия тығыздығын аламыз

.

Сонымен ортаның әрбір нүктесінде энергияның орташа тығыздығы

---

Смотрите также файлы

• Физика дәріс.docx

• Философия методичка рус.doc

• Философия.docx

• Электротехникалық материалтану зертаханалық жұмыс 3,4.docx

• Электростатика.doc