Файл: Уравнения с одной переменной.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 08.11.2023

Просмотров: 41

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.


2 = 6x - 20

Дополним ОДЗ: 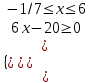; 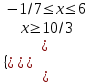 10/3  х  6.

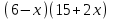= 9x2 - 60х + 100

11x2 - 57х + 10 = 0, x = 2/11; 5

x = 2/11ОДЗ. Отв. 5

16) 3 – x =

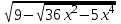
ОДЗ: 3 – x ≥ 0, x  3

9 – 6x + x2 = 9 - 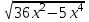, 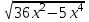= 6x - x2

Дополним ОДЗ: ; ; 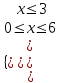 0  х  3

36x2 - 5х4 = 36x2 - 12х3 + х4, 6x4 - 12х3 = 0

6х3(х - 2) = 0, x = 0; 2. Отв. 0; 2

17) (x - 4) 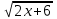= 0

a) 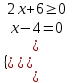; ; 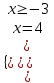х = 4

б) 2х + 6 = 0, х = -3. Отв. -3; 4

18) (2x - 3) 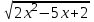= 0

a) 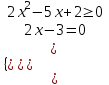; 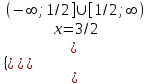 нет корней

б) 2х2 – 5х + 2 = 0, х = 1/2; 2, Отв. 1/2; 2

19) (2x - 3) 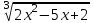= 0

a) 2x – 3 = 0, х = 3/2

б) 2х2 – 5х + 2 = 0, х = 1/2; 2, Отв. 1/2; 3/2; 2
II. Введение новой переменной

1) 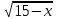+ 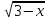= 6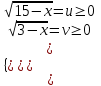

; ; ; ;


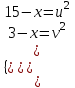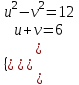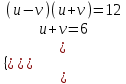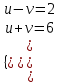
2u = 8, u = 4, = 4, 15 – x = 16, x = -1. Отв. -1

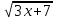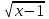2) - = 2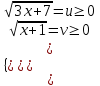

; ; ; ;

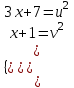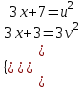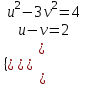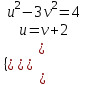
(v + 2)2 – 3v2 = 4, 2v(v – 2) = 0, v = 0; 2

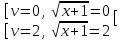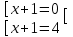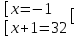; ; . Отв. -1; 3

3) 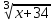- 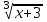= 1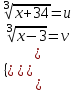

; ; ; ; ;

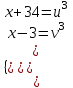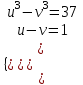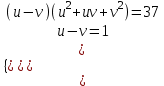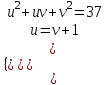(v + 1)2 + (v+ 1)v+ v2 = 37, v2 + v – 12 = 0, v = -4; 3

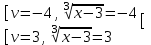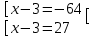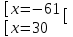; ; . Отв. -61; 30

4) x3 + 3x – 18 + 4 ,

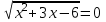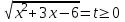
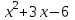= t2, 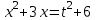, t2 + 6 – 18 + 4t = 0

t2 + 4t - 12= 0, t = -6; 2, t = -6 (исключаем)

t = 2, 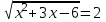, 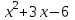= 4, ,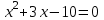

х = -5; 2. Отв. -5; 2

5) 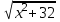- 2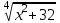
= 3,

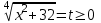
t2 - 2t - 3= 0, t = -1; 3, t = -1 (исключаем)

t = 3, 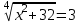, , 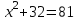, 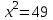х = ±7. Отв. ±7.

6) x2 + ,

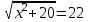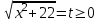
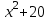= t2, 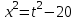, t2 – 20 + t = 22, t2 + t - 42= 0,

t = -7; 6, t = -7 (исключаем)

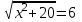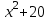t = 6, , = 36, ,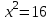

х = ±4. Отв. ±4.

7) 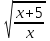+ 4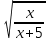 - 4 = 0,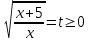

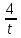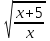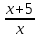t + - 4 = 0, t2 - 4t + 4 = 0, t = 2, = 2, = 4

х ≠ 0, х + 5 = 4x; x = 5/3. Отв. 5/3.

8) 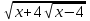+ 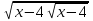= 6, t = 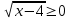, х = t2 + 4

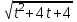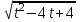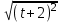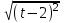+ = + = |t + 2| + |t - 2|

Получили |t + 2| + |t - 2| = 4

t 0  t + 2  0  |t + 2| = t + 2

t + 2 + |t - 2| = 4, t - 2| = 2 - t

2 - t  0, t  2, t - 2  0  t - 2| = 2 – t. Получили

t + 2 + 2 – t = 4, 0 = 0 (истина)  0  t 2 – решение

0 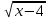  2, 0  х - 4 4, 4  х  8. Отв. 4; 8

9)
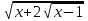
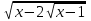+ = 2, t = 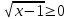, t2 = x – 1, х = t2 + 1

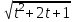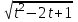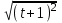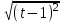+ = + = |t + 1| + |t - 1|

Получили |t + 1| + |t - 1| = 2

t 0  t + 1  0  |t + 1| = t + 1

t + 1 + |t - 1| = 2, |t - 1| = 1 - t

1 - t  0, t  1, t - 1  0  |t - 1| = 1 – t. Получили

t + 1 + 1 – t = 2, 0 = 0 (истина)  0  t 1 – решение

0 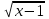  1, 0  х - 1 4, 1  х  2. Отв. 1; 2

10) 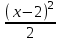+ 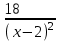= 7(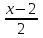 - 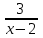) + 10

t = 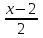- 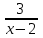; t2 = 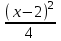+ 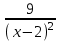- 3. Имеем:

2(t2 + 3) = 7t + 10, 2t2 - 7t - 4 = 0, t = -1/2; 4



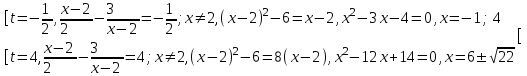
Отв. -1; 4 и

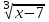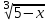11) + = 1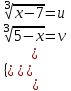

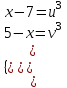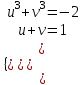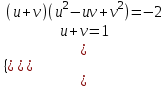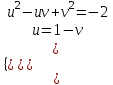; ; ; ; ; (1 - v)2 - (1 - v)v+ v2 = -2, 3v2 - 3v + 1 = 0

D = 9 – 12 < 0 – корней нет.

Системы алгебраических уравнений

Решением системы уравнений с двумя неизвестными называется пара значений неизвестных (х, у), обращающая каждое уравнение системы в верное равенство.

I. Метод подстановки

а) выразить одну переменную через другую из какого-либо уравнения системы;

б) найденное выражение подставить в другое уравнение системы;

в) найти корни полученного уравнения.

1) ; ;

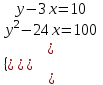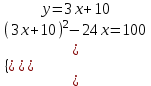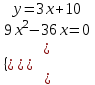
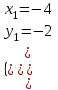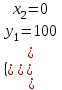; . Отв. (-4;-2); (0; 100).

II. Метод алгебраического сложения

а) уравнения системы сложить почленно, предварительно умножив каждое из них на такое число, чтобы в результате исключается одна из переменных;

б) решить полученное уравнение;

в) найти соответствующие значения другой переменной.

1) 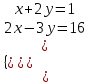; ; 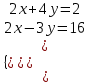; 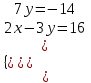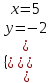. Отв. (5;-2).

2) ;

;

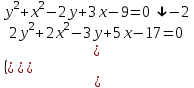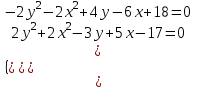
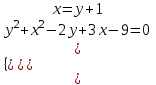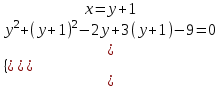
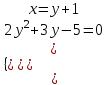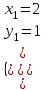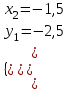; ; . Отв. (2; 1); (-1,5; -2,5).
III. Метод введения новой переменной

Смотрите также файлы