4) Решить систему

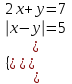
|x - y| = 5  x – y = 5, либо x – y =- 5

а) 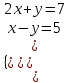; ; 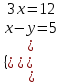x= 4, y = -1, (4;-1)

б) 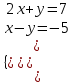; ; 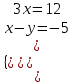x= 2/3, y = 17/3, (2/3; 17/3)

Отв. (4;-1); (2/3; 17/3)

II. Для решения уравнения: |f(x)| = g(x) используются два способа

а) Уравнение: |f(x)| = g(x) равносильно совокупности системы:

, либо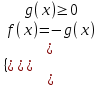

б) Уравнение: |f(x)| = g(x) равносильно совокупности системы:

, либо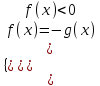

Выбор способов а) или б) зависит от того, какое из неравенств g(x) ≥ 0 или f(x) ≥ 0 легче решить.

1) |x - 4| = 4x + 1 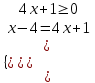 , либо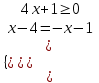

а) 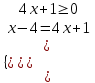; ; 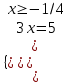x = -5/3 – нет решения

б) 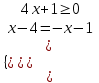; ; 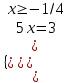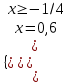. Отв. 0,6

2) |x² - 9| = 8x 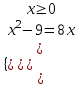 , либо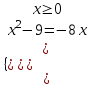

а) 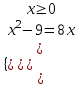; ;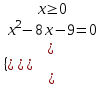 ; 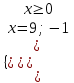x = 9

б) 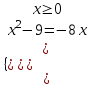; ;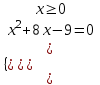 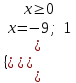, x = 1

Отв. 1; 9

3) |x² - 3| = 3x² - 1. Обозначим x² = t ≥ 0

|t - 3| = 3t - 1 

---

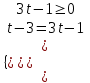
, либо

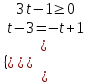
а) ; ;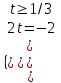 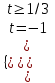- нет решения

б) 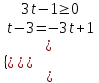; ;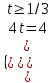 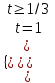, t = 1, x² = 1, x = 1. Отв. 1

4) | 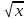- 3| = 3 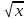+ 1. Обозначим 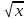= t ≥ 0

|t - 3| = 3t + 1 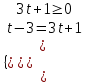 , либо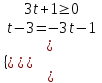

а) 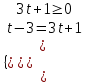; ;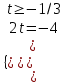 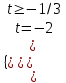- нет решения

б) 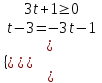; ;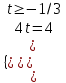 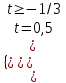, t = 0,5, 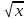= 0,5, x = 0,25. Отв. 0,25

5) x² + 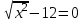, x² + |x| - 12 = 0, |x| = t ≥ 0

t² + t - 12 = 0, t = -4; 3, t = -4 – исключаем

t = 3, |x| = 3, x = 3. Отв. 3

6) x² + 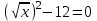, ОДЗ: х ≥ 0,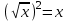

x² + x - 12 = 0, x = -4; 3, x = -4 – исключаем. Отв. 3

7) x² + 1 +|x- 1| = 2|x|, Поскольку x² = |x|², то

x² + 1 +|x- 1| = 2|x|, (x² - 2|x| + 1) + |x- 1| = 0, (|x|² - 1)² + |x- 1| = 0

(|x|² - 1)² ≥ 0 и |x- 1| ≥ 0  

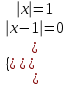
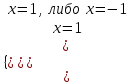
х = 1. Отв. 1

8) |3x- 4| =4x² + 3х - 2. Поскольку функция, стоящая под модулем проще, то при решении исходного уравнения переходим к совокупности систем

---

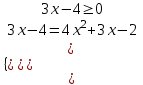, либо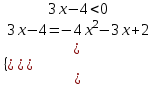

а) ;

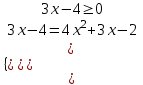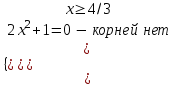
б) ; ;

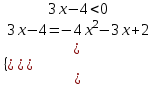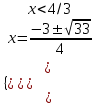
Отв.

---

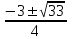
III. Уравнение: |f(x)| = |g(x)|  f²(x) = g²(x)  (f(x) - g(x))(f(x) + g(x)) = 0,

т.е. f(x) = g(x), либо f(x) = - g(x).

1) |2x+ 5| = |x - 1|  2x + 5 = x – 1, либо 2x + 5 = -x+1

а) 2x + 5 = x – 1, х =-6

б) 2x + 5 = -x+1, х =-4/3

Отв. -6; -4/3
IV. Метод областей

1) |x - 7| + |9 + x| = 18

|x - 7| = 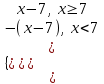; |9 + x| =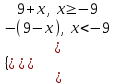


x < -9
Граничные точки -9 и 7 разбивают числовую ось на три области

x ≥ 7 -9  x < 7 7 -9

Определим знаки каждого из выражений, стоящих под знаком модуля в каждой области. Составим таблицу знаков

	x < -9	-9  x < 7	x ≥ 7
x - 7	-	-	+
9 + x	-	+	+

I обл. x < -9

-(x – 7) – (9 + x) = 18, х = -10I обл.

II обл. -9  x < 7

-(x – 7) + (9 + x) = 18, 16 = 18 (ложь) – нет решения

III обл. x ≥ 7

x – 7 + 9 + x = 18, х = 8III обл. Отв. -10; 8

2) |x+ 1| - |2x- 3| = x- 5

|x+ 1| = 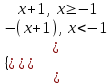; |2x- 3| =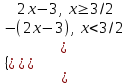

---

x < -1
Граничные точки -1 и 3/2 разбивают числовую ось на три области

x ≥ 3/2 -1  x < 3/2 3/2 -1

Определим знаки каждого из выражений, стоящих под знаком модуля в каждой области. Составим таблицу знаков

	x < -1	-1  x < 3/2	x ≥ 3/2
x + 1	-	+	+
2x + 3	-	-	+

I обл. x < -1

-x – 1 + 2x- 3 = x - 5, 0 = 4 (ложь) – нет решения

II обл. -1  x < 3/2

x + 1 + 2x- 3 = x - 5, х = -3/2II обл.

III обл. x ≥ 3/2

x+ 1 - 2x + 3 = x - 5, х = 9/2III обл. Отв. 9/2

---

Смотрите также файлы

• Император Акихито родился 23 декабря 1933 года в Токио, Япония. Он был первым сыном Императора Хирохито и Императрицы Нагако. В 1959 году Акихито женился на Мичико Шода, дочери бывшего председателя торговой компании.docx

• Выберите все верные ответы. В каких нормативноправовых документах определена государственная политика в сфере образования в области воспитания и сохранения традиционных для нашего общества ценностей.doc

• Wretched, beastly.doc

• Теоретические аспекты формирования и использования финансовых ресурсов бюджетных организаций.pptx

• Отчет о практическом занятии 1 Тема Установка и настройка по open Server Panel. Цель Установить и настроить по open Server Panel.docx