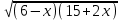ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 39
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
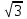
2) x - 11
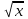– 12 = 0, 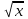= t ≥ 0t2 – 11t - 12 = 0, t= -1; 12, t= -1 – исключаем
t= 12,
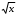= 12, х = 144.3) (х + 3)4 + 3х2 + 18х – 1 = 0, (х + 3)4 = ((х + 3)2)2
Заметим, что
(х + 3)2 = х2 + 6х + 9
3х2 + 18х = 3(х2 + 6х)
х2 + 6х = t, тогда (t + 9)2 + 3t – 1 = 0, t2 + 21t+ 80 = 0, t = -16; -5
t = -16, х2 + 6х = -16, x2 + 6x + 16 = 0, D = 36 - 64 < 0 – нет корней.
t = -5, х2 + 6х = -5, х2 + 6х + 6= 0, х = -5; -1.
4) (2x2 – 3x + 1)(2x2 + 5x + 1) = 9x2.
Устанавливаем, что х = 0 не является решением уравнения.
х(2x – 3 +
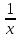)х(2x + 5 + 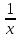) = 9x2, (2x – 3 + 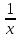)(2x + 5 + 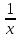) = 9.2x +
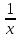- 3 = t, t(t + 8) = 9, t2 + 8t - 9 = 0, t = 1; -9.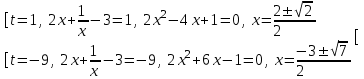
5) (x+2)(x+12)(x+3)(x+8) = 4x2, (x2 + 14x + 24)(x2 + 11x + 24) = 4x2.
х = 0 не является решением уравнения.
х(x +
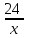+ 14)х(x + 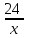+ 11) = 4x2, (x + 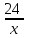+ 14)(x + 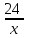+ 11) = 4.x +
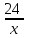+ 11 = t, t(t + 3) = 4, t2 + 3t - 4 = 0, t = 1; -4.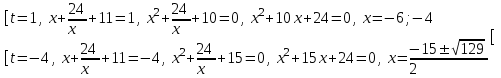
6) x4 – 3x3 - 8x2 + 12x + 16 = 0
х = 0 не является решением уравнения.
x2 – 3x - 8 +
+ 
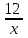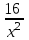
= 0, x2 +
- 3(x - 
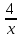) – 8 = 0x -
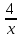= t, (x - 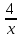)2 = x2 – 8 + = t2, x2 + = t2 + 8, тогдаt2 + 8 - 3t - 8 = 0,t(t – 8) = 0, t = 0; 3.
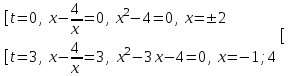
II. Метод разложения на множители.
1) x3 – 5x2 – 10x + 50 = 0
(x3 – 5x2) – (10x – 50) = 0, x2(x – 5) – 10∙(x – 5) = 0, (x – 5)(x2 - 10) = 0
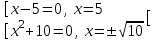
Иррациональные уравнения
Иррациональным уравнением называется уравнение, в котором переменная содержится под знаком корня или под знаком операции возведения в дробную степень.
Решение иррационального уравнения сводится к переходе от иррационального уравнения к рациональному уравнению путем возведения в степень обеих частей уравнения или замены переменной. Причем возведение в нечетную степень является равносильным преобразованием при любых значений правой части, а возведение в четную степень является равносильным преобразованием только в случае положительности правой части уравнения.
При возведении обеих частей уравнения возможны появление посторонних корней, поэтому их решение предполагает два подхода:
1) решение без равносильных преобразований, но при этом необходимо проверка;
2) использование равносильных преобразований.
К основным методам решения иррациональных уравнений относятся:
I. Возведение обеих частей уравнений в одну и туже степень
а)
; 
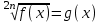
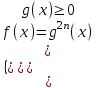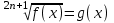f(x) = g2n+1(x)В частности для n = 1 имеем:
; 
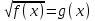
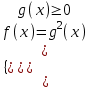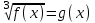f(x) = g3(x).б)
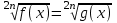
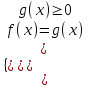
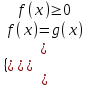
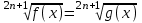f(x) = g(x)В частности для n = 1 имеем:
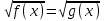
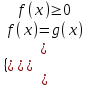
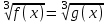f(x) = g(x).в)
; 
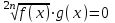
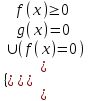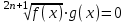
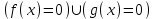
В частности для n = 1 имеем:
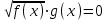
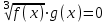
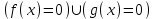.Замечание. При решении иррациональных уравнений с четной степенью можно выделить ОДЗ уравнения. Например, уравнение
запишем: ОДЗ: g(x) ≥ 0
f(x) = g2(x).
Упр. Решить уравнение
1)
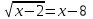
ОДЗ: x - 8 ≥ 0, x ≥ 8, x - 2 = (x - 8)2, x - 2 = x2 – 16х + 64, x2 – 17х + 66 = 0
D = 289 – 264 = 25, x = 6; 11. x = 6ОДЗ. Отв. 11
2)
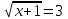
ОДЗ: g(x) = 3 > 0 – есть корни
x + 1 = 9, x = 8. Отв. 8
3)
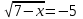, g(x) = -5 < 0 – нет корней4)
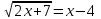
ОДЗ: x - 4 ≥ 0, x ≥ 4
2x + 7 = (x - 4)2, x2 – 10х + 9 = 0, x = 1; 9
x = 12ОДЗ. Отв. 9
5) x +
, 
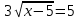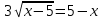
ОДЗ: 5 - x ≥ 0, x 5
9(x - 5) = (5 -x)2, x2 – 19х + 70 = 0, x = 5; 14
x = 14ОДЗ. Отв. 5
6)
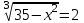, 35 – x2 = 8, x2 = 27, x = ±
= ±
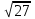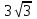
Отв. ±
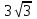
7)
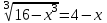, 16 – x3 = (4 - х)3, 16 – x3 = 64 – 48х2 + 12х – х312x2 – 48х + 48 = 0, x2 – 4х + 4 = 0, х = 2. Отв. 2
8)
, 
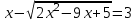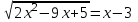
ОДЗ: x- 3 ≥ 0, x ≥ 3
2x2 – 9х + 5 = x2 – 6х + 9, x2 – 3х – 4 = 0, x = -1; 4
x = -1ОДЗ. Отв. 4
9)
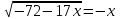, ОДЗ: -x ≥ 0, x 0
-72 – 17х = x2, x2 + 17х + 72 = 0, x = -9; -8. Отв. -9; -8.
10)
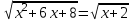
ОДЗ: x+ 2 ≥ 0, x ≥ -2
x2 + 6х + 8 = х + 2, x2 + 5х – 6 = 0, x = -3; -2
x = -3ОДЗ. Отв. -2
11)
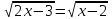
ОДЗ: x- 2 ≥ 0, x ≥ 2
2х – 3 = х - 2, x = 1ОДЗ. Отв. нет корней
12)
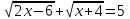
ОДЗ:
; 
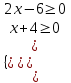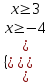х ≥ 3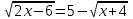
2х – 6 = 25 -
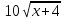+ х – 4 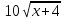= 35 – хДополним ОДЗ:
; 
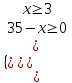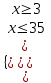3 х 35.100(х + 4) = (35 – х)2; x2 - 170х + 825 = 0, x = 5; 165
x = 165ОДЗ. Отв. 5
13)
= 
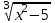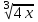, x2 – 5 = 4х, x2 - 4х - 5 = 0, x =-1; 5. Отв. -1; 514)
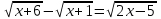
ОДЗ:
; 
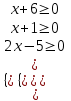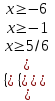х ≥ 5/6x – 6 - 2
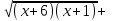x + 1 = 2x– 5, 
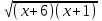= 6x2 + 7х + 6 = 36, x2 + 7х - 30 = 0, x = 3; -10
x = -10ОДЗ. Отв. 3
15)
, 
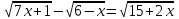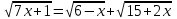
ОДЗ:
; 
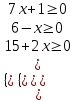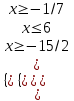-1/7 х 6.7x + 1 = 6 – x + 15 + 2x + 2
