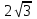ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 40
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
1)
; 
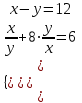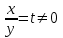, t +
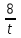= 6, t2 – 6t + 8 = 0, t = 2; 4а) t = 2,
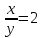, x = 2y, 
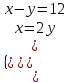; 2y – y = 12, y = 12, x = 24, (24; 12)б) t = 4,
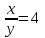, x = 4y, 
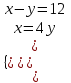; 4y – y = 12, y = 4, x = 16, (16; 4)Отв. (24; 12); (16; 4).
2)
; 
, 
; 
; 
; 
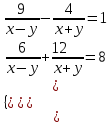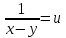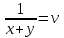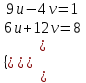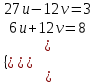
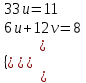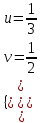
u =
, 
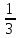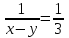, x – y = 3v =
, 
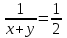, x + y = 2
, 
, 
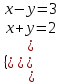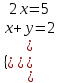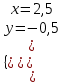. Отв. (2,5;-0,5).3)
; 
; 
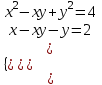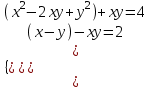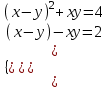; x – y = u, xy = v
; 
; 
; 
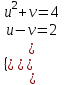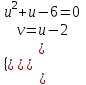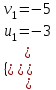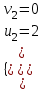; (u, v) = (-3; -5), (2; 0)а) (u, v) = (2; 0)
; 
; 
;
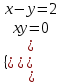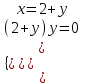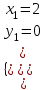
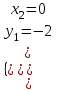; (2; 0); (0; -2).б) (u, v) = (-3; -5)
; 
; 
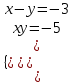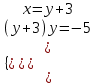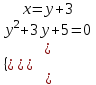, D= 9 – 20 < 0 – нет решенийОтв. (2; 0); (0; -2).
4)
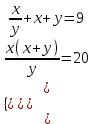;; x + y = u,
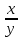= v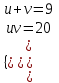
; 
; 
; 
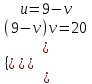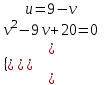
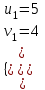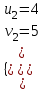; (u, v) = (5; 4), (4; 5)а) (u, v) = (5; 4)
;
; 
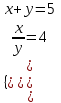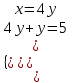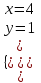; (4; 1).б) (u, v) = (4; 5)
;
; 
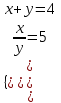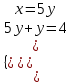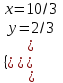; (10,3; 2/3).Отв. (4; 1); (10,3; 2/3).
IV. Метод почленного умножения (деления)
1)
; 
; 
; 
;
; 
; 
; 
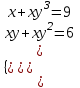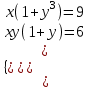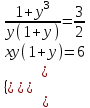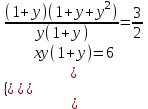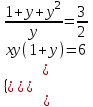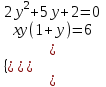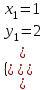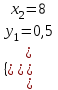; Отв. (1; 2); (8; 0,5).V. Метод однородных уравнений
Однородным уравнением с двумя неизвестными называется уравнение вида ax2 + bxy + cy2 = 0.
1)
; 
; 
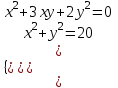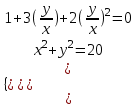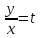
1 + 3t+ 2t2 = 0, 2t2 + 3t + 1 = 0, t = -1; -1/2
а)
t = -1,
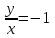, y = -x
, 
, 
, 
; (
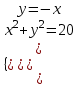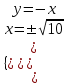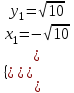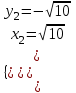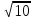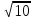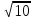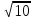,- ), (- , )б) t = -1/2,
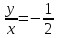, x=-2y
; 
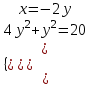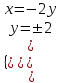; (2; -4), (-2; 4)Отв. (
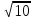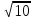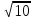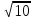,- ), (- , ),(2; -4), (-2; 4)VI. Симметрические системы
Симметрическая система – система, все уравнения которой симметрические. Симметрические уравнения от двух переменных – уравнения, которые не изменяются при замене х на у и у на х. Для таких уравнений используют замену x + y = u, xy = v.
1)
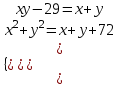; x + y = u, xy = v.
; 
; 
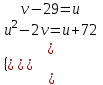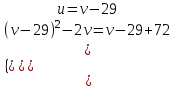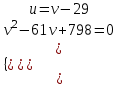
u1 = 13, v1 = 42, (u1, v1) = (13; 42)
u2 =-10, v2 = 19, (u2, v2) = (-10; 19)
а) (u1, v1) = (13; 42)
; 
; 
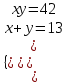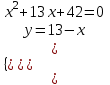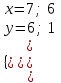; (7; 6), (6, 7)б) (u2, v2) = (-10; 19)
; 
; 
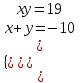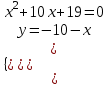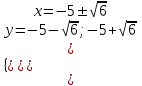
Отв. (7; 6), (6, 7), (-5+
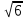; (-5 - 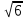), (-5 - 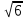; (-5 + 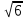)VII. Графический метод
1)
; 
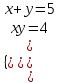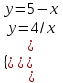
 y    5 4   1    5 4 1 x |
Системы иррациональных уравнений
1)
; 
; 
, 
; 
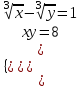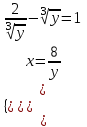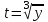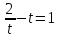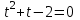, t =-2; 1а) t =-2
; 
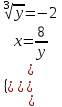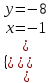; (-1;-8)б) t = 1
; 
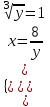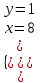
; (8; 1). Отв. (-1;-8), (8; 1).
2)
; 
; 
; 
; 
, 
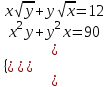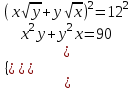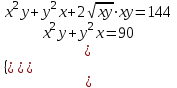
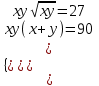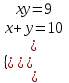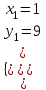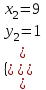; Отв. (1,9), (9, 1).3)
, 
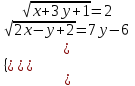
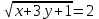= 4, x = 3 – 3y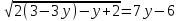
, 
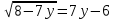
ОДЗ: 7у – 6 ≥ 0, у ≥ 6/7
8 – 7y = 49y2 – 84y + 36, 49y2 –77y + 28 = 0, 7y2 –11y + 4 = 0
D = 128 – 112 = 9, y= 4/7; 1
y= 4/7ОДЗ, у = 1, х = 0. Отв. (0; 1)
Уравнения с модулем
При решении уравнений и неравенств, содержащих модуль функции f(x), можно записать
|f(x)| =
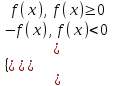
и решать уравнение и неравенство уже не содержащее знак модуля.
Рассмотрим некоторые виды уравнений с модулем и методы их решения.
I. Уравнение: |f(x)| = а (a ≥ 0)
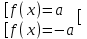, т.е. f(x) = а, либо f(x) = -а1) |x - 7| = 2 x – 7 = 2, либо x – 7 =- 2
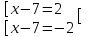; x = 9, 5. Отв. 9, 5 2) |x2 - 6| = 15 x2 - 6 = 15, либо x2 - 6 =- 15
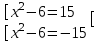; x2 = 21, x = 
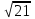; x2 = -9 < 0 – нет корнейОтв.
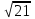
3) |x2 – 2х - 7| = 4 x2 - 2х - 7 = 4, либо x2 - 2х - 7 - 7 =- 4
; 
; 
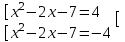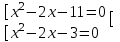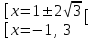
Отв. -1, 3; 1
