Коэффициент автокорреляции 2го порядка равен:


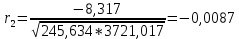
Коэффициент автокорреляции 3го порядка равен:


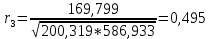
Коэффициент автокорреляции 4го порядка равен:


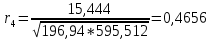
Таблица 8. - Результаты расчетов коэффициентов автокорреляции и коррелограмма .

Лаг (порядок) - L	Коэффициенты автокорреляции	Коррелограмма
1	0,3568	***
2	-0,0087	*
3	0,4952	******
4	0,4656	*****

Для выявления характера тенденции построим график ряда динамики с трендом.

---

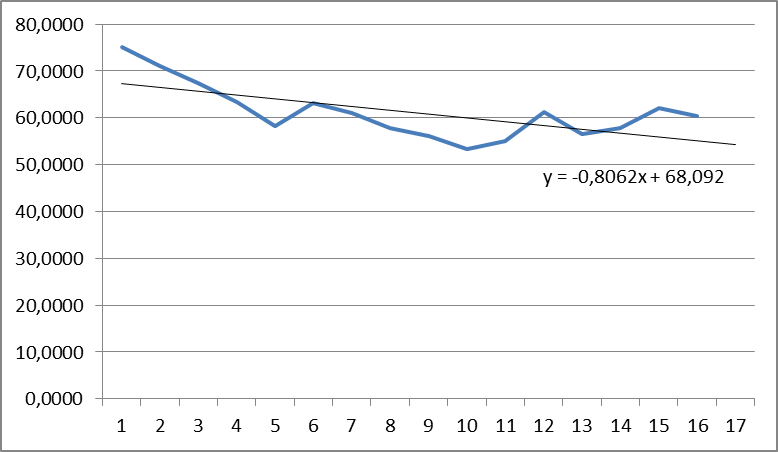
Рисунок 1. – Динамика курса доллара.
График данного временного ряда (рис. 1) свидетельствует о наличии еженедельных изменений курса доллара - снижения (период колебаний равен количеству недель). Поскольку амплитуда колебаний примерно постоянна, можно предположить существование аддитивной модели.

Рассчитаем цепные абсолютные приросты для определения модели. Полученные данные указывают на мультипликативную модель/

Проведем выравнивание исходных уровней ряда методом скользящей средней, полученные данные сведём в таблицу 9.
Таблица 9. - Расчет оценок сезонной компоненты в аддитивной модели

t	Tt	Итого за 4 недели	Скользящая средняя за 4 недели	Центрированная кользящая средняя	Оценка сезонной компоненты
1	2	3	4	5	6
1	71,0237
2	67,3843	261,0741	65,2685
3	63,7799	256,4533	64,1133	64,6909	0,9859
4	58,8862	250,7649	62,6912	63,4023	0,9288
5	66,4029	244,763	61,1908	61,9410	1,0720
6	61,6959	242,5869	60,6467	60,9187	1,0128
7	57,778	229,5074	57,3769	59,0118	0,9791
8	56,7101	221,5791	55,3948	56,3858	1,0058
9	53,3234	225,0675	56,2669	55,8308	0,9551
10	53,7676	226,1897	56,5474	56,4072	0,9532
11	61,2664	230,258	57,5645	57,0560	1,0738
12	57,8323	237,8005	59,4501	58,5073	0,9885
13	57,3917	236,9037	59,2259	59,3380	0,9672
14	61,3101	239,9707	59,9927	59,6093	1,0285
15	60,3696	243,9537	60,9884	60,4906	0,9980
16	60,8993

---

Полученные данные используем для расчета значений сезонной компоненты S (табл.10). Для этого найдем средние за каждую неделю оценки сезонной компоненты Si . В моделях с сезонной компонентой обычно предполагается, что сезонные воздействия за период взаимопогашаются. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем неделям должна быть равна нулю.

Таблица 10. - Расчет сезонной компоненты в мультипликативной модели

Показатели	Месяц	№ недели, i
		1	2	3	4
	1	-	-	0,9859	0,9288
	2	1,0720	1,0128	0,9791	1,0058
	3	0,9551	0,9532	1,0738	0,9885
	4	0,9672	1,0285	0,998	-
Итого за i-ую неделю каждого месяца		2,9943	2,9945	4,0368	2,9230
Средняя оценка сезонной компоненты для i-ой недели, 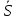t		0,9981	0,9882	1,0092	0,9743
Скорректированная сезонная компонента, St		1,0032	1,0032	1,0143	0,9793

Для данной модели имеем: 0,9981+0,9882+1,0092+0,9743=3,98 Определим корректирующий коэффициент: k = 4/3,98=1,005

Проверим условие равенства 4 суммы значений сезонной компоненты: 1,0032+1,0032+1,0143+0,9793 = 4
Определим компоненту T данной модели. Для этого проведем аналитическое выравнивание ряда с помощью линейного тренда (расчеты выполнены с помощью Ms Excel). Результаты аналитического выравнивания следующие:
T=-0,5312t+65,128

R-квадрат=0,9284
Подставляя в это уравнение значения t = 1, ..., 16, найдем уровни Τ для каждого момента времени (графа 5 табл.11). График уравнения тренда приведен на рисунке 2.

---

Таблица 11. - Расчет выровненных значений T и ошибок E в мультипликативной модели.

t	Yt	St	T*E	T	T*S	E= Yt/(T*S)	E²	(Yt-T*S)2
1	2	3	4	5	6	7	8	9
1	75,0890	1,0032	74,8515	66,9478	67,1602	1,1181	1,2501	62,8653
2	71,0237	1,0032	70,7950	66,2526	66,4666	1,0686	1,1418	20,7667
3	67,3843	1,0143	66,4328	65,5574	66,4964	1,0134	1,0269	0,7884
4	63,4445	0,9793	64,7873	64,8622	63,5178	0,9988	0,9977	0,0054
5	58,2087	1,0032	58,0246	64,1670	64,3706	0,9043	0,8177	37,9691
6	63,0975	1,0032	62,8943	63,4718	63,6769	0,9909	0,9819	0,3357
7	61,1094	1,0143	60,2465	62,7766	63,6757	0,9597	0,9210	6,5862
8	57,7780	0,9793	59,0009	62,0814	60,7946	0,9504	0,9032	9,1001
9	56,1727	1,0032	55,9950	61,3862	61,5810	0,9122	0,8321	29,2496
13	53,3641	1,0032	53,1922	58,6054	58,7947	0,9076	0,8238	29,4919
11	55,0858	1,0143	54,3079	59,9958	60,8551	0,9052	0,8194	33,2851
12	61,3045	0,9793	62,6020	59,3006	58,0715	1,0557	1,1144	10,4524
13	56,5616	1,0032	56,3827	58,6054	58,7914	0,9621	0,9256	4,9718
14	57,7821	1,0032	57,5960	57,9102	58,0973	0,9946	0,9892	0,0993
15	62,0506	1,0143	61,1744	57,2150	58,0345	1,0692	1,1432	16,1291
16	60,3696	0,9793	61,6474	56,5198	55,3483	1,0907	1,1897	25,2133
Итого	979,8261	16	979,9306	985,6552	985,732	15,901	15,8776	287,309

---

---

Смотрите также файлы

• Протокол от " " 2019 г. Е. И. Музычко Согласовано.docx

• Тест фио студента Фам Ван Фу Мань Ответы на тест.docx

• Рабочая программа внеурочной деятельности Робототехника (общеинтеллектуальное направление) 57 класс.docx

• Сптай орта мектебі кмм.docx

• Учет товаров и торговой наценки в предприятиях розничной торговли на примере ооо агроторг.docx