Файл: 2 оценить значимость полученных уравнений на уровне 0,05.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 195
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Построим график остатков
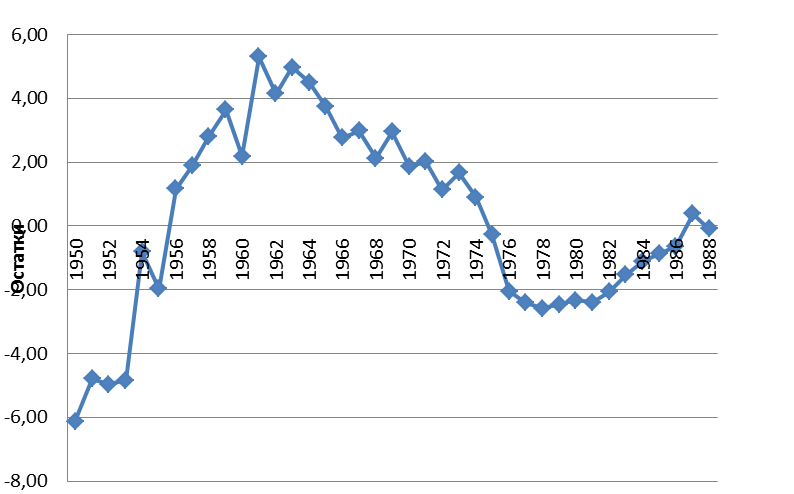
Рисунок 2. – График остатков
-
Видим, что значительные положительные остатки наблюдаются в период 1956-1976гг., когда численность населения сильно отклонялась от тренда в положительную сторону.
Задание 3.
Имеются условные данные о потребительских расходах на душу населения (тыс. руб.), средней заработной плате и других социальных выплатах по регионам РФ.
Выполнить дисперсионный анализ с помощью инструмента «Анализ данных» приложения MS Excel, составить уравнение регрессии, найти коэффициенты детерминации, корреляции, проверить целесообразность использования нелинейной регрессии (данные приведены в табл.3).
Таблица 3.
| Район | Потребительские расходы на душу населения | Средняя заработная плата и другие соц.выплаты |
| Y, тыс. руб. | X, тыс. руб. | |
| Уральский: | ||
| Респ.Башкортостан | 461 | 540 |
| Удмурская респ. | 784 | 809 |
| Курганская обл. | 298 | 540 |
| Оренбургская обл | 784 | 847 |
| Пермская обл. | 624 | 540 |
| Свердловская обл. | 784 | 1074 |
| Челябинск.обл. | 725 | 540 |
| Западно-Сибирский: | ||
| Респ.Алтай | 277 | 540 |
| Кемеровская обл. | 784 | 1251 |
| Новосибирская обл. | 573 | 540 |
| Омская обл. | 784 | 898 |
| Томская обл. | 784 | 540 |
| Тюменская обл. | 863 | 302 |
| Восточно - Сибирский: | ||
| Красноярский край | 784 | 654 |
| Иркутская обл. | 587 | 540 |
| Забайкальский край | 784 | 682 |
| Респ. Бурятия | 532 | 540 |
| Респ. Тыва | 784 | 780 |
| Респ. Якутия | 784 | 980 |
Решение:
| b | 0,3044 | 462,1628 | a | |
| Стандартная ошибка b | 0,163861 | 119,3164 | Стандартная ошибка а | |
| Коэффициент детерминации | 0,168743 | 163,1069 | Стандартная ошибка у | |
| F статистика | 3,450951 | 17 | Число степеней свободы | |
| Регрессионная сумма квадратов | 91808,66 | 452265,8 | Остаточная сумма квадратов | |
| Регрессионная статистика | ||||
| Множественный R | 0,410783 | |||
| R-квадрат | 0,168743 | |||
| Нормированный R-квадрат | 0,119845 | |||
| Стандартная ошибка | 163,1069 | |||
| Наблюдения | 19 | |||
| Дисперсионный анализ | |||||
| | df | SS | MS | F | Значимость F |
| Регрессия | 1 | 91808,66 | 91808,66 | 3,450951 | 0,080624 |
| Остаток | 17 | 452265,8 | 26603,87 | | |
| Итого | 18 | 544074,4 | | | |
Отчет:
| | Коэф-ты | Ст. ошибка | t-ст-ка | P-Знач. | Нижние 95% | Верхние 95% | Нижние 95,0% | Верхние 95,0% |
| Y-пересечение | 462,163 | 119,316 | 3,873 | 0,001 | 210,427 | 713,898 | 210,427 | 713,898 |
| Переменная X 1 | 0,304 | 0,164 | 1,858 | 0,081 | -0,041 | 0,650 | -0,041 | 0,650 |
Уравнение регрессии имеет вид:
y = 0,304x + 462,163
Очевидно, что при уменьшении x на единицу, y уменьшается на 0,304. В том случае, когда x = 0, у= 462,163.
В итоговых таблицах указано значение F-статистики Фишера: Fн=0,0732; а так же t-статистики Стьюдента: tн =3,873. Сравнивая эти значения с табличными, мы оцениваем качество уравнение регрессии и статистическую значимость коэффициентов регрессии. Например, t-табличное (для числа степеней 17), равно 2,13. Это значение меньше наблюдаемого, следовательно, коэффициенты регрессии статистически значимы; F табличное (с числом степеней свободы 1 и 17) равно 4,414; вычисленное значение F-статистики меньше табличного, соответственно, уравнение регрессии в целом незначимо.
Коэффициент детерминации R-квадрат равен 0,168. Это означает, что 16,8% исходных данных могут быть объяснены при помощи уравнения линейной регрессии.
Коэффициент корреляции R:
| R= | 1 | |
| -0,06548 | 1 |
Коэффициент корреляции между переменными x и y составляет -0,06548, то есть изменение одной величины приводит к противоположному изменению второй.
Задание 4.
По данным динамики валют выявить трендовую, периодическую и случайную составляющие ряда (T,S,E), оценить качество модели, сделать прогноз на ближайшие несколько недель (данные представлены в табл.4).
Таблица 4.- Исходные данные
| Валюта - доллар | ||
| Вариант | Недели | День недели |
| 17 | 17-33 | 7 |
Решение.
Согласно заданию, необходимо провести анализ курса доллара с 17 по 33 неделю года, день недели – воскресенье. Данные представлены в таблице 5.
Таблица 5. – Еженедельный курс доллара ЦБ РФ за период с 01.05.2022 года по 14.08.2022г, руб.
| Дата | 01.05 | 08.05 | 15.05 | 22.05 | 29.05 | 05.06 | 12.06 | 19.06 | 26.06 |
| Курс | 71,0237 | 71,0237 | 71,0237 | 71,0237 | 71,0237 | 71,0237 | 71,0237 | 71,0237 | 71,0237 |
| Дата | 03.07 | 10.07 | 17.07 | 24.07. | 31.07 | 07.08 | 14.08 | | |
| Курс | 53,7676 | 53,7676 | 53,7676 | 53,7676 | 53,7676 | 53,7676 | 53,7676 | | |
Определим коэффициент автокорреляции 1-го порядка, используя формулу линейного коэффициента корреляции:
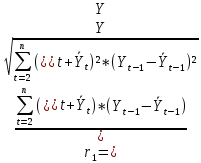
Таблица 6. – Промежуточные данные для расчёта коэффициента автокорреляции 1-го порядка
| t | Yt | Yt-1 | Yt - 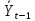 | Yt-1 - 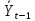 | (Yt- 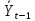 )² )² | (Yt-1 - 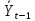 )² )² | (Yt- 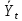 )* )*(Yt-1 - 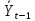 )² )² |
| 1 мая | 71,0237 | - | | | | | |
| 8 мая | 67,3843 | 71,0237 | 6,7705 | 14,2161 | 45,8392 | 202,0966 | 96,2494 |
| 15 мая | 63,7799 | 67,3843 | 3,1661 | 10,5767 | 10,0240 | 111,8659 | 33,4864 |
| 22 мая | 58,8862 | 63,7799 | -1,7276 | 6,9723 | 2,9847 | 48,6125 | -12,0456 |
| 29 мая | 66,4029 | 58,8862 | 5,7891 | 2,0786 | 33,5132 | 4,3204 | 12,0330 |
| 5 июня | 61,6959 | 66,4029 | 1,0821 | 9,5953 | 1,1709 | 92,0692 | 10,3827 |
| 12 июня | 57,778 | 61,6959 | -2,8358 | 4,8883 | 8,0420 | 23,8952 | -13,8623 |
| 19 июня | 56,7101 | 57,778 | -3,9037 | 0,9704 | 15,2392 | 0,9416 | -3,7881 |
| 26 июня | 53,3234 | 56,7101 | -7,2904 | -0,0975 | 53,1505 | 0,0095 | 0,7110 |
| 3 июля | 53,7676 | 53,3234 | -6,8462 | -3,4842 | 46,8710 | 12,1399 | 23,8539 |
| 10 июля | 61,2664 | 53,7676 | 0,6526 | -3,0400 | 0,4258 | 9,2418 | -1,9838 |
| 17 июля | 57,8323 | 61,2664 | -2,7815 | 4,4588 | 7,7370 | 19,8806 | -12,4022 |
| 24 июля | 57,3917 | 57,8323 | -3,2221 | 1,0247 | 10,3822 | 1,0499 | -3,3016 |
| 31 июля | 61,3101 | 57,3917 | 0,6963 | 0,5841 | 0,4848 | 0,3411 | 0,4067 |
| 7 августа | 60,3696 | 61,3101 | -0,2442 | 4,5025 | 0,0597 | 20,2722 | -1,0997 |
| 14 августа | 60,8993 | 60,3696 | 0,2855 | 3,5620 | 0,0815 | 12,6876 | 1,0168 |
| Сумма | 969,8214 | 908,9221 | - | - | 236,0054 | 559,4242 | 129,6565 |
| Среднее значение | 60,6138 | 56,80763 | - | - | - | - | - |
Далее рассчитаем коэффициент автокорреляции 2го порядка по формуле:
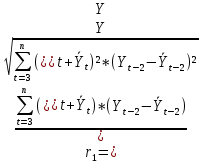
Промежуточные значения для расчета сведём в таблицу 7.
Таблица 7 – Промежуточные значения для расчета коэффициента автокорреляции 2го порядка.
| t | Yt | Yt-2 | Yt - 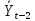 | Yt-2 - 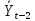 | (Yt- 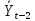 )² )² | (Yt-2 - 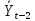 )² )² | (Yt-  )* )*(Yt-2 - 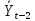 )² )² |
| 1 мая | 71,0237 | - | - | - | - | - | - |
| 8 мая | 67,3843 | - | - | - | - | - | - |
| 15 мая | 63,7799 | 71,0237 | 6,7316 | 14,4535 | 45,3142 | 208,9046 | 97,2951 |
| 22 мая | 58,8862 | 67,3843 | 1,8379 | 10,8141 | 3,3778 | 116,9455 | 19,8751 |
| 29 мая | 66,4029 | 63,7799 | 9,3546 | 2,3160 | 87,5082 | 5,3640 | 21,6655 |
| 5 июня | 61,6959 | 58,8862 | 4,6476 | 9,8327 | 21,6000 | 96,6826 | 45,6984 |
| 12 июня | 57,778 | 66,4029 | 0,7297 | 5,1257 | 0,5324 | 26,2731 | 3,7402 |
| 19 июня | 56,7101 | 61,6959 | -0,3382 | 1,2078 | 0,1144 | 1,4589 | -0,4085 |
| 26 июня | 53,3234 | 57,778 | -3,7249 | 0,1399 | 13,8750 | 0,0196 | -0,5212 |
| 3 июля | 53,7676 | 56,7101 | -3,2807 | -3,2468 | 10,7631 | 10,5415 | 10,6517 |
| 10 июля | 61,2664 | 53,3234 | 4,2181 | -2,8026 | 17,7922 | 7,8544 | -11,8215 |
| 17 июля | 57,8323 | 53,7676 | 0,7840 | 4,6962 | 0,6146 | 22,0546 | 3,6818 |
| 24 июля | 57,3917 | 61,2664 | 0,3434 | 1,2621 | 0,1179 | 1,5930 | 0,4334 |
| 31 июля | 61,3101 | 57,8323 | 4,2618 | 0,8215 | 18,1628 | 0,6749 | 3,5012 |
| 7 августа | 60,3696 | 57,3917 | 3,3213 | 4,7399 | 11,0309 | 22,4670 | 15,7427 |
| 14 августа | 60,8993 | 61,3101 | 3,8510 | -56,5702 | 14,8301 | 3200,1838 | -217,8507 |
| Сумма | 969,821 | 848,553 | - | - | 245,634 | 3721,017 | -8,317 |
| Ср.значение | 57,048 | 56,570 | - | - | - | - | - |