Файл: Лабораторная работа ms excel Ввод и форматирование данных Цель работы отработка базовых навыков работы в ms.doc

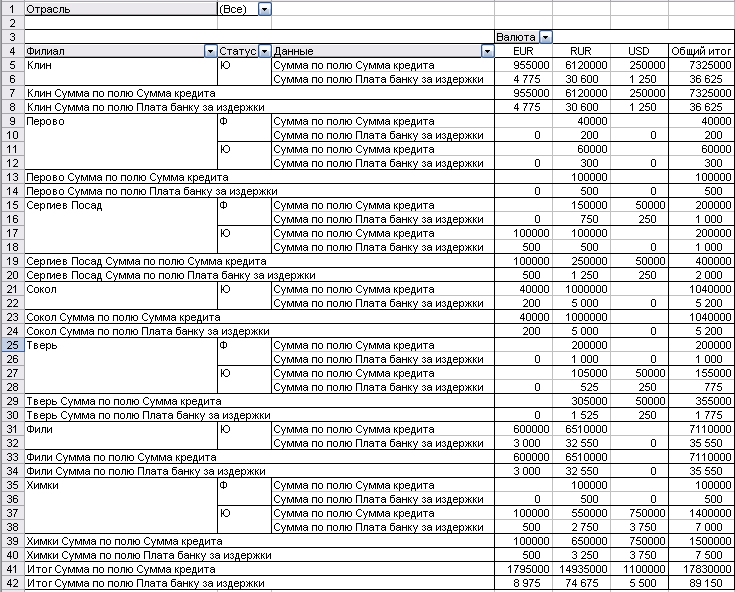
Рис. 14. Фрагмент сводной таблицы с вычисляемым полем

Сформируйте вычисляемый элемент, отобража­ющий сумму кредита по Московскому региону.

Выполните следующие действия:

1. 
   Поместите курсор на то поле, которое будет содержать новый вычисляемый элемент. В нашем примере таким полем будет поле Филиал.
   
2. 
   На панели инструментов Сводные таблицы раскройте список кнопки Сводная таблица и выберите команды: Формулы → Вычисляемый объект...
   

В результате появится диалоговое окно Вставка вычисляемого элемента (рис. 15).



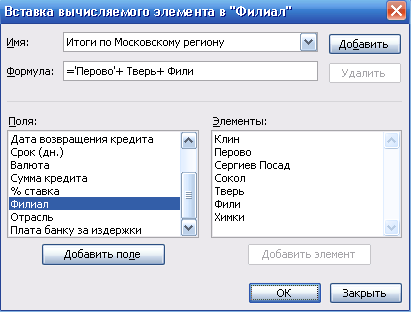
Рис. 15. Окно формирования формулы вычисляемого элемента сводной таблицы

3. 
   В поле Имя укажите название нового элемента, в поле Фор­мула введите формулу расчета нового элемента. В нашем при­мере имя нового объекта — Итоги по Московскому региону, а формула имеет следующий вид: ='Перово'+Сокол+Фили.
   
4. 
   Для добавления созданного нового элемента в поле сводной таблицы щелкните по кнопке Добавить.
   
5. 
   Для закрытия диалогового окна щелкните по кнопке ОК.
   

Иногда требуется сгруппировать данные в соответствии с определен­ным временным интервалом. Например, на основании базы данных (рис. 1) необходимо проанализировать выдачу кредитов по меся­цам (кварталам).

• 
  Для этого первоначально создайте сводную таблицу на отдельном листе, в которой согласно макету (рис. 10) в области строк приведены даты выдачи кредитов, в области столбцов, например, филиалы, в кото­рых выданы кредиты, в области данных – суммы кредитов.
  

Результат выполненных действий должен быть, как на рис. 16.



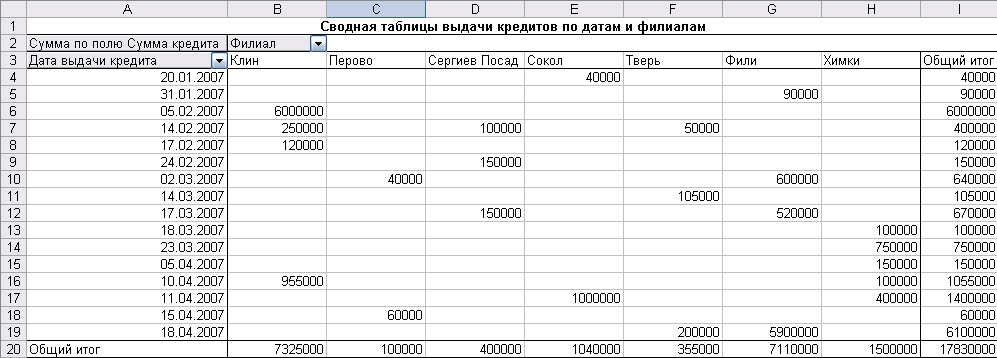
Рис. 16. Сводная таблица выдачи кредитов в филиалах по датам

Далее для создания группы по месяцам (кварталам) необходимо выпол­нить следующие операции:

1 ПКМ по ячейке в пределах столбца Дата выдачи кредита → Команда Группа и структура → Группировать...

---

¹ → Задать интервал группировки → С шагом: Месяцы (Кварталы, Годы,...) → ОК

¹ Последующие операции выполняются в окне, представленном на рис. 17.



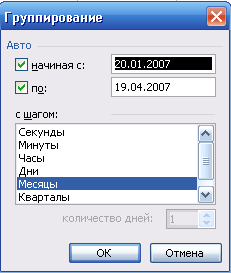
Рис. 17. Окно задания параметров группировки сводной таблицы

В результате будет сформирована сводная таблица с группировкой дан­ных по месяцам (рис. 18).



Рис. 18. Сгруппированная сводная таблица выдачи кредитов в филиалах по месяцам

• 
  Разгруппируйте сводную таблицу (исполь­зуя контекстное меню) и выполните новую группировку по кварталам.
  

Завершив формирование сводной таблицы, представьте ее более красочно, в виде одного из 22 вариантов оформления – 10 отчетов, 10 таблиц, классической сводной таблицы и макета без форматирова­ния (рис. 18). Установите курсор в пределах сводной таблицы → Кнопка Формат отчета панели Сводные таблицы → Выбрать макет отчета → Кнопка ОК.



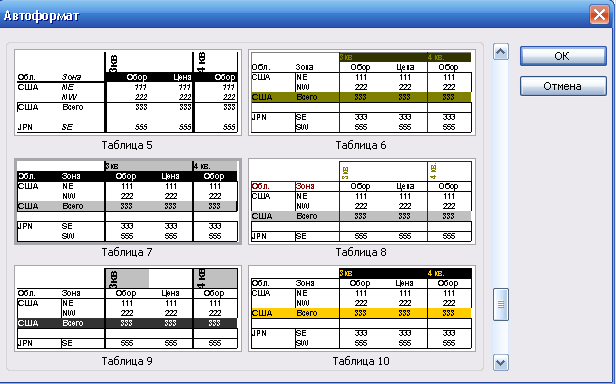
Рис. 18. Окно Автоформатирования сводной таблицы

Задание 5. Консолидация данных

Другим инструментом обобщения и анализа данных является консоли­дация.

Например, если нужно обобщить данные (просуммировать, под­считать общее количество, найти среднее, максимум, минимум и др.) из одной и той же ячейки на разных листах рабочей книги или на раз­ных книгах, из нескольких однотипных таблиц на одном и том же или нескольких листах книги либо нескольких книг, следует консолиди­ровать эти ячейки, и тогда заданная операция будет выполняться авто­матически.

Таким образом, консолидация данных позволяет собрать в одной области информацию из нескольких источников данных.

Консолидировать данные можно несколькими способами:

• 
  по расположению данных;
  
• 
  по категориям;
  
• 
  с помощью трехмерных ссылок в формулах.
  

Метод консолидации по расположению данных используется, если дан­ные занимают одинаковое число ячеек с одинаковым расположением в нескольких местах одной рабочей книги.

Метод консолидации по категориям

---

(или по подписям) используется, если требуется обобщить данные таблиц, расположенных на разных листах рабочей книги, имеющих одинаковые заголовки столбцов и рядов, но различные макеты диапазонов данных.

Метод трехмерных формул позволяет объединить ячейки с помощью формул, используя в них ссылки на ячейки, расположенные в разных листах рабочей книги или в разных книгах.

Рассмотрим реализацию метода консолидации.

Пусть обобщенные данные необходимо расположить на отдельном листе рабочей книги. Тогда для выполнения, например, консолидированного суммирования числовых данных необходимо выполнить следующие операции.

1. 
   Создайте таблицы одинаковой структуры посещаемости стран за январь (на новом листе) и за февраль (на новом листе) (см. рис. 1).
   

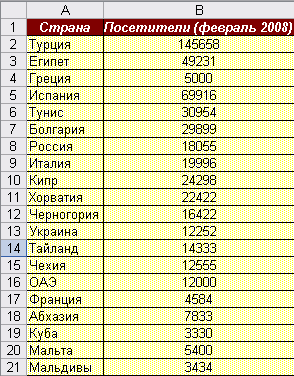
Рис. 1 Таблица посещаемости стран за февраль

2. 
   Выделите на новом листе одну или несколько ячеек.
   
3. 
   Используя оконное меню, выберите команды: Данные → Кон­солидация. В результате на экране появится диалоговое окно Консолидация (рис. 2).
   
4. 
   В диалоговом окне в поле Функция выберите функцию для обобщения данных (в нашем примере, функцию Сумма).
   
5. 
   В поле Ссылка укажите первый диапазон ячеек, кото­рый будет участвовать в консолидации. Его не следует вводить непосредственно, требуемый диапазон необходимо выделять.
   
6. 
   Для включения диапазона в группу обрабатываемых данных нажмите Добавить. Выбранный диапазон отобра­зится в поле Список диапазонов.
   
7. 
   Повторите ввод других диапазонов данных, участвующих в обобщении, используя поле Ссылка и кнопку Добавить.
   
8. 
   В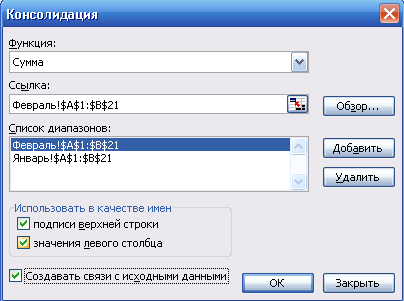 зависимости от выбранного способа консолидации устано­вить требуемые значения группы флажков Использовать в качестве имен. Если консолидация выполняется по рас­положению данных, то флажки не устанавливаются. Если кон­солидация выполняется по категориям, то устанавливаются флажки, соответствующие подписи верхней строки и значению первого столбца. Для создания связи между источником дан­ных и обобщенными данными установите флажок Создавать связи с исходными данными.
   
9. 
   Закройте диалоговое окно кнопкой ОК, что приведет к объеди­нению данных в одну или несколько изначально выделенных ячеек. Консолидация будет завершена.
   

---

Рис. 2. Диалоговое окно консолидации данных



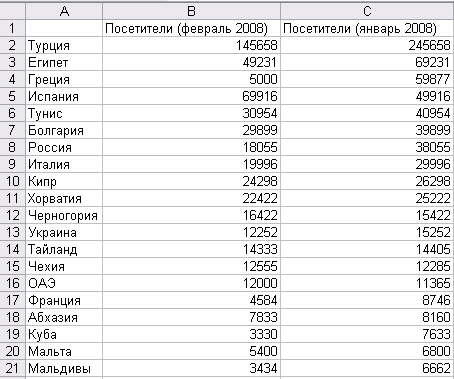
Рис. 3. Результат консолидации данных

Лабораторная работа № 7. Поиск решения, Подбор параметра

Подбор параметра

Когда желаемый результат одиночной формулы известен, но неизвестны значения, которые требуется ввести для получения этого результата, можно воспользоваться средством Подбор параметра.

При подборе параметра MS Excel изменяет значение в одной ячейке до тех пор, пока формула, зависимая от этой ячейки, не возвращает нужный результат.

Этот инструмент удобен, если нам нужно знать, на сколько изменить одну входную величину, чтобы получить желаемый результат.

Поиск решения

Поиск решения является инструментом оптимизации, с его помощью можно найти оптимальное или заданное значение некоторой ячейки путем подбора значений нескольких ячеек, удовлетворяющих нескольким граничным условиям.

Программа Поиск решения относится к надстройкам (это компоненты, установка которых позволяет дополнить Excel новыми командами и функциями) и может отсутствовать в меню. Для ее установки выполните команду Сервис→ Надстройки.... Откроется диалоговое окно, в котором установите галочку для надстройки Поиск решения и нажмите ОК. Если процесс установки завершается успешно, то в меню Сервис появляется ещё один пункт – Поиск решения.

Чтобы запустить инструмент Поиск решения выполните Сервис → Поиск решения. При этом появится диалоговое окно с установкой параметров поиска.

Ц 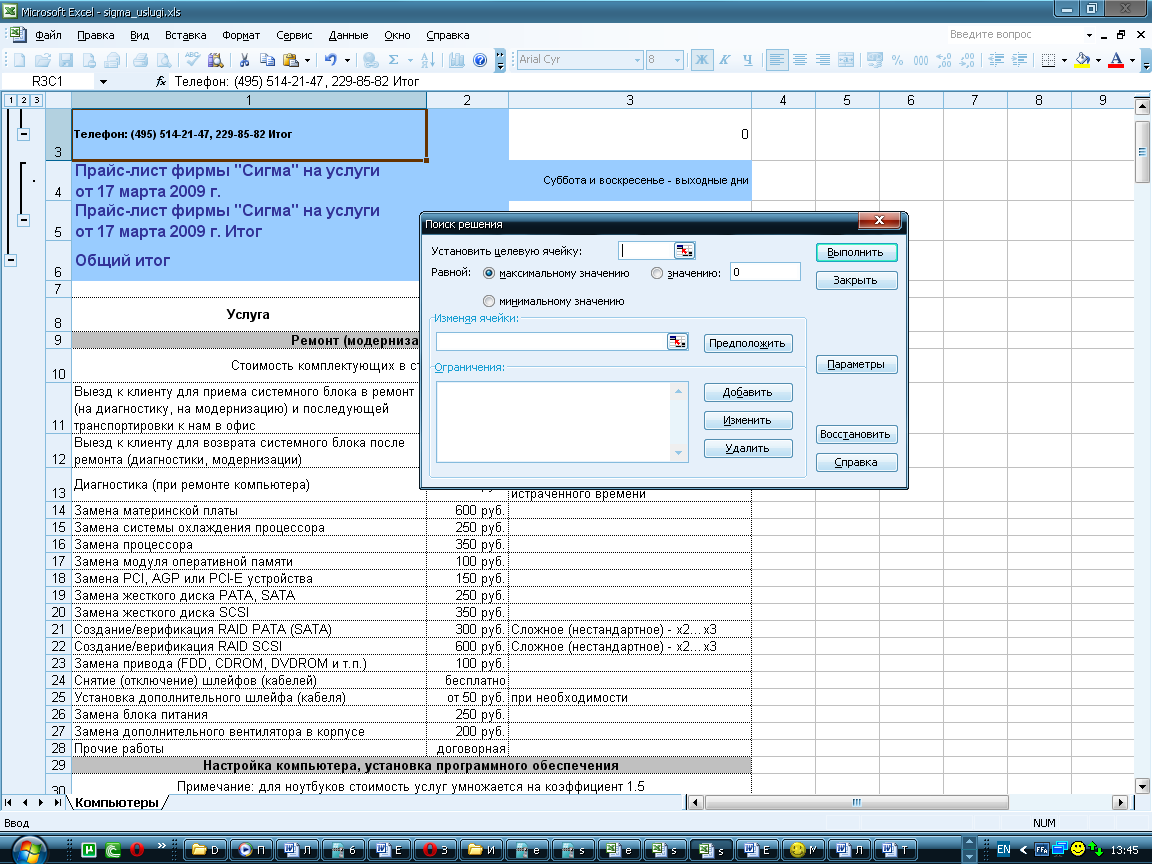елевая ячейка – та, для которой нужно найти максимальное, минимальное или заданное значения. Она должна содержать формулу, зависящую от изменяемых ячеек (прямо или косвенно). Пока не будет найдено решение, программа подбирает значения изменяемых ячеек.

Изменяемые ячейки – те, от которых зависит значение целевой ячейки.

Существует возможность определения результирующего значения при необходимости изменения нескольких используемых в формуле ячеек, для которых существуют несколько ограничений.

---

Кнопка Выполнить инициирует процесс решения. Через некоторое время в диалоговом окне появится сообщение о том, найдено решение или нет.

Цель работы: Знакомство с методами решения задач оптимизации в электронных таблицах.

Одной из задач оптимизации является задача об использовании сырья. При этом решается задача оптимизации целевой функции – критерия задачи при заданных в виде равенств и неравенств ограничений. Принятие оптимальных решений требует выполнения трех этапов:

1. анализ исходных данных;

2. создание математической модели;

3. решение задачи на компьютере;

4. анализ полученных результатов.

Рассмотрим простейшую задачу, в которой проиллюстрируем некоторые понятия задач оптимизации. Отметим, что рассматриваемая задача относится к задачам нелинейного программирования.

Задача № 1. Расчет изделия с минимальным расходом материала

Спроектировать бак, имеющий форму прямоугольного параллелепипеда, объем которого равен V = a·b·h, где a, b, h –стороны бака (длина, ширина, высота). Требуется определить размеры бака объемом V = 2000, чтобы на его изготовление пошло как можно меньше материала. Площадь материала для изготовления бака равна сумме площадей всех стенок бака и выражается формулой: S = a·b + a·b + b·h + b·h + a·h + a·h = 2(a·b + (a +b)h).



Составим математическую модель.

Очевидно, что целью задачи является экономия материала. Тогда целевая функция F зависящая от трех переменных a, b и h – это просто площадь необходимого материала S.

Необходимо найти при каких значениях a, b и h целевая функция F будет минимальной.

Итак, задача может быть записана в форме математической модели:

F = S → min

V = 2000.

Эта запись читается так:

минимизировать величину S при условии, что V = 2000. Подставив значения F и S, получим: F=2·(a·

---