Файл: Лабораторная работа ms excel Ввод и форматирование данных Цель работы отработка базовых навыков работы в ms.doc

b + (a + b)·h) → min, а т.к. V=a·b·h, то a·b·h = 2000

И, наконец, нужно добавить ограничения (граничные условия) на параметры бака: а > 0, b > 0, h > 0.

Составим таблицу для решения задачи и решим ее средствами Excel.

♠ Будьте внимательны: имена столбцов набираются латинскими буквами!

Ввод данных

Введите текст:	в ячейку А1 – Целевая функция F;
	в ячейку А3 – Расчетные показатели;
	в ячейки А4:А7 – a=, b=, h=, V=.

---

Ячейки D1, D2, D3 будем использовать для ввода начальных значений переменных a, b и h, для дальнейшего поиска оптимального решения. Пока будем считать их равными нулю.

В ячейку B1 введем для целевой функции F формулу, которая будет иметь следующий вид =2*(D1*D2+(D1+D2)*D3)

В ячейки B4, B5 и B6 последовательно введем формулу со ссылкой на ячейки D1, D2, D3 (в B4 =D1, в B5 =D2 и в B6 =D3), для дальнейшего ввода ограничений на параметры бака.

В ячейку B7 введите формулу =D1*D2*D3 для расчета объема бака, т.е. ограничения по объему, который должен быть равен 2000.

Приступим к поиску решения задачи.

Выберите команду Сервис–Поиск решения. Появится окно диалога «Поиск решения» – рис. 1.



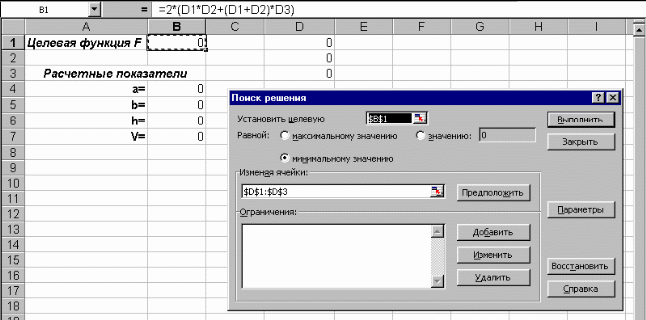
Рис. 1 Окно диалога «Поиск решения». Указатель находится в ячейке В1.

Так как формула для целевой функции находится в ячейке B1, то нужно щелкнуть мышью на этой ячейке. В поле окна диалога «Установить целевую ячейку» появится автоматически абсолютная ссылка $B$1. (Примечание: можно набрать значение абсолютной ссылки с клавиатуры, но щелкнуть мышью проще!).

В поле «Изменяя ячейки» укажите ссылку на диапазон ячеек D1:D3.

Установите переключатель «Минимальное значение».

Теперь необходимо ввести ограничение для поиска решения. Нажмите кнопку Добавить, чтобы ввести информацию в поле Ограничения – рис. 2.



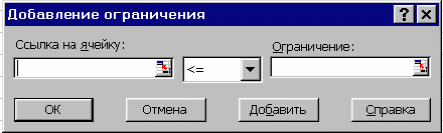
Рис. 2 Окно диалога «Добавить ограничения»

В поле Ссылка на ячейку введите B4. В списке неравенств выберите >= – больше или равно. В поле Ограничение введите число 0.

Нажмите кнопку Добавить.

Введите аналогичные ограничения для ячеек B5 и B6. Введите ограничение для ячейки B7: =2000. После ввода последнего ограничения нажмите клавишу Enter или кнопку OK.

Окно диалога «Поиск решения» примет следующий вид – рис. 3.

---

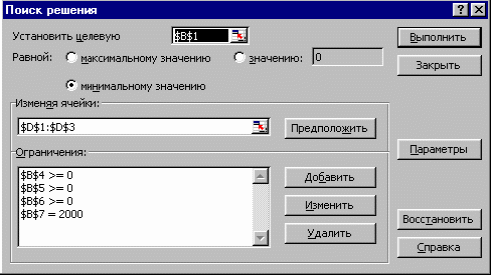
Рис. 3 Окно диалога «Поиск решения» после ввода ограничений

Решение задачи

Теперь все параметры для поиска решения введены и, можно дать команду к выполнению поиска решения. Нажмите кнопку Выполнить. В окне Результаты поиска решения выведено сообщение «Поиск не может найти подходящего решения», т.к. в ячейках D1, D2, D3 были заданы нулевые начальные значения (рис. 4).



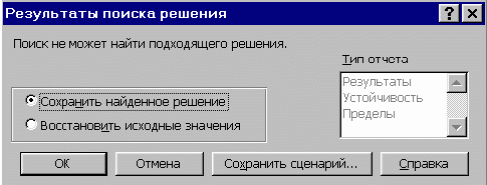
Рис. 4 Окно Результаты поиска решения (при нулевых начальных данных!)

При решении задач линейного программирования достаточно часто не удается получить оптимального решения. Это происходит по следующим причинам:

• Неправильная математическая модель или неправильные исходные данные.

• Неограниченность целевой функции. При максимизации целевая функция должна быть

ограничена сверху, при минимизации – снизу.

Измените начальные условия в ячейках D1:D3 на 1. Снова выберите команду Сервис – Поиск решения и нажмите кнопку Выполнить. Теперь в окне поиска решения появилось сообщение: «Решение найдено. Все ограничения и условия оптимальности выполнены». (Примечание: если в эти ячейки ввести отрицательные числа, то согласно заданным ограничениям, решение все равно будет найдено).



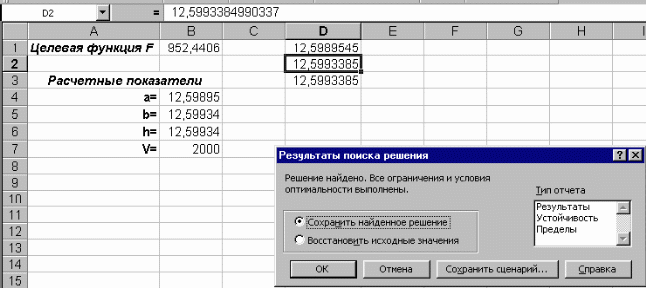
Рис. 5 Окно Результаты поиска решения (при ненулевых начальных данных!)

Чтобы получить отчет по найденному решению в окне Результаты поиска решения выберите Тип отчета: Результаты, нажав кнопку OK, получите лист с отчетом по результатам поиска решения. Перед тем листом, где записана постановка задачи автоматически будет вставлен лист Отчет по результатам 1. В этом отчете содержится ответ на поставленную задачу.

---

Искомый параллелепипед оказался кубом со сторонами ≈ 12,6.

Переименуйте рабочий лист и дайте ему название Бак.

Задача № 2. План выгодного производства

Условие задачи: Предположим, что мы решили производить несколько видов конфет. Назовем их условно "A", "B" и "C".

Конфеты можно производить в любых количествах (сбыт обеспечен), но запасы сырья ограничены.

Известно, что реализация 10-ти килограмм конфет "А" дает прибыль 9 р., "В" – 10 р. и "С" – 16 р.

Надо определить, каких конфет и сколько десятков килограмм необходимо произвести, чтобы общая прибыль от реализации была максимальной.

Решение задачи: Перейдем на другой лист рабочей книги, переименуйте его Конфеты, создайте таблицу с данными норм расхода сырья как показано на рис. 6. (ячейки B6, C6, D6 имеют формат Денежный).



Рис. 6. Таблица с данными норм расхода сырья.

Создайте и введите формулы в таблицы для нахождения решения поставленной задачи, как указано на рис 7.

Примечание: Количество конфет будет измеряться в десятках килограмм, т.к. нормы расхода сырья и получаемая от этого прибыль тоже приведены из расчета на 10 кг конфет.



Рис. 7. Таблицы с формулами для Поиска решения максимальной прибыли

Обратите внимание, что в ячейках А17, В17, С17 находится формула, отражающая сумму расхода сырья на производство каждого вида конфет, при этом каждая из них имеет ограничение по количеству имеющегося сырья. В меню Сервис активизируйте команду Поиск решения и опишите его ограничения, как показано на рис 8.



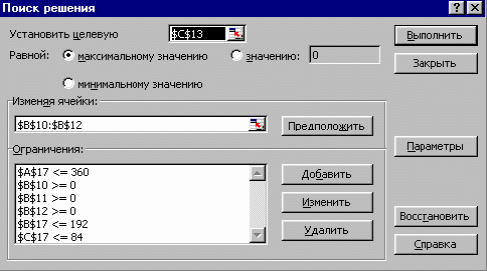
Рис. 8. Вид окна Поиск решения с заданными ограничениями.

Если Вы сделали все верно, то решение будет таким, как на рис 9.

---

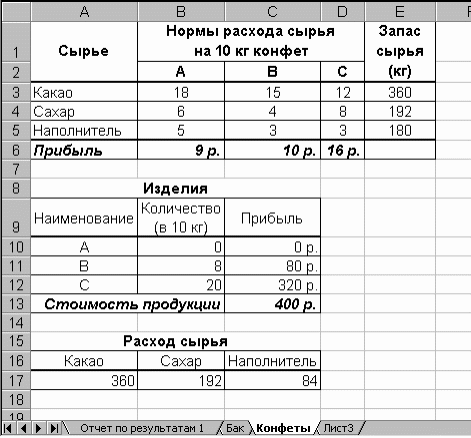
Рис. 9. Вид рабочего листа "Конфеты" после нахождения решения

Вывод: Из решения видно, что оптимальный план выпуска предусматривает изготовление 80 кг конфет "В" и 200 кг конфет "С". Конфеты "А" производить не стоит. Полученная Вами прибыль составит 400 р. При этом сырье израсходуется полностью, кроме наполнителя, расход которого составит 84 кг из имевшихся 180 кг.

Задача № 3. Транспортная задача

В пунктах A и B находятся соответственно 150 и 190 т горючего. Пунктам 1, 2, 3 требуются соответственно 160, 70, 110 т. горючего. Стоимость перевозки 1 т горючего из пункта A в пункты 1, 2, 3 равна 60, 10, 40 тыс. руб. за 1 т соответственно, а из пункта B в пункты 1, 2, 3 – 120, 20, 80 тыс. руб. за 1 т соответственно. Составьте план перевозок горючего, минимизирующий общую сумму транспортных расходов.

Технология работы:

1. 
   Исходные данные задачи представлены в табл. 1.
   

Таблица 1

Исходные данные

Поставщики	Потребители			Запасы
	1	2	3
A	60	10	40	150
B	120	20	80	190
Потребность	160	70	110

---