Файл: Лабораторная работа 1. Определение земного ускорения свободного падения при помощи оборот ного и математического маятников.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 213
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
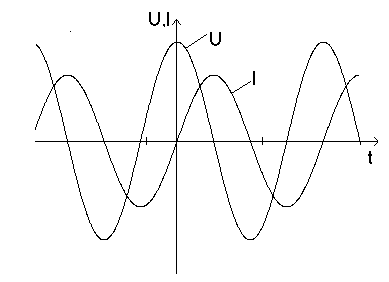
Рис. 8
Индуктивность контура равна связанному с ним магнитному потоку, если в контуре идет ток, равный единице (L= Ф/I). Единицей индуктивности в системе СИ служит Генри (1 Гн= 1 Вб/А). Индуктивность зависит от формы и размеров контура и от магнитной проницаемости среды.
Сдвиг фаз обусловлен тормозящим действием электродвижущей силы самоиндукции: она препятствует как нарастанию, так и убыванию тока в цепи, поэтому максимум тока наступает позднее, чем максимум напряжения. Наличие омического сопротивления привело бы к уменьшению сдвига фаз. Из (7) следует, что амплитуда напряжения равна U0= I0 L и, следовательно, величина ZL=wL играет ту же роль, что и сопротивление участка. Она представляет собой индуктивное сопротивление катушки.
Оно пропорционально круговой частоте тока и величине индуктивности. Эта зависимость объясняется тем, что индуктивное сопротивление обусловлено действием электродвижущей силы самоиндукции, уменьшающей эффективный ток и, следовательно, увеличивающей сопротивление. Величина же этой э.д.с. ( следовательно, сопротивления) пропорциональна индуктивности катушки L и скорости изменения тока, т.е. круговой частоте .
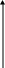
 U0=I0 L
U0=I0 L/2
О I
Рис. 9
Полученные результаты представим на векторной диаграмме (рис.9). Вектор, изображающий колебания напряжения, повернут относительно оси токов в положительном направлении (против часовой стрелки) на угол /2, а его длина равная амплитуде есть I0 L.
4. Закон Ома для переменных токов.
Пользуясь результатами, полученными в п.п. 1-3, можно найти соотношение между колебаниями тока и напряжения в любой цепи.
Рассмотрим последовательное соединение сопротивления, емкости и индуктивности (рис.10). Ток в цепи изменяется по закону синуса I= I0 sin wt .
Вычислим напряжение между концами участка цепи. Так как при последовательном соединении проводников складываются напряжения, то искомое напряжение и есть сумма трех напряжений: на сопротивлении, емкости и индуктивности, причем каждое изменяется по закону синуса.



 а А R
а А R 





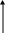



 C
C 

 U V I
U V I 


б L
Рис. 10
Для сложения этих трех гармонических колебаний воспользуемся векторной диаграммой напряжений. Колебания напряжения на сопротивлении изображаются на ней вектором Uа, направленном вдоль оси токов, колебания же напряжения на индуктивности и емкости – векторами, перпендикулярными к оси токов, с длинами I0 L и I0/ C.
Складывая два последних колебания, получим одно, изображаемое вектором Uр, перпендикулярным к оси токов и имеющим длину
Up= I0 (L- 1/C).
Полное напряжение можно рассматривать как сумму двух гармонических колебаний: напряжения Ua (активная составляющая напряжения), совпадающего по фазе с током, и напряжения Uр (реактивная составляющая напряжения), отличающегося по фазе на /2 (рис.11).
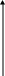 I0 L
I0 L 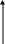

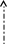

U0
Up=I0(L – 1/C)
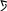
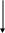

 О I
О IUa=I0 R
I0/C
Рис. 11.
Оба эти колебания, складываясь, дают гармоническое колебание
U= U0 sin (t+), (8)
которое изображается векторной суммой векторов Uа и Up, причем длина результирующего вектора равна амплитуде напряжений U0, а угол, образованный результирующим вектором с осью токов, - сдвигу фазы между током и напряжением .
Из треугольника напряжений получаем:
U0= I0 R2+(L – 1/C)2 (9)
Из рис.11 следует tg = (L – 1/C
)/ R (10)
Полное сопротивление в цепи переменного тока
(11)
Активное сопротивление участка цепи
R = Z cos (12)
Реактивное сопротивление цепи
= Z sin = L – 1/C (13)
Наличие реактивного сопротивления не сопровождается выделением тепла. Соотношения (10,11,12,13) можно получить из прямоугольного треугольника, который называется треуголником сопротивлений (рис. 12).


Полное
сопротивление Z Реактивное
сопротивление

Активное
сопротивление R
Рис. 12
В таблице 1 приведены полное сопротивление и фазовый сдвиг для цепей с различными комбинациями активного сопротивления R (Oм), индуктивности L (Гн), емкости С (Ф). Самым общим случаем в таблице является случай 6. Все остальные получаются из него как частные.
Таблица 1.
| № п/п | Схема цепи | Вклю-чены | Полное сопротивление | Фазовый сдвиг | Примечание |
| 1. 2. 3. 4. 5. 6. | | R(Ом) L (Гн) C (Ф) R (Oм) С (Ф) R(Ом) L(Гн) R(Ом) L(Гн) С(Ф) | Z = R ZL= L ZC = 1/C Z = R2 +(1/C)2 Z=R2 + (L)2 Z= R2 +(L-1/C)2 | = 0 = /2 = - /2 tg = tg = L/R tg=(L – 1/C)/ R | Ток по фазе совпадает с напряжением Напряжение опережает ток на Т/4 Напряжение отстает от тока на Т/4 Напряжение отстает от тока Напряжение опережает ток Напряжение отстает или опережает ток в зависимости от преобладания емкостного (1/C) или индуктивного (L) cопротивлений. |
Порядок выполнения задания.
1. Собрать схему с сопротивлением R (рис.1). Переключатели пределов шкалы вольтметра и амперметра установить на максимальные значения.
2. Включить схему в электрическую сеть переменного тока. При этом нужно следить, чтобы стрелки приборов не вышли за пределы шкалы. Если стрелка приборов отклоняется слабо, меньше половины шкалы, переключить прибор на меньший предел измерений.
3. Отсчитать показания по шкале вольтметра и амперметра nv и na (количество делений) и вычислить значения напряжения и тока:
U = Uпр.*nv/nш и I = Iпр.*na/nш
где Uпр.= 30V, Iпр.= 10A, 20A, 40A - предельные значения шкалы приборов, nш – полное число делений шкалы.
4. Определить значение R по измеренным значениям напряжения U и силы тока I. Данные занести в таблицу.
5. Включить в цепь вместо сопротивления конденсатор (рис.4) и выполнить измерения в том же порядке. Рассчитать сопротивление емкости Zc и определить емкость конденсатора С. Данные занести в таблицу.
6. Собрать схему с катушкой индуктивности L (рис.7). Омическое сопротивление (активное сопротивление) катушки равно RL=13 Ом.
7. Измерить напряжение и силу тока в цепи и произвести расчет полного сопротивления Z, индуктивного сопротивления ZL и индуктивности L. Данные занести в таблицу.
8. Собрать схему с активным сопротивлением R, индуктивностью L и емкостью С ( рис.10). Включить ее в цепь и по показаниям приборов определить полное сопротивление цепи. Данные занести в таблицу.
9. Рассчитать полное сопротивление цепи по формуле (11). Значения R, L, C взять из предыдущих упражнений.
10. Сопоставить измеренное (Zизм.) и вычисленное (Zвыч.) полное сопротивление.
Контрольные вопросы.
-
Какой физический смысл омического и реактивного сопротивлений в цепи переменного тока? -
Какие физические величины измеряют амперметр и вольтметр в цепи переменного тока? -
От чего зависят сопротивления катушки индуктивности и конденсатора в цепи переменного тока? -
Написать закон Ома для переменного тока. -
Начертить схемы включения приборов при измерении сопротивления, емкости и индуктивности.