Файл: Лабораторная работа 1. Определение земного ускорения свободного падения при помощи оборот ного и математического маятников.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 204
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
0 (предельным) угол преломления достигает 900 , то есть преломлённый луч скользит по границе раздела двух сред (рис.2). Данное явление получило название полного отражения. При всех углах 0 свет преломляться не будет.



 n1 0 10
n1 0 10
n2
Рис. 2.
Для полного отражения фомула (2) будет иметь вид
Sin 0 = n 12 = n 2 / n 1 , n 2 < n 1. (3)
В явлениях преломления и отражения света проявляется взаимодействие света с веществом, в результате чего происходит изменение скорости света. С этой точки зрения , относительный показатель преломления характеризует степень изменения скорости света при переходе его из среды 1 в среду 2, то есть n 12 = v 1 / v 2 (4)
Cоотношение (4) выражает физический смысл относительного показателя преломления. Тогда абсолютный показатель преломления будет определяться по формуле:
n = c / v (5)
где с и v - соответственно скорости света в вакууме и данной среде.
Теория метода.
В данной работе измерение показателей преломления твёрдых веществ производится с помощью микроскопа. При наблюдении предмета через слой воды или через стеклянную пластинку предмет всегда кажется расположенным ближе к наблюдателю, чем в действительности. Это кажущееся приближение связано с преломлением света на границе двух сред и зависит как от толщины пластинки или слоя воды, так и от показателей преломления. Измеряя толщину пластинки с помощью микрометра, а кажущееся смещение предмета при наблюдении сквозь пластинку с помощью микроскопа, тубус которого снабжён микрометрическим винтом, можно определить коэффициент преломления с помощью микроскопа.
Способ 1. Пусть на столике микроскопа лежит плоскопараллельная пластинка толщиной d и микроскоп сфокусирован на пылинки и царапины, находящиеся на нижней поверхности пластинки. Чтобы перефокусировать его с нижней поверхности на верхнюю, тубус необходимо переместить на некоторое расстояние х
(рис.3). Вследствие преломления лучей х < d.


 х
х





 х d
х d
Рис. 3.
Рассмотрим один из лучей, идущих в объектив от метки, находящейся на нижней поверхности пластинки. Из рисунка 3 следует, что
tg / tg = d / х. (6)
Если ограничиться малыми углами наблюдения (объектив микроскопа имеет малый апертурный угол ), то
tg / tg sin / sin = n (7)
и , следовательно,
n = d / х. (8)
Измеряя толщину пластинки d (штангенциркулем или микрометром) и перемещение тубуса микроскопа х при перефокусировке его с верхней поверхности на нижнюю, можно таким образом определить показатель преломления n.
Способ 2. Пусть микроскоп сфокусирован на какой-либо штрих (царапину), нанесённый на предметное стекло. Если положить на предметное стекло стеклянную пластинку толщиной d , то для фокусировки микроскопа на тот же штрих предметного стекла его тубус придётся переместить на некоторое расстояние y (рис. 4).


 у
у










 х d
х d
у
Рис. 4.
Ограничиваясь малыми углами, учитывая, что у = d – х, исходя из формулы (8) можно записать : n = d / d – y (9)
Способ 3. Если для одной и той же пластинки поставить опыты по способам 1 и 2 , то показатель преломления можно вычислить по формуле:
n = 1 + y / х , (10)
которая получена из (8) и (9) путём исключения d.
При измерении показателя преломления изложенными выше способами микроскоп должен удовлетворять следующим условиям:
А) объектив должен быть достаточно длиннофокусным, так как в противном случае окажется невозможным сфокусировать микроскоп на нижнюю поверхность стеклянной пластинки;
Б) объектив должен иметь достаточно малую апертуру. Если это условие невыполнимо, точность измерений существенно снижается из-за ухудшения качества изображения при наблюдении через пластинку;
В) увеличение окуляра следует выбирать , по возможности, большим, чтобы глубина резкости была возможно меньше при фокусировке.
Задание. Измерить с помощью микроскопа показатели преломления трёх различных стеклянных пластин всеми тремя способами и сравнить результаты измерения между собой.
Контрольные вопросы:
Литература.
Изучение законов внешнего фотоэффекта.
Цель: опытным путем проверить законы Столетова и Эйнштейна, определить «красную» границу фотоэффекта, изучить зависимости фототока от интенсивности излучения, приложенного напряжения и от способа освещения фотоэлемента.
Приборы и принадлежности: установка для проведения измерений, нейтральные и цветные светофильтры, фоторезисторы, вакуумный фотоэлемент.
Описание установки:
10






9
8




2
6


4

1
1 – кнопка включения прибора;
2, 4, 6 – цифровое табло, инициирующее силу тока лампы накаливания,
напряжение на фотоприемнике и силу тока фотоприемника соответственно;
3, 5 – ручка регулирования напряжения на лампе накаливания и фотоприемнике соответственно;
7 – кнопка переключения интервалов силы тока;
8 – лампа накаливания;
9 – кассета для светофильтров;
10 – разъем для подключения фотоприемников.
Элементы теории.
Внешним фотоэффектом называется испускание поверхностью тела электронов во внешнее пространство под действием падающего на эту поверхность излучения.
Для изучения фотоэффекта используется вакуумный фотоэлемент F (рис.2).
 I
I
 I нас. ---------
I нас. ---------






К
А
F
мА




Uз 0 U
Рис.2 Рис.3
Этот фотоэлемент включается в цепь источника электрического напряжения. Излучение через прозрачную часть (окно) баллона попадает на катод (К). Испущенные катодом фотоэлектроны под действием электрического поля перемещаются к аноду (А), обеспечивая ток в цепи.
Вольт-амперная характеристика фотоэлемента (рис.3) отражает зависимость силы фототока I от напряжения U при постоянном световом потоке, падающем на катод. При напряжении U = 0 сила тока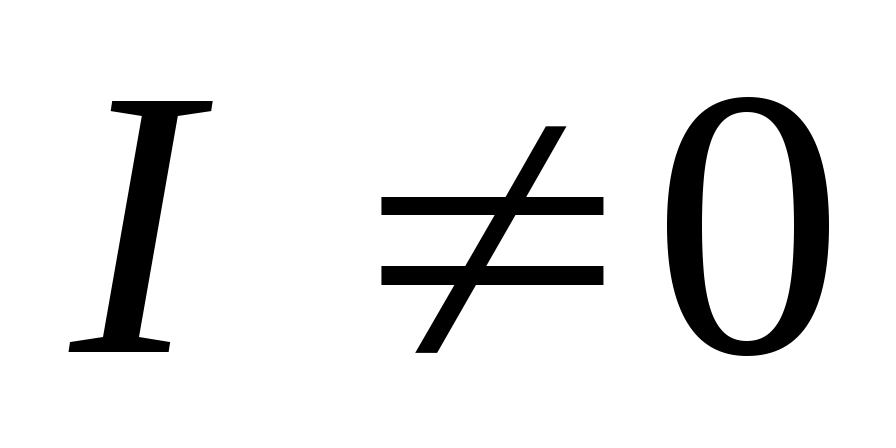 . Это означает, что даже при отсутствии напряжения часть испущенных катодом электроном достигает анода. Для того чтобы сила фототока стала равной нулю, необходимо на электроды подать задерживающее напряжение Uз. Увеличение ускоряющего напряжения приводит к возрастанию фототока, а затем к его насыщению. При насыщении практически все электроны, испущенные катодом, попадают на анод.
. Это означает, что даже при отсутствии напряжения часть испущенных катодом электроном достигает анода. Для того чтобы сила фототока стала равной нулю, необходимо на электроды подать задерживающее напряжение Uз. Увеличение ускоряющего напряжения приводит к возрастанию фототока, а затем к его насыщению. При насыщении практически все электроны, испущенные катодом, попадают на анод.
Внешний фотоэффект характеризуется тремя законами.
Уравнение Эйнштейна, выражающее закон сохранения и превращения энергии при фотоэффекте, имеет вид
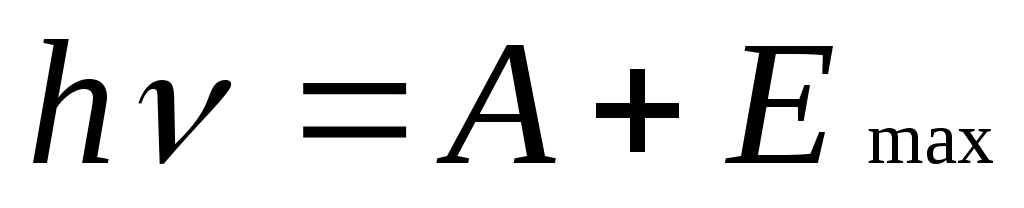 (1)
(1)
где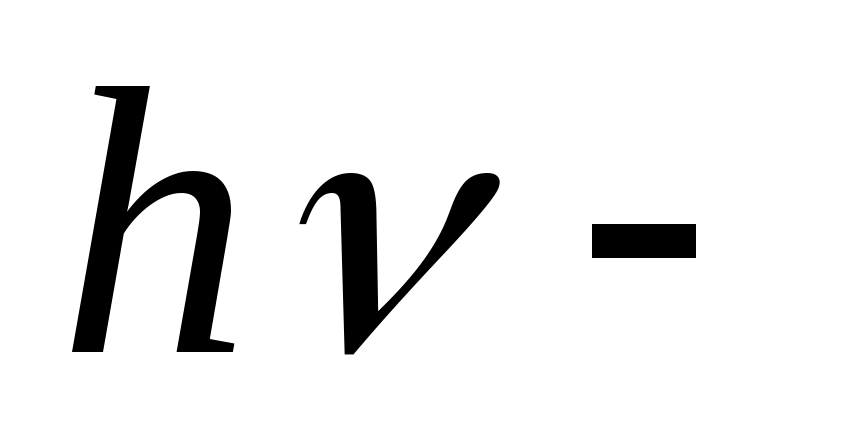 энергия кванта падающего на фотокатод излучения частоты
энергия кванта падающего на фотокатод излучения частоты 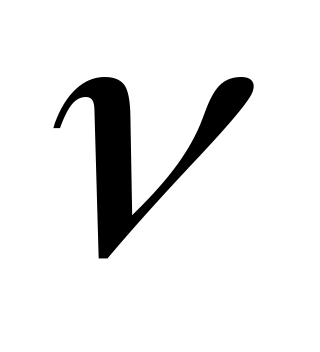 ;
;
h- постоянная Планка; А- работа выхода электрона из материала фотокатода; Emax- максимальная кинетическая энергия вылетевшего электрона.
Электроны в металле обладают разными энергиями – они располагаются на разных энергетических уровнях. Поэтому даже при монохроматическом облучении катода энергия разных фотоэлектронов неодинакова. Работа выхода А характеризует энергию, необходимую для выхода электрона с верхнего заполненного энергетического уровня. Для выхода электрона с ниже расположенных энергетических уровней необходима энергия, большая чем работа выхода А. Кроме того, часть фотоэлектронов теряет энергию при движении из глубины катода к его поверхности. В уравнении (1) под Emax надо понимать кинетическую энергию наиболее быстрых фотоэлектронов.
Из уравнения Эйнштейна следует, что для каждого металла должна существовать некоторая минимальная частота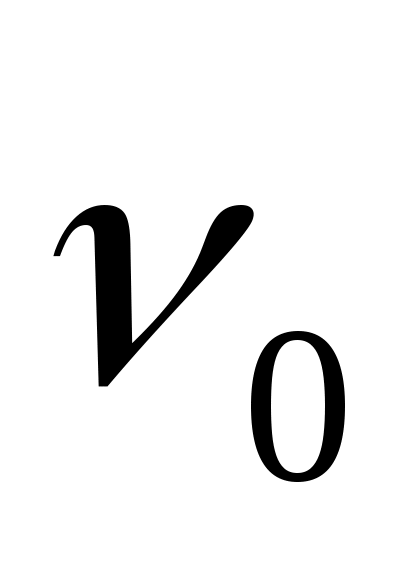 излучения, при которой еще возможен фотоэффект. Это частота, получившая название красной границы фотоэффекта, определяется из (1) при условии Emax = 0 :
излучения, при которой еще возможен фотоэффект. Это частота, получившая название красной границы фотоэффекта, определяется из (1) при условии Emax = 0 :
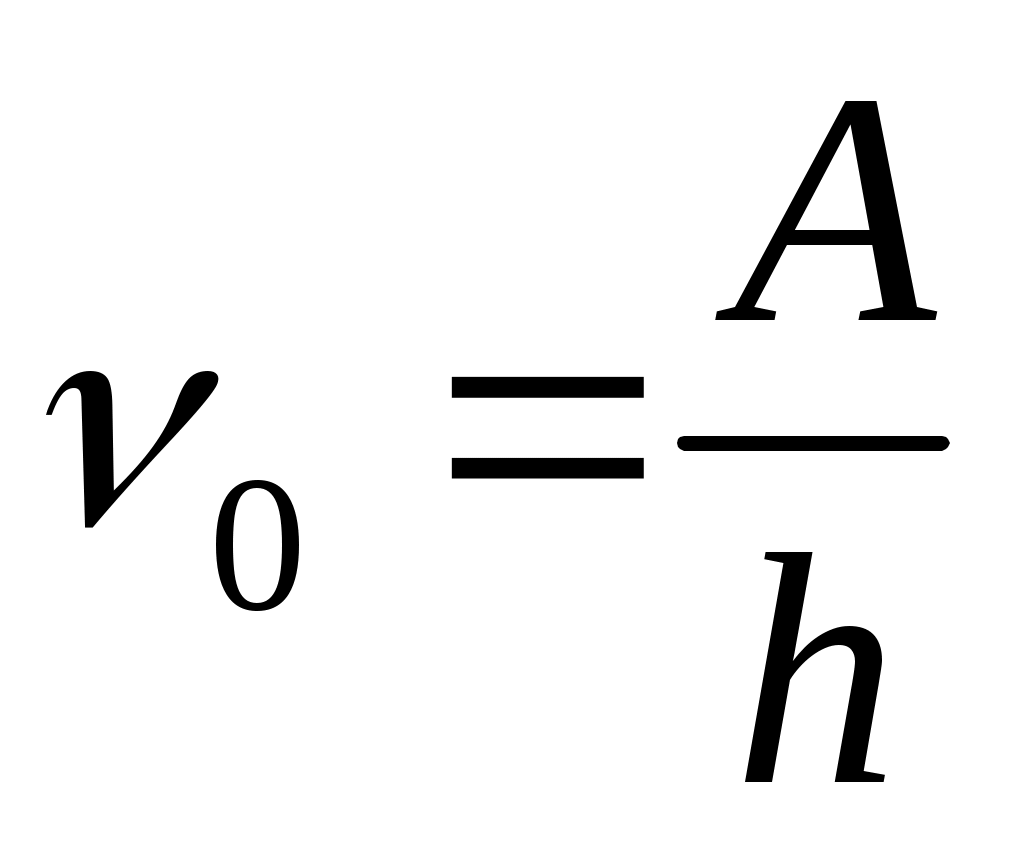 (2)
(2)
ЭнергиюEmax фотоэлектронов можно определить методом задерживающего напряжения. Если на фотоэлемент подать некоторое отрицательное напряжение U, то фотоэлектроны будут тормозиться и электрода А(рис.2) смогут достичь только те электроны, энергия которых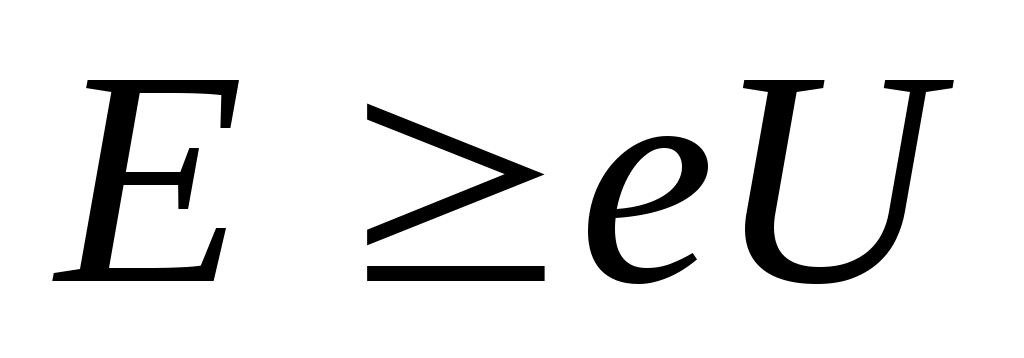 ,где е- заряд электрона. Поэтому анодный ток в цепи уменьшится. При некотором значении задерживающего напряженияUз даже самые быстрые фотоэлектроны не смогут достичь электрода А(рис.2) и анодный ток в цепи прекратится. По закону сохранения энергии
,где е- заряд электрона. Поэтому анодный ток в цепи уменьшится. При некотором значении задерживающего напряженияUз даже самые быстрые фотоэлектроны не смогут достичь электрода А(рис.2) и анодный ток в цепи прекратится. По закону сохранения энергии
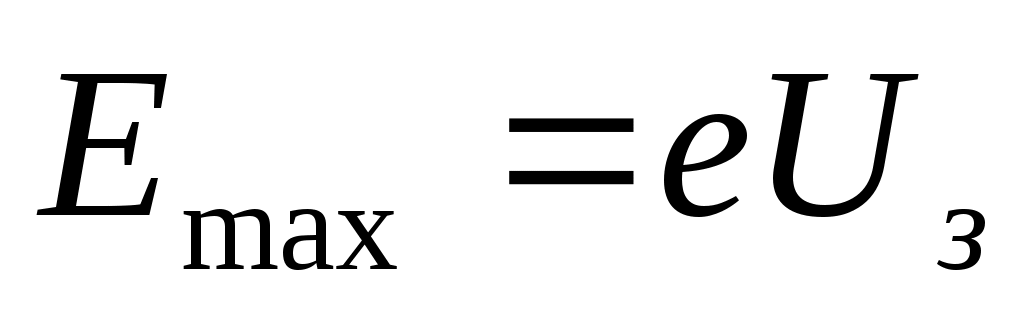 , (3)
, (3)
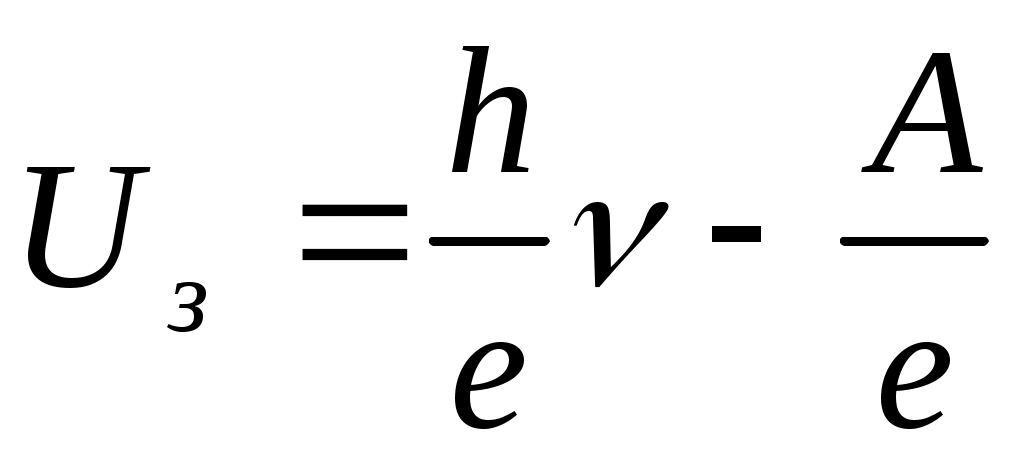 . (4)
. (4)
Задание:
Изучение внешнего фотоэффекта.
В разъем для фотоприемника вставить вакуумный фотоэлемент.
Меняя нейтральные светофильтры, получить разные значения тока насыщения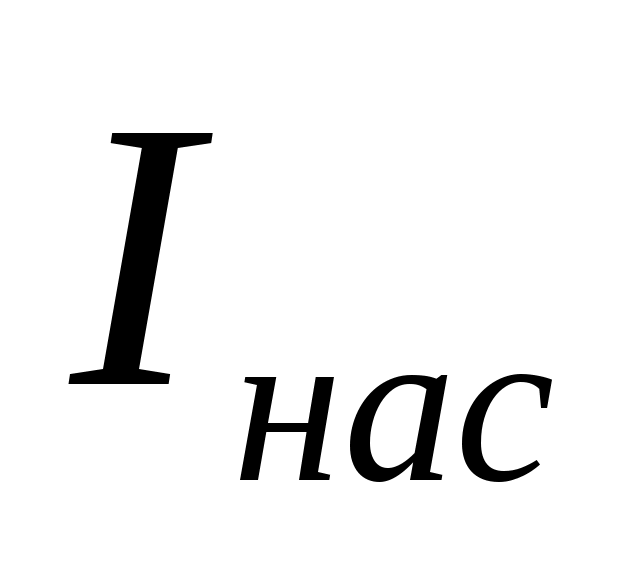 для каждого светофильтра. Результаты измерений занести в таблицу и построить графики зависимостей силы тока Iот напряжения U.
для каждого светофильтра. Результаты измерений занести в таблицу и построить графики зависимостей силы тока Iот напряжения U.
Таблица1
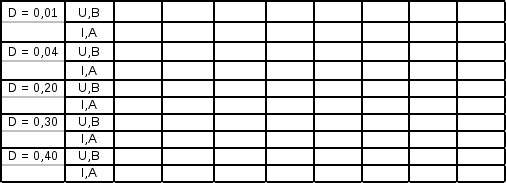
Результаты измерений занести в таблицу 2. Построить график зависимости силы фототока I,mAот длины волны ,нм пропускаемого излучения.
Таблица 2

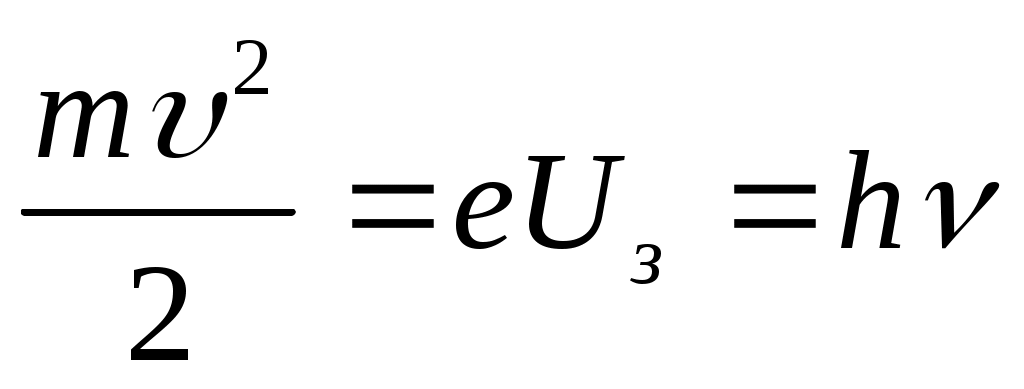
Результаты измерений занести в таблицу 3.
Построить график зависимости максимальной начальной кинетической энергии E



 n1 0 10
n1 0 10n2
Рис. 2.
Для полного отражения фомула (2) будет иметь вид
Sin 0 = n 12 = n 2 / n 1 , n 2 < n 1. (3)
В явлениях преломления и отражения света проявляется взаимодействие света с веществом, в результате чего происходит изменение скорости света. С этой точки зрения , относительный показатель преломления характеризует степень изменения скорости света при переходе его из среды 1 в среду 2, то есть n 12 = v 1 / v 2 (4)
Cоотношение (4) выражает физический смысл относительного показателя преломления. Тогда абсолютный показатель преломления будет определяться по формуле:
n = c / v (5)
где с и v - соответственно скорости света в вакууме и данной среде.
Теория метода.
В данной работе измерение показателей преломления твёрдых веществ производится с помощью микроскопа. При наблюдении предмета через слой воды или через стеклянную пластинку предмет всегда кажется расположенным ближе к наблюдателю, чем в действительности. Это кажущееся приближение связано с преломлением света на границе двух сред и зависит как от толщины пластинки или слоя воды, так и от показателей преломления. Измеряя толщину пластинки с помощью микрометра, а кажущееся смещение предмета при наблюдении сквозь пластинку с помощью микроскопа, тубус которого снабжён микрометрическим винтом, можно определить коэффициент преломления с помощью микроскопа.
Способ 1. Пусть на столике микроскопа лежит плоскопараллельная пластинка толщиной d и микроскоп сфокусирован на пылинки и царапины, находящиеся на нижней поверхности пластинки. Чтобы перефокусировать его с нижней поверхности на верхнюю, тубус необходимо переместить на некоторое расстояние х
(рис.3). Вследствие преломления лучей х < d.


 х
х



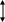

 х d
х d Рис. 3.
Рассмотрим один из лучей, идущих в объектив от метки, находящейся на нижней поверхности пластинки. Из рисунка 3 следует, что
tg / tg = d / х. (6)
Если ограничиться малыми углами наблюдения (объектив микроскопа имеет малый апертурный угол ), то
tg / tg sin / sin = n (7)
и , следовательно,
n = d / х. (8)
Измеряя толщину пластинки d (штангенциркулем или микрометром) и перемещение тубуса микроскопа х при перефокусировке его с верхней поверхности на нижнюю, можно таким образом определить показатель преломления n.
Способ 2. Пусть микроскоп сфокусирован на какой-либо штрих (царапину), нанесённый на предметное стекло. Если положить на предметное стекло стеклянную пластинку толщиной d , то для фокусировки микроскопа на тот же штрих предметного стекла его тубус придётся переместить на некоторое расстояние y (рис. 4).
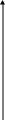


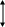
 у
у 









 х d
х d у
Рис. 4.
Ограничиваясь малыми углами, учитывая, что у = d – х, исходя из формулы (8) можно записать : n = d / d – y (9)
Способ 3. Если для одной и той же пластинки поставить опыты по способам 1 и 2 , то показатель преломления можно вычислить по формуле:
n = 1 + y / х , (10)
которая получена из (8) и (9) путём исключения d.
При измерении показателя преломления изложенными выше способами микроскоп должен удовлетворять следующим условиям:
А) объектив должен быть достаточно длиннофокусным, так как в противном случае окажется невозможным сфокусировать микроскоп на нижнюю поверхность стеклянной пластинки;
Б) объектив должен иметь достаточно малую апертуру. Если это условие невыполнимо, точность измерений существенно снижается из-за ухудшения качества изображения при наблюдении через пластинку;
В) увеличение окуляра следует выбирать , по возможности, большим, чтобы глубина резкости была возможно меньше при фокусировке.
Задание. Измерить с помощью микроскопа показатели преломления трёх различных стеклянных пластин всеми тремя способами и сравнить результаты измерения между собой.
Контрольные вопросы:
-
В чём состоит физический смысл абсолютного и относительного показателей преломления? -
Почему объект кажется ближе при рассмотрении его через плоскопараллельную пластинку? -
Чем обеспечивается в микроскопе при экспериментальных наблюдениях малость углов? -
Почему окуляр микроскопа должен иметь большое увеличение?
Литература.
-
Ландсберг Г.С. Оптика. – М.: Наука, 1976, с. 272 –280. -
Поль Р.В. Оптика и атомная физика. – М.: Наука, 1966, с.21–31.
Лабораторная работа№10
Изучение законов внешнего фотоэффекта.
Цель: опытным путем проверить законы Столетова и Эйнштейна, определить «красную» границу фотоэффекта, изучить зависимости фототока от интенсивности излучения, приложенного напряжения и от способа освещения фотоэлемента.
Приборы и принадлежности: установка для проведения измерений, нейтральные и цветные светофильтры, фоторезисторы, вакуумный фотоэлемент.
Описание установки:
10






9
8




2
6


4

1
Рис.1 Схематический рисунок установки
1 – кнопка включения прибора;
2, 4, 6 – цифровое табло, инициирующее силу тока лампы накаливания,
напряжение на фотоприемнике и силу тока фотоприемника соответственно;
3, 5 – ручка регулирования напряжения на лампе накаливания и фотоприемнике соответственно;
7 – кнопка переключения интервалов силы тока;
8 – лампа накаливания;
9 – кассета для светофильтров;
10 – разъем для подключения фотоприемников.
Элементы теории.
Внешним фотоэффектом называется испускание поверхностью тела электронов во внешнее пространство под действием падающего на эту поверхность излучения.
Для изучения фотоэффекта используется вакуумный фотоэлемент F (рис.2).
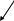
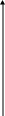 I
I 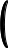
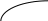 I нас. ---------
I нас. --------- 


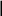


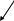

К
А
F
мА




Uз 0 U
Рис.2 Рис.3
Этот фотоэлемент включается в цепь источника электрического напряжения. Излучение через прозрачную часть (окно) баллона попадает на катод (К). Испущенные катодом фотоэлектроны под действием электрического поля перемещаются к аноду (А), обеспечивая ток в цепи.
Вольт-амперная характеристика фотоэлемента (рис.3) отражает зависимость силы фототока I от напряжения U при постоянном световом потоке, падающем на катод. При напряжении U = 0 сила тока
Внешний фотоэффект характеризуется тремя законами.
-
Сила фототока насыщения, а, следовательно, и количество фотоэлектронов, вылетающих в единицу времени с единицы поверхности фотокатода, прямо пропорциональны интенсивности падающего излучения, если его спектральный состав остается неизменным (закон Столетова). -
Скорость фотоэлектронов не зависит от интенсивности падающего излучения. -
Максимальная кинетическая энергия фотоэлектронов линейно возрастает с увеличением частоты монохроматического излучения, вызывающего фотоэффект.
Уравнение Эйнштейна, выражающее закон сохранения и превращения энергии при фотоэффекте, имеет вид
где
h- постоянная Планка; А- работа выхода электрона из материала фотокатода; Emax- максимальная кинетическая энергия вылетевшего электрона.
Электроны в металле обладают разными энергиями – они располагаются на разных энергетических уровнях. Поэтому даже при монохроматическом облучении катода энергия разных фотоэлектронов неодинакова. Работа выхода А характеризует энергию, необходимую для выхода электрона с верхнего заполненного энергетического уровня. Для выхода электрона с ниже расположенных энергетических уровней необходима энергия, большая чем работа выхода А. Кроме того, часть фотоэлектронов теряет энергию при движении из глубины катода к его поверхности. В уравнении (1) под Emax надо понимать кинетическую энергию наиболее быстрых фотоэлектронов.
Из уравнения Эйнштейна следует, что для каждого металла должна существовать некоторая минимальная частота
ЭнергиюEmax фотоэлектронов можно определить методом задерживающего напряжения. Если на фотоэлемент подать некоторое отрицательное напряжение U, то фотоэлектроны будут тормозиться и электрода А(рис.2) смогут достичь только те электроны, энергия которых
Тогда из (1) получаем
Таким образом, задерживающее напряжение Uз линейно зависит от частоты падающего на фотоэлемент излучения.
Задание:
Изучение внешнего фотоэффекта.
В разъем для фотоприемника вставить вакуумный фотоэлемент.
-
В кассету вставить нейтральный светофильтр с наименьшей оптической плотностью D . Не меняя нейтральный светофильтр, увеличить напряжение на электродах фотоэлемента, сила тока при этом должна возрастать. При некотором напряжении она достигнет максимального значения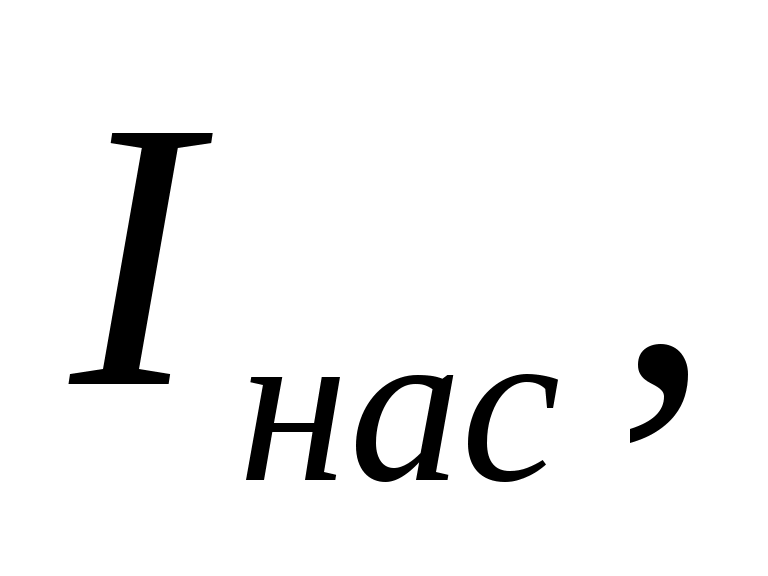 после чего перестанет увеличиваться.
после чего перестанет увеличиваться.
Меняя нейтральные светофильтры, получить разные значения тока насыщения
Таблица1

-
Вставить в кассету фиолетовый светофильтр, подать напряжение на электроды фотоэлемента. Меняя цветные светофильтры в порядке очередности от наименьшей пропускаемой длины волны до наибольшей зафиксировать значение силы фототока. Выбрать светофильтр, при установке которого была зафиксирована наименьшая сила тока, но не равная нулю. Пропускаемое этим светофильтром излучение с длиной волны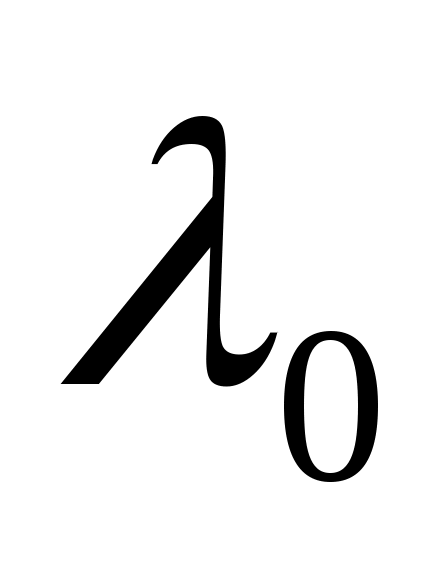 , и будет являться «красной» границей или длинноволновым порогом фотоэффекта.
, и будет являться «красной» границей или длинноволновым порогом фотоэффекта.
Результаты измерений занести в таблицу 2. Построить график зависимости силы фототока I,mAот длины волны ,нм пропускаемого излучения.
Таблица 2

-
Вставить в кассету светофильтр. Изменить полярность фотоэлемента на обратную. При некотором значении напряжения Uз обратной полярности сила тока уменьшится до нуля. Измерив задерживающее напряжение, найти значение максимальной кинетической энергии фотоэлектронов по формуле:
Результаты измерений занести в таблицу 3.
Построить график зависимости максимальной начальной кинетической энергии E