ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 385
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
При скольжениях s << 1, соответствующих холостому ходу и номинальному режиму двигателей, из (9.291) получим
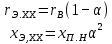
(9.292)Коэффициенты изменения эквивалентных сопротивлений rэ и xэ в зависимости от скольжения
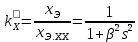; (9.293)
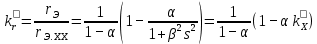(9.294)На основании полученных соотношений и с учетом материала § 9.13 запишем основные расчетные формулы для определения r2 и x2 двухклеточных роторов с общими замыкающими кольцами (двухклеточные роторы с литыми обмотками и роторы с фигурными пазами).
При s0 < s ≤ sн активное сопротивление фазы ротора, Ом,
r2 = rэ.х.х + r0 = rв(1 - α) +
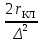(9.295)где α — по (9.290), причем
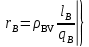(9.296)ρBV, ρHV, lV, lH, qB, qH — удельные сопротивления при расчетной температуре, длины и площади поперечных сечений стержней верхней и нижней клеток; при литых обмотках с общими замыкающими кольцами в ρBV = ρHV и, lV =lH; Δ — см. (9.70).
Индуктивное сопротивление фазы ротора, Ом,
x2 = xп.в + x0 + xэ.х.х, (9.297)
где
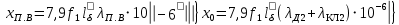(9.298)С учетом (9.298)
х2 =7,9 f1l'δ (λп.в + λп.н α2 + λд2 + λкл2) 10-6, (9.299)
где λп.в, и λп.н — коэффициенты магнитных проводимостей потоков пазового рассеяния соответственно верхней и нижней клеток, которые определяются в зависимости от конфигурации пазов верхней и нижней клеток по формулам табл. 9.34; λд2 — коэффициент магнитной проводимости дифференциального рассеяния ротора, который определяется по (9.180); λкл2 = λл2 — коэффициент магнитной проводимости участков замыкающего кольца, приведенный к току ротора, который определяется по (9.178) или по (9.179).
Для пусковых режимов (s ≥ sн)r2ξ и x2ξ
роторов с общими замыкающими кольцами рассчитывают по следующим формулам.
Активное сопротивление фазы ротора, Ом,
r2ξ = rв(1 – α) k'r +
= rв (1 – α k'x) + (9.300)Таблица 9.34. Расчетные формулы для определения коэффициента магнитной
проводимости пазового рассеянна двухклеточных роторов
и роторов с фигурными пазами
| Рисунок | Расчетные формулы | |
| λП.В | λП.Н | |
| 9.66, а |  |  |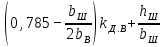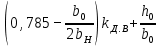
| 9.66, б | |  |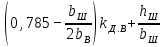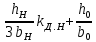
| 9.66, в | |  |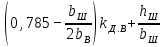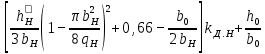
| 9.66, г | | |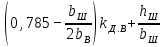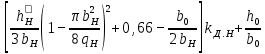
| 9.66, д |  |  |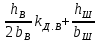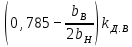
| 9.66, е |  |  |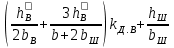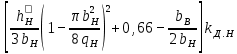
Примечания: 1. При закрытых пазах ротора коэффициент магнитной проводимости шлица hш/ bш рассчитывать в соответствии с указаниями
, приведенными в § 9.10 (см. рис. 9.52).
2. При расчете параметров холостого хода и номинального режима принимать kд.в = kд.н = 1.
Индуктивное сопротивление фазы ротора, Ом,
х2ξ =7,9 f1l'δ (λп.в + λп.н α2k'x + λкл2 + λд) 10-6
В этих формулах k'х и k'r рассчитывают по (9.293) и (9.294), в которых α и β определяют по (9.290), а λп.в и λп.н Для пазов, показанных на рис. 9.66, — по формулам табл. 9.34.
Предполагают, что плотность тока в пределах сечения каждого из стержней постоянна. При ξв > 1 и ξн > 1 можно несколько повысить точность расчета, учитывая влияние эффекта вытеснения тока на сопротивления каждого из стержней. Для этого по формулам, приведенным в § 9.13, последовательно рассчитывают для верхнего стержня ξв, krв, rвξ, kд.в, хвξ и для нижнего стержня ξн, krн, rнξ, kд.н, хп.нξ, после чего определяют
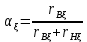
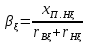(9.302)подставляя эти величины вместо α и β последующие формулы, находят k'хξ и k'rξ и по (9.300) и (9.301) рассчитывают r2ξ и х2ξ с учетом влияния эффекта вытеснения тока на сопротивление каждого из стержней обмотки при принятых значениях s. Обычно krв и krн близки к единице, и уточнения расчета, связанного с влиянием эффекта вытеснения тока на каждый из стержней, не требуется.
Для уточнения расчета пускового момента и тока следует учесть также влияние насыщения от полей рассеяния на проводимость паза верхней клетки. Расчет проводят аналогично изложенному в § 9.13.
При расчете сопротивлений роторов с раздельными замыкающими кольцами (двухклеточные роторы с обмоткой из вставных стержней) аналогично принятому ранее допущению (хв.н = хп.в) принимают, что индуктивное сопротивление участков замыкающего кольца верхней клетки приблизительно равно сопротивлению и взаимоиндуктивности участков колец верхней и нижней клеток. Такое допущение позволяет использовать ту же схему замещения (см. рис. 9.65), но с несколько измененными значениями ее параметров. В схеме замещения ротора с раздельными кольцами:
сумма активных сопротивлений стержня и участков замыкающих колец верхней клетки
Rв = rв
+
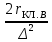(9.303)сумма активных сопротивлений стержня и участков замыкающих колец нижней клетки
Rн = rн +
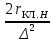(9.304)сумма индуктивных сопротивлений пазового рассеяния и участков замыкающих колец верхней клетки
хв = хп.в + хкл.в = 7,9 f1l'δ (λп.в + λкл .в)10 -6 ; (9.305)
сумма индуктивных сопротивлений пазового рассеяния и участков замыкающих колец нижней клетки
хн = хп.н + хкл.н =7,9 f1l'δ (λп.н + λкл .н)10 -6 . (9.306)
В этих выражениях λп.в и λп.н — коэффициенты магнитной проводимости пазового рассеяния соответственно верхней и нижней клеток (рассчитываются в зависимости от конфигурации пазов по данным табл. 9.33); λкл.в, λкл.н — коэффициенты магнитной проводимости участков замыкающих колец [рассчитываются по (9.178) или (9.179)].
Общее сопротивление для обеих параллельных ветвей схемы замещения
z0 = х0 = хд = 7,9 f1l'δ λД 10 -6., (9.307)
где λд — коэффициент магнитной проводимости дифференциального рассеяния, рассчитываемый по (9.180).
Сопротивления r2 и х2 роторов с раздельными замыкающими кольцами для холостого хода и номинального режима работы, Ом,
r2 = rэ.х.х = Rв (1 – α); (9.308)
х2 = хв + хэ.х.х + х0 =7,9 f1 l'δ (λп.в + λп.нα2 + λкл.в + λд) 10-6 , (9.309)
где
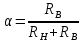
Сопротивления r2ξ и x2ξ, для пусковых режимов работы (s >> sн), Ом,
r2ξ = rэ = Rв (1 – αk'х); (9.310)
х2ξ = 7,9
f1l'δ (λп.в + λп.н α2k'x + λкл.в + λд) 10-6, (9.311)
где k'x определяется по (9.293) при
β = Хн / (Rв + Rн). (9.312)
Эффект вытеснения тока в каждом из стержней и влияние насыщения полями рассеяния на параметры ротора учитывают так же, как и для роторов с общими замыкающими кольцами.
Приведенный метод расчета параметров двухклеточных роторов и роторов с фигурными пазами, как и другие аналогичные ему методы, учитывающие индуктивную связь только между полными токами каждого из стержней, являются приближенными, однако они находят применение в расчетной практике благодаря своей простоте. Более точный метод расчета параметров ротора с произвольной конфигурацией стержней рассматривается в спецкурсах [7].
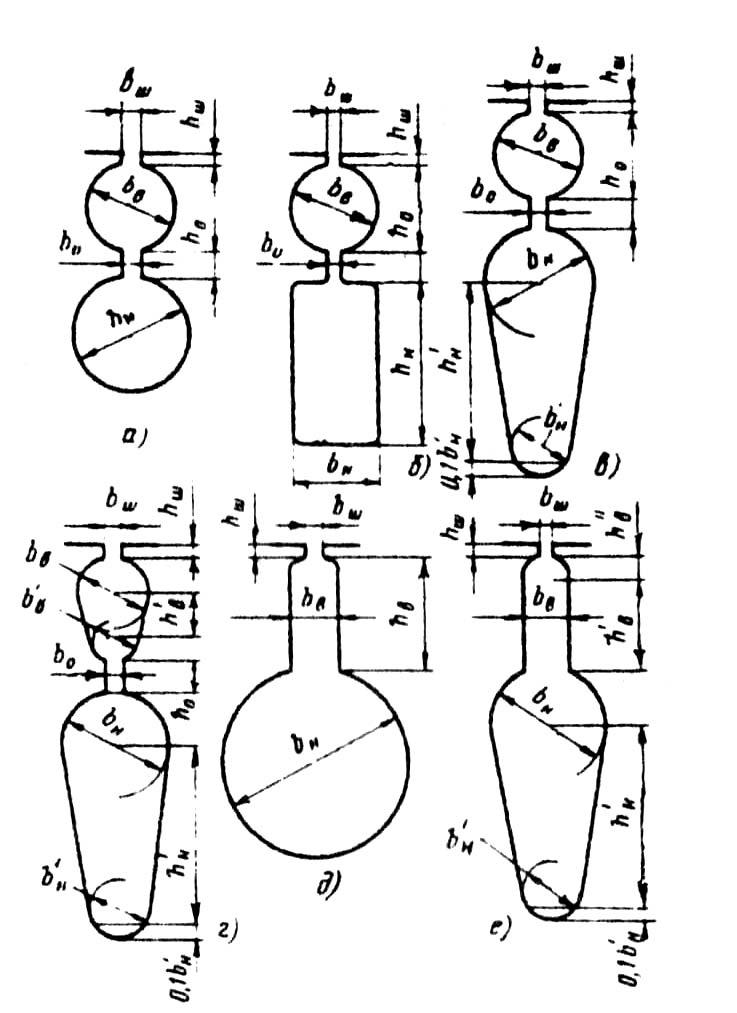
Рис. 9.66. К расчету коэффициентов магнитной
проводимости пазового рассеяния двухклеточных
короткозамкнутых роторов с двойной беличьей клеткой
и с фигурными пазами:
а—г — пазы роторов с двойной беличьей клеткой;
д, е — фигурные пазы
9.15. ОСОБЕННОСТИ ТЕПЛОВОГО И ВЕНТИЛЯЦИОННОГО
РАСЧЕТОВ АСИНХРОННЫХ ДВИГАТЕЛЕЙ
На первоначальной стадии проектирования достаточно достоверную оценку теплового режима двигателя дает приближенный метод теплового расчета, основанный на упрощенном представлении о характере тепловых связей между элементами электрической машины. В нем используют средние значения коэффициентов теплоотдачи с поверхности и теплопроводности изоляции, характерные для определенной конструкции и технологии производства двигателей данного типа.
Для расчета нагрева асинхронных машин, спроектированных на базе серий 4А и АИ, берутся усредненные коэффициенты теплоотдачи с поверхности и теплопроводности изоляции в пазовой и лобовой частях обмоток.
Расчет нагрева проводят, используя значения потерь, полученных для номинального режима, но потери в изолированных обмотках статора и фазного ротора несколько увеличивают по сравнению с расчетными, предполагая, что обмотки могут быть нагреты до предельно допустимой для принятого класса изоляции температуры: при классе нагревостойкости изоляции В — до 120° С, при классе нагревостойкости изоляции F — до 140° С и при классе нагревостойкости изоляции Н — до 165° С. При этом коэффициент увеличения потерь k